Autor : Carlos Bechara.

Análisis de los frentes de onda en la reflexión de la luz

En la clase anterior habíamos dejado en claro, que cualquier teoría era relativa y solo válida para ejemplificar ciertas cuestiones, también habíamos dicho que la teoría ondulatoria era muy útil para analizar el comportamiento de los haces luminosos en un sistema óptico cualquiera, tanto por ser el que más se acerca a la realidad (ya que se piensa en tridimensión), como por ser el que mejor se adapta a los problemas de la óptica aplicada a la iluminación o mejor, a la luminotecnia.

En principio vamos a la teoría, pero teniendo en cuenta que todos los principios que desarrollemos en esta edición se resolverán en forma práctica en la próxima ficha, así que un poco de paciencia y atenta la neurona que ahí va.

Principio de reflexión

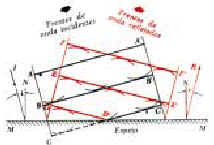
Consideremos un frente de onda plano A A’ (siempre pensando que es como una sección de una esfera: tridimesional aunque el gráfico correspondiente sea bidimensional); que se dirige hacia un espejo plano M M’ (fig. 1). La aplicación del principio de Huyghens conduce al frente de onda B B’. Siguiendo la misma construcción, debemos presuponer que el próximo frente: C C’ se encontrará parcialmente por encima del espejo y otra parte por debajo del mismo. A simple sentido común sabemos que esto no es posible, puesto que la luz no puede atravesar un cuerpo opaco. La ondulación que debería encontrarse debajo del espejo deberá invertir su curvatura, dando lugar a un frente de onda quebrado, D D’C’. El frente de onda siguiente E E’ puede trazarse mediante la misma construcción.

En el diagrama, "I" representa el rayo incidente (o sea, el sentido de propagación de los frentes de onda incidentes); "R" es el rayo reflejado, o sentido de propagación de los frentes reflejados. Como ya sabemos el ángulo de incidencia "i" es igual al ángulo de reflexión "r", y "N" son las normales.

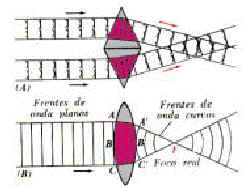
Veamos ahora el efecto de un espejo curvo sobre un conjunto de frentes de onda de luz. Supongamos (Fig. 2 A), una serie de frentes planos procedentes de una fuente lejana que se dirigen hacia un espejo esférico cóncavo. Obsérvese que los extremos superior e inferior de cada frente de onda se encuentran o "chocan" con el espejo antes de que el punto medio entre en contacto con la superficie del espejo.

Resulta entonces que las ondulaciones secundarias procedentes de los extremos de cada frente invierten inmediatamente su sentido, mientras el centro sigue sin variación. Las envolventes de las ondas reflejadas toman mayor curvatura que la propia del espejo y obviamente mucho más que la correspondiente a los frentes de ondas incidentes, que habíamos supuesto nula.

La inversión de la curvatura de los frentes de onda incidentes da a lugar a una imagen real de la fuente distante situada en el foco del espejo esférico.

Veamos qué ocurre situando la fuente luminosa muy próxima al espejo cóncavo de modo que el punto P (objeto) quede a una distancia menor a al distancia focal del espejo (Fig 2B).

En la figura 2B se ve una serie sucesiva de frentes de onda de pronunciada curvatura (debido a lo cercano de la fuente luminosa) que se dirigen hacia el espejo desde el punto P.  El extremo inferior del frente entra en contacto en primer lugar con el espejo y sus ondulaciones experimentan inmediatamente su inversión; el extremo superior del mismo frente, todavía continua propagándose sin variación. El frente de onda invierte luego el  sentido de propagación (se refleja) al invertirse la curvatura y el sentido de propagación . El haz reflejado es divergente y sale del espejo como si proviniera de un punto Q situado detrás del mismo, que es la imagen virtual de la fuente luminosa .

Vamos a parar un minuto para seguir insistiendo en el tema de los códigos de representación, estos gráficos no son más que una representacion abstracta (en bidimensión) de un hecho concreto y tridimensional; solo de esta manera se puede tomar conciencia del hecho físico en si. Por otra parte, el espejo curvo podría ser desarrollado como un espejo curvo-plano, como el de un reflector de cuarzo, o bien, como un espejo cóncavo esférico (esferoide de revolución) como el que se utiliza normalmente en la construcción de un proyector con lente plano convexa o Fresnel.

Un frente de onda es como una porción de una esfera tridimensional en una sucesión o "tren" de frentes y se vuelven planas al estar la fuente de emisión muy lejana, en el segundo gráfico esta fuente (P) podría muy bien ser una lámpara cercana a un espejo; en ese caso debemos entender que la porción utilizada para graficar el ejemplo es solo una ínfima parte de la luz que emitiría una lámpara de cualquier tipo en esa posición particular. Más adelante desarrollaremos estos conceptos en ejemplos concretos de la propia construcción de las luminarias teatrales.

Principio de refracción

Vamos a recurrir ahora al principio de Huyghens para estudiar los frentes de onda de luz al pasar a través de prismas y lentes. En la figura 3A , se ve la trayectoria de dos grupos paralelos de frentes de onda planos que atraviesan dos prismas triangulares unidos por la base.

Obsérvese el retraso progresivo de los frentes de onda (o contracción de la longitud de  onda) a medida que la luz penetra en un cuerpo en el cual su velocidad es igual a C/n ("n" es  el índice de refracción). Veamos también el adelanto de los frentes de onda, a medida que la luz vuelve al medio en el cual su velocidad es igual a "C" . La variación en diferentes puntos de los frentes de onda, trae aparejada la refracción. o sea, la modificación de la trayectoria de los haces luminosos.

Si bien ambos haces se reúnen, no lo hacen concurriendo en un punto o foco debido a la forma geométrica del elemento refractor.

En cambio en la figura 3B tenemos una lente biconvexa, más adecuada a nuestros fines, se ve un frente de onda plano ABC , entrando en contacto con la lente en el punto B. Como el centro y los extremos del frente de onda se retrasan y adelantan en proporción diferente a medida que la luz entra y sale de ella, el frente de onda emergente A’ B’ C’ resulta notablemente curvado y convergente. Al doblar los extremos de los frentes hacia adentro, la lente convergente concentra la luz en un punto o foco "F".

Es tentador decir que entonces si situamos en el punto F una lámpara, invirtiendo el sentido de propagación, obtenemos el principio de un proyector de frentes de ondas planos, o sea un proyector capaz de emitir rayos paralelos, pero eso ya es otra historia.

Analicemos ahora la figura 4 A. que hace resaltar el hecho de que los refractores (lentes), como los reflectores (espejos), pueden hacer variar la magnitud y el sentido de curvatura de los frentes de onda incidentes.

En el caso representado, el proceso de retraso y adelanto diferencial, al verificarse en diferentes puntos de los frentes de onda, hace disminuir su curvatura dentro de la lente, invirtiéndola además.

Los frentes de onda emergentes tienen menor grado de curvatura que los incidentes y se concentran en un punto "Q" , imagen real de un objeto situado en "P".

En la próxima clase vamos a hacer una pausa en la teoría para ver cómo se transforman estos principios de la óptica geométrica en elementos concretos.

Antes de seguir avanzando y meternos en terrenos un poco más dificultosos , afirmemos estos conocimientos revisando el material que tenemos en el taller, así que que hasta la próxima

…y traigan herramientas.