Autor : Carlos Bechara.

En esta entrega vamos a empezar a incorporar la teoría de la óptica en óptica aplicada, habíamos quedado en revisar el taller. Quiero suponer que por lo menos encontraron una PAR 64 (o sea una Par mil en criollo) y ésta era (por casualidad) una very narrow , las que dicen VNSP atrás y son transparentes adelante. Sí? Bárbaro, ahora la sacamos del artefacto y llevamos la lámpara y el artefacto a un lugar cómodo; prendemos un cigarrillo y vemos que hay.

Empezamos por revisar el artefacto, digamos que es del tipo Thomas de cualquier marca nacional, de aluminio (negro o plateado, es igual); tiene en su horquilla una agarradera para ajustar, tres o cuatro sujetadores para el portafiltro, se puede abrir en dos partes con un mecanismo simple.

En la parte de ‘adelante’ tiene una rejilla de protección, está se debería encontrar siempre, es una medida de seguridad (por si la lampara estalla), que no permite que pedazos de vidrio grandes caigan desde el artefacto. Esto es muy improbable pero puede pasar. Sigamos.

Encontramos un "zuncho" de metal para sujetar la lámpara por detrás, pero permitiendo girarla sin dificultad (nada raro), y en la parte de "atrás" encontramos la parte de conexión eléctrica, con su zócalo de cerámica (muy bueno para poder maniobrar la lámpara sin problemas), un prensacable, conexión a tierra, y no hay mas nada!!! No tiene nada: ni mecanismos, ni lentes, nada. Es un simple "contenedor" de una lámpara.

...así que el chiste debe estar en la lámpara. (Fig. Nº 1 .)

Entonces veamos la lámpara. Aclaremos que la denominación de PAR corresponde a la sigla Parabolic Aluminized Reflector en ingles y simplemente describe el carácter general de estas lámparas, o sea, que están compuestas por una "ampolla", lámpara por supuesto halógena, que contiene un filamento con su conexión eléctrico-mecánica y todo encerrado en una "unidad sellada" compuesta de una cara frontal (en este caso transparente) y una cara posterior en donde se encuentra el reflector.

Veamos primero el material del reflector: es una superficie cóncava de cristal térmico, cubierta por dentro con una capa como "azogada" de material de aluminio de tal calidad que se comporta como un espejo capaz de reproducir imágenes, es decir, con la obvia distorsión de un espejo curvo "nos podemos ver la cara". No es una simple superficie pulida. Eso por una parte nos asegura una excelente capacidad de reflexión, pero que pasa con la posible reproducción de imágenes, que en este caso no nos interesa para nada.

Todos sabemos por experiencia que una VNSP reproduce en cierto modo la disposición del filamento como una "línea caliente" sobre el piso de un escenario. Entonces, para entender todo esto, debemos analizar ópticamente cómo funciona un espejo parabólico cualquiera, para compararlo luego con nuestra lámpara en particular. Fig. Nº 2

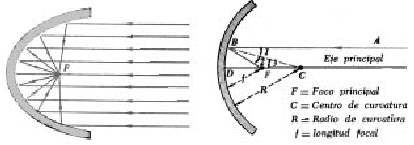
En esté gráfico vemos un corte de un espejo parabólico y muestra una sección transversal de los rayos paralelos, que corresponde a una onda plana E que incide sobre un espejo M . Los rayos reflejados convergen en el punto F . Las longitudes de trayectoria óptica de todos los caminos que van a F deben ser las mismas.

Por ejemplo si AB + BF es 9 cm. debería ser igual a EG + GF y así con cada LTO.

Ahora supongamos que los segmentos lineales AB , EG,….XY se prolongan mas allá del espejo hasta los puntos C, H,….Z , que se escogen de manera que:

BC = BF , GH = GF , …. , YZ = YF

Los anteriores conjuntos de igualdades implican que

AB + BC = EG + GH = ……XY + Yz

Lo cual dice que la distancia entre E y la línea E` que pasa por los puntos C, H …, Z es constante. Se construye así una recta E` tal que los puntos de M son equidistantes de ella y del punto F .

Por consecuencia y definición, entonces, M es una parábola con foco en F y directriz en E`. Esto se demuestra por el principio de Fermat sobre las longitudes de trayectoria óptica (LTO) ver gráfico Nº3.

Los rayos de Sa Patravesarán presumiblemente un gran número de trayectorias diferentes a través del sistema. Supóngase que una de tales trayectorias corresponde a la mínima L.T.O. entre Sy P. El principio de Fermat enuncia que la luz atravesará ese camino de mínima L.T.O. y ningún otro. Los rayos seguirán otros caminos puesto que dejan S en muchas direcciones. Se deduce que esa L.T.O. mínima (o máxima), no puede ser la única alcanzada. En otras palabras, todos los rayos de S que atraviesan el sistema hasta P deben atravesar longitudes de trayectoria óptica idénticas. Esto se cumple para toda clase de sistemas enfocados (tales como lentes y espejos).

Con esto, resulta tentador el pensar simplemente que una lámpara ubicada en el foco de una parábola bastaría para que todos los rayos reflejados sean paralelos y listo.

Ya tenemos una PAR comprendida, pero no, ...faltan un par de detalles muy importantes: Primero consideremos qué pasa con la geometría de una parábola y veamos cuál es la relación de ésta con respecto a la ubicación del filamento de la lámpara, con respecto a la focal del espejo.

En este gráfico se pone en evidencia que una parábola comparte en su curva una coincidencia concreta con la curva de un espejo esférico.

Si tenemos en cuenta la aberración esférica de esta parte del espejo y a eso le sumamos que el filamento de una PAR es mucho más grande que un punto exactamente geométrico ya estamos en problemas.

Si además entendemos que en cualquier caso, lo que emite una lámpara PAR es la resultante de la luz "recuperada" más la emisión del filamento o la luz "directa", estamos en graves problemas.

Entonces terminemos de definir cómo funciona una lámpara de PAR 64 , en este caso una VNSP.

Ya sabemos que es una unidad sellada que contiene una lámpara halógena de 1000 Watts , 3.200 º Kelvin de temperatura de color, que puede ser de 110 0 220 Volts según su origen y/o marca, y ópticamente esta lámpara se encuentra en un punto de equilibrio entre el foco real del espejo parabólico y el punto anterior al de aberración esférica. La parábola del espejo reflector es un paraboloide de revolución, y su función de curvatura responde a las características de una parábola muy abierta. De hecho podemos afirmar que si analizamos el comportamiento de los frentes de onda reflejados veremos que una curva abierta produce un cruce de haces en el espacio menor que el de una parábola de curva mas cerrada.

A este cruce se le suma el haz de luz directa divergente, que es contenido por el artefacto en el que se la instala. El rendimiento total de un artefacto con una PAR 64 VNSP debe considerarse en estos términos de sumatoria y es fácilmente perceptible sin necesidad de instrumentos.

Como prueba práctica, pueden dimerizar dos lámparas de las mismas características: una al aire y otra dentro de un artefacto y con un poco de humo más o menos parejo... y observar qué pasa con la propagación de la emisión de esta lámpara proyectando su haz sobre una pared a unos cinco metros.

Ojo!, que básicamente hay dos tipos de construcción de filamentos: el más común está dispuesto longitudinalmente con respecto a la cara del reflector y es el que produce un haz más ovalado, y el filamento tipo parrilla puesto axialmente a la cara del reflector y que produce un haz un poco mas circular.

Bueno, por ahora es suficiente. Les dejo unos deberes: ya que están en el taller, revisen y comparen esta lámpara con respecto a las Narrow y las Medium Flood, a ver qué conclusiones sacan.