Autor : Carlos Bechara.

En la clase Nº 6 habíamos demostrado qué es lo que sucedía en una lente de un proyector Plano Convexo (PC) mediante la ya conocida Teoría de los Frentes de Onda de Huyghens y las partes constructivas más o menos históricas de estas luminarias, pero bueno, ya que tenemos desarmado un Plano Convexo o varios, concentremos la atención en la lente en sí misma, para ampliar ópticamente el concepto de utilización de ésta.

Ya habíamos dicho que están construidas en vidrio Crownglass templado, con un índice de refracción práctico de 1,5 y digamos que es además una lente "positiva" y convergente, que por tener una cara plana y una esférica tiene características particulares dentro de las lentes positivas.

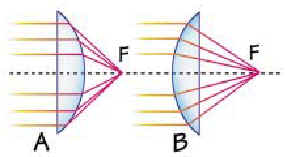
Sabemos que una lente es positiva si cumple con la condición de los " focos convergentes". FIG 1

Tomamos por ejemplo el caso A y vemos un haz colimado (paralelo) entrando a la cara plana perpendicularmente, el desvío de los rayos ocurrirá en su totalidad en la cara curva demostrando uno de los planos principales siempre será tangente a la superficie curva y en el caso B se observa el mismo efecto.

Analíticamente se puede demostrar que en una lente Plano Convexa la focal es independiente de su espesor puesto que según la formula de las lente gruesas:

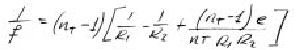Al tener uno de los radios R1 O R2 = infinito, la dependencia de "e" desaparece. Ahora bien esto es "teoría". En luminotecnia, el espesor es vital pues de él depende el factor de pérdida por transmisión en el caso de proyectores de luz y la aberración esférica en el caso de producción de imágenes. También es evidente que al ser R1=infinito y un valor estándar de "n" (índice de refracción) se puede despejar de la fórmula anterior, una más sencilla fórmula de la focal de una lente plano convexa que es: f = 2 x R2 o en otros términos: f=2 x Rc siendo Rc el radio de curvatura de la cara curva. (fig.3)

Sea que podemos asegurar que en una lente plano convexa "la focal será igual al doble del radio de curvatura de la única cara curva y será tomada desde el vértice de ésta".

Pero como estamos en el taller, veamos cómo podemos mensurar de una manera más práctica la lente que tenemos entre manos, si es que todavía no la revoleamos para la calle. El problema principal es cómo medir un radio de curvatura sin elementos adecuados.

Se puede medir el diámetro con una regla milimetrada, el espesor tampoco es problema, pero hay que pasar luego estas medidas en escala a un papel y con un compás tratar de "embocar" a prueba y error la curvatura correcta. Hay que armarse de mucha paciencia y se puede lograr un resultado bastante aceptable, con un margen de error que para el tipo de medición que nos importa es despreciable, por ejemplo, si por gráfica la focal les da 302mm., pónganle la firma que es 30cm. y todo bien.

¡Pero no asustarse! hay una forma mas fácil. Siéntense en la mesa de trabajo, corran el mate, prendan un pucho y relájense; pongan una hoja de papel blanco que quede lo más perpendicular posible a la luz que incida sobre la mesa.

Supongamos que a un par de metros tienen una lámpara incandescente. Tomen la lente con la cara plana hacia la lámpara y busquen, como cuando eran chicos y jugaban con una lupa a enfocar el sol para encender un papel (se acuerdan?). Cuando vean la "forma" puntual del filamento, midan esa distancia de la cara curva al papel y ESA es la focal.

De paso hagan la prueba y denle una mayor distancia del papel y van a ver como se reproduce en forma invertida la imagen de la lámpara y acaban ustedes de descubrir el principio de la proyección de imágenes usando como "objetivo" una simple lente plano convexa.

De todo esto se deduce fácilmente que para la proyección de luz que se desea obtener de un proyector plano convexo, la distancia del "objeto" (lámpara) debe ser menor al valor de la distancia focal de la lente, rango en el cual la imagen es virtual ya que, al llegar al caso de So (distancia objeto) = a focal, la imagen se convertirá en "real". Cuántas veces les pasó que, al achicar el rayo de un PC, la forma circular se va haciendo cada vez más cuadrada hasta aparecer claramente la forma de la parrilla del filamento? Es muy probable que esa lente no sea la que corresponde al artefacto y si no es así, ya saben qué marca no hay que comprar. Ojo, que el caso contrario no es mucho mejor.

Suele pasar que algún despistado ponga una lente plano convexa en un artefacto para lente fresnel (que tiene un recorrido mucho menor) y ese artefacto obviamente va a abrir mucho pero no va a cerrar lo suficiente.

Bueno creo que para una jornada es suficiente, pero si tienen ganas de entretenerse les dejo unos "deberes" para ir pensando.

Ya vimos cómo, por defecto, una lente plano convexa produce imágenes "indeseables", pero qué pasa cuando la usamos adrede?

Prueben. Por ejemplo: busquen un PC que achique lo más posible. Pónganle un portafiltro con un color estropeado o perforado o escriban algo con un fibrón sobre el filtro, enfóquenlo sobre una pared y ahora tomen otra lente plano convexa sosteniéndola alineada adelante del proyector. Cuando lleguen a la focal de la lente que sostienen en la mano, verán sobre la pared la imagen invertida del filtro hasta el menor detalle.

Acaban de descubrir el principio de cualquier proyección!

Después, si tienen la posibilidad, revisen los sistemas ópticos de proyecciones, elipsoidales, si usan una lente o más, de qué tipo, en qué orden, si están enfrentadas, seguidas,... investiguen!

Y si no, la próxima les cuento.