Autor:  Ing. Alejandro Bidondo

Hasta ahora hemos hablado de sistemas, usos, algo de sentido común, temas que estudiar (los que presupongo ya han leído), etc., y puedo afirmar que ni siquiera hemos ingresado en el "prólogo" del estudio formal del sonido, pero nos falta, para continuar la introducción, hablar algo de la señal que contiene la información sonora. 

Aquí debemos definir algunos conceptos:

Señal:  es aquella variación en función del tiempo de un parámetro físico. Podemos encontrar variaciones, o sea señales, de presión, humedad, luz, calor, energía, velocidad, caudal, concentración, etc., etc.. Toda señal lleva consigo (o transporta desde un emisor hasta un receptor) cierta cantidad de información.

 La cantidad de información es el recíproco de la probabilidad de un evento (posibilidad de ocurrencia). O sea que cuanto menos probable sea, mayor cantidad de información contiene dicha señal. 

La probabilidad  es una magnitud adimensional que varía desde cero hasta uno, en forma continua. Si se la multiplica por 100 el resultado expresa el porcentaje de ocurrencia.

Es muy importante tener en cuenta que la misma está restringida por el ancho de banda del canal y por la potencia de ruido existente. Esto se aplica directamente al caso de reducir el slew rate de las señales, ya sea por un mal microfoneo o por utilización de dispositivos electrónicos, viéndose mermada la información y el ancho de banda de la misma.

La señal que transporta información sonora pasa por varios dominios, antes de ser percibida por una persona, a saber (genéricamente):

• Mecánico o electrónico, según el tipo de fuente, a la hora de ser generada.

• Acústico, al ser emitida del instrumento o del transductor electroacústico y entra en contacto con el aire (en el caso de que el medio de propagación de la onda sonora sea el aire). 

• Eléctrico o Electrónico, al ser transducida por micrófonos o generada directamente en forma electrónica, para poder ser transportada y procesada por consolas mezcladoras, compresores, efectos artificiales, amplificadores, etc. Este tipo de señal es la llamada señal de audio.

Estas señales, si bien difieren de dominios, poseen ciertas características a partir de las cuales pueden ser estudiadas, analizadas y comparadas.

Parámetros y funciones en el dominio de las magnitudes

Una señal es estacionaria si algunas de sus propiedades promedio (por ejemplo: energía en función del tiempo) no varían al transcurrir el tiempo. Pueden ser señales tanto determinísticas como aleatorias, por ejemplo una señal periódica cualquiera.

Las características de las señales en el dominio de las magnitudes están limitadas generalmente a aquellas que son estacionarias.

Valor medio y rms (root mean square)

Dada una señal estacionaria x(t), se pueden obtener diferentes valores promedio llamados (estadísticamente) "momentos". Los de mayor interés son:

• m1: Valor medio.

• ss: Desvío estándard.

• Ys: Valor rms (root mean square).

Estos valores se definen como:

T es el tiempo lineal de promediación. Las tres cantidades están relacionadas de la siguiente manera:

Es decir, cualesquiera dos cantidades, definen a la tercera. El valor medio define la tendencia central de la señal. La desviación estándar define la dispersión respecto de su valor central. El valor rms es función tanto de la tendencia central como de la dispersión. Cada magnitud tiene por unidad la misma que la de la señal en cuestión.

Aplicaciones

- En la mayoría de las mediciones acústicas el transductor no sensa la componente estática o componente de continua (DC). En estos casos el valor medio de la señal es cero y el valor rms es igual a la desviación estándard.

- Una señal senoidal pura (y(t)= A sen (t + Q ) posee un valor medio y rms determinados por su ecuación característica, pero si bien es una (famosa) señal utilizada para pruebas de audio, es completamente inservible para pruebas psicoacústicas, necesitando en ese caso señales tipo música, palabra o simplemente ruido ya sea de banda angosta, filtrado, modulado, etc..

Funciones en el dominio del Tiempo

La relación lineal entre dos valores de una señal en dos instantes de tiempo dados (t y t+ ) está dada por la función de autocorrelación, Rxx.

Para una señal determinística esta relación puede ser resuelta directamente de la ecuación que la define, pero para una señal estacionaria y aleatoria esta relación lineal está definida por la siguiente ecuación: 

En las siguientes figuras observamos una señal x(t) de banda ancha y aleatoria, y su función de autocorrelación Rxx, la cual nos informa que sólo existe una relación lineal alta cuando t=0, o sea cuando los dos instantes son el mismo instante; el resto de los instantes tienen una correlación muy baja entre sí confirmándonos que es una señal tipo ruido.

Aplicaciones

- Los ruidos, matemáticamente hablando, son generados mediante secuencias numéricas aleatorias, con una autocorrelación muy baja para todo ...­0, y responden a curvas de densidad de probabilidad del tipo Gaussianas, siendo su comportamiento en el tiempo de tipo estacionario, o sea no presentan variación, estadísticamente hablando, del valor energético involucrado en la misma. Los mismos se pueden clasificar en Blanco, Rosa, Brown (de Browniano) y Negro en función del grado de probabilidad de existencia (entre 0 y 1) que posea cada frecuencia [Hz] 

- La envolvente de la Rxx puede ser interpretada como una medida de cuán bien pueden ser predichos futuros valores de la señal basándose en el conocimiento de valores pasados.

Funciones en el dominio de las frecuencias

La presentación más común de señales individuales complejas (que no son tonos puros) es mediante una descomposición de su magnitud total en las magnitudes de cada componente de frecuencia (llamado comúnmente "espectro").

•Descripción espectral de señales periódicas:

La descomposición en frecuencias está dada por el espectro lineal (de líneas) Px(f). Se aplican directamente los valores discretos resultados de la transformada finita de Fourier definida por:

En las figuras siguientes se observa una señal periódica x(t) y su espectro de líneas Px(f).

  •Descripción espectral de señales aleatorias y estacionarias: 

La descomposición en frecuencias está dada por la función densidad espectral de potencia Gxx(f), también llamada espectro de potencias, función de densidad autoespectral o autoespectro. Se puede demostrar que esta función es la transformada de Fourier de la autocorrelación enunciada anteriormente.

El valor aplicado es la esperanza, valor esperado, E[X(f,T)] o promedio de valores de una muestra infinita de resultados de la transformada de Fourier de bloques de datos estadísticamente independientes.

En las figuras se observa una señal estacionaria aleatoria x(t) y su densidad espectral de potencias Gxx(f).

La integral del espectro de potencia, o sea el área bajo la curva, dadas dos frecuencias límites, f1 y f2, define el valor rms de la señal entre f1 y f2. Si f1=0 Hz y f2=infinitos Hz y µ(x)=0:

•Descripción espectral de señales no estacionarias:

Una señal no estacionaria es aquella cuyas propiedades promedio varían a medida que transcurre el tiempo.

El contenido espectral de este tipo de señales se obtiene mediante la función espectral de potencia instantánea, Gxx(f,t), donde se aplica la transformada de Fourier (anteriormente vista) sobre segmentos temporales cortos, continuos y de duración T. Los resultados se muestran (o deberían mostrar) en tres ejes, amplitud, frecuencias y tiempo. Este tipo de representación se denomina espectrograma.

La integral del espectro de potencia instantáneo en cualquier instante es igual al cuadrado del valor rms de la señal:

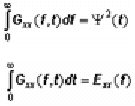Y la integral del espectro de potencia instantáneo a través del tiempo (o sea SE ELIMINA LA VARIABLE TIEMPO), da como resultado la función densidad espectral de energía, Exx.

•Descripción espectral de señales transitorias:

Hay dos funciones utilizadas para describir señales en el dominio de las frecuencias:

• - El espectro de Fourier, el cual es apropiado para transitorios determinísticos (o sea que responden a una función matemática conocida).

• - La función densidad espectral de energía, la cual es apropiada para transitorios aleatorios.

Conceptualmente ambos métodos analizan la señal dentro de una ventana temporal con una supuesta mayor duración que el transitorio. En el caso del transitorio determinístico la ventana es mayor que el mismo, mientras que en el aleatorio se promedian los resultados de transitorios medidos repetitivamente con una ventana T.

Si esta ventana es mayor que la discontinuidad de la señal, ambos métodos arrojan el mismo resultado.

Aplicaciones

- En general se representa sólo la magnitud de la Transformada de Fourier, a pesar que la fase, correspondiente al término imaginario de la misma, posee gran información acerca de la señal. 

- Estos conocimientos son imprescindibles si se pretende realizar mediciones acústicas precisas.

...Todavía no está terminado el tema. No es fácil, pero para aquellos que pretendan un conocimiento formal de la materia es una invitación a la investigación particular en bibliotecas y laboratorios especializados. No queda otro camino. No podíamos continuar hablando de "señales" sin conocer qué es una señal y qué nos puede decir en forma abstracta; o sea ser capaces de entender lo que nos puedan mostrar los instrumentos de medición.