Autor:  Ing. Alejandro Bidondo

En el análisis del comportamiento de sistemas acústicos o de Audio muchas veces es conveniente aplicar las funciones presentadas en las fichas anteriores, las que son para sólo una señal (aleatoria); pero a veces estas funciones no son suficientes o no entregan las respuestas necesarias.

Es ahora el turno de las funciones de unión las que involucran a más de una señal, tanto en el dominio temporal como en el de frecuencias.

FUNCIONES EN EL DOMINIO DEL TIEMPO

•Funciones de Correlación cruzada (Cross-correlation function)

Dadas dos señales aleatorias estacionarias x(t) e y(t) , dentro de un t definido por 0<t<T, cualquier relación lineal entre estas dos será extraída por la función de correlación cruzada Rxy(t).

En el siguiente gráfico podemos observar la correlación cruzada entre dos señales aleatorias de banda ancha o también puede ser de una misma señal captada a dos distancias diferentes de la fuente, siendo t1 el tiempo de propagación entre la primer distancia y la segunda.

Como se puede observar, esta herramienta sirve no sólo para obtener estimaciones de tiempos de retraso sino para analizar cuán decorrelada (o sea, poco correlada, poco relacionada en forma lineal matemáticamente hablando) está una función con otra y para valorar cuán estacionaria es una señal en función del tiempo a efectos de evaluar su estructura temporal y así aplicar luego alguno de los nuevos modelos de la percepción auditiva subjetiva en función de un recinto dado.

•Funciones de coeficiente de Correlación

Para algunas aplicaciones es más conveniente estimar la función coeficiente de correlación dado que se obtiene sólo un número entre cero y uno (r2xy(t)) indicando cuán relacionadas linealmente están las funciones dado un intervalo de tiempo t.

Por ejemplo: si r2xy(t)=0, no existe una relación lineal entre x e y, y si r2xy(t)=1 existe una relación lineal total entre ambas, al intervalo t.

•Funciones de Respuesta al impulso unitaria (hxy(t))

La respuesta al impulso de un sistema físico es aquella salida dada una entrada de tipo "delta de Dirac" normalizada o impulso unitario d(t).

Por lo tanto: hxy(t)= y(t) cuando x(t)=d(t)

La respuesta al impulso (con magnitud y fase) de un sistema L.T.I. (Lineal e Invariante en el Tiempo) caracteriza al mismo completamente.

ðPara los que quieran profundizar:

Dado que el operador neutro para la convolución en el dominio del tiempo es el d(t), al excitar un sistema con dicha señal la salida es la respuesta temporal del sistema. Como este último es invariante en el tiempo, la misma se cumplirá para toda excitación en la entrada hasta t=infinito.

La convolución en el dominio del tiempo discreto se define como:

...por otro lado, la transformada de Fourier de la respuesta al impulso de un sistema es la función Respuesta en Frecuencia.

Creo conveniente aclarar que esta respuesta al impulso (dominio temporal) no siempre es necesario hallarla excitando un sistema con un impulso -de hecho es poco posible generarlo en el mundo real- ; se puede iniciar el análisis desde el dominio de las frecuencias (hallando Hxy(f)) y luego llegar al dominio del tiempo a través de la FFT^-1 (transformada inversa de Fourier).

FUNCIONES EN EL DOMINIO DE LAS FRECUENCIAS

•Funciones de densidad de Espectros cruzados (Crossspectral density functions)

Esta función, también llamada "de espectros cruzados" (cross-spectrum), dará por resultado la relación lineal entre dos señales aleatorias y estacionarias dentro de un intervalo de tiempo T, para diferenctes frecuencias:

, para f>0Hz.

Donde G_xy(f)=C_xy(f)-jQ_xy(f) es un número complejo (magnitud y fase).

Como se puede apreciar el espectro cruzado es la transformada de Fourier de la función correlación cruzada.

Las magnitudes en las ordenadas de esta función serán el  producto de las magnitudes de x(t) e y(t) respectivamente, o sea que las unidades resultarán, por ejemplo: pascales², volts², etc.

•Conclusión: esta función puede ser interpretada como la dependencia lineal de dos señales en función de las frecuencias.

•Funciones de Coherencia (Coherence functions)

Es conveniente normalizar la magnitud de la función de espectros cruzados obteniendo así la función Coherencia, g²xy(f). Esto significa que la magnitud resultante variará desde 0(independencia lineal) hasta 1 (dependencia lineal total), adimensional, siempre en función de las frecuencias.

Donde G_xy(f) es el espectro cruzado definido anteriormente y G_xx y G_yy son los espectros de potencia de x(t) e y(t) respectivamente (transformadas de Fourier de sus respectivas autocorrelaciones -o sea cruzadas "consigo mismas"-).

•Funciones de Respuesta en Frecuencia (Frequency Response functions)

Dadas dos señales x(t) e y(t) que representan la entrada y la salida de un sistema respectivamente, por medio de la función de espectros cruzados, se obtiene la Respuesta en Frecuencia o Transferencia de un sistema, Hxy(f).

Dado que G_xy(f) es una cantidad compleja, H_xy(f) puede ser escrita de la siguiente forma:

Aquí se demuestra nuevamente que la fase posee información válida.

Si este sistema es LTI, su antitransformada de Fourier será la respuesta al impulso antes definida:

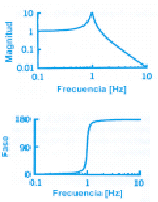
En el siguiente gráfico se observa un ejemplo de respuesta en frecuencia de un filtro donde la magnitud de las ordenadas de la parte real (ganancia) será la de y(f)/x(f) y la de la imaginaria (fase) serán grados.

Varias de estas funciones se encuentran en el instrumental para sistemas de Audio o Acústica e involucran algoritmos de FFT (Fast Fourier Transforms), que son una implementación eficiente de la DFT (Discrete Fourier Transform). El uso eficiente de estas herramientas implica todo lo visto anteriormente más los conceptos de frecuencia máxima, para evitar el aliasing y obtener más resolución en cierta banda de frecuencias, resolución temporal, ventanas temporales y promediación de bloques lo que permite cierta estabilidad estadística en los resultados.

Nuevamente, lo aquí expuesto son conceptos muy complejos pero con la finalidad de que esto sirva como invitación a profundizar en los contenidos de esta disciplina hasta comprender lo anterior (y luego aplicar lo aprendido en investigación, trabajo personal, diseño, educación, etc.).

Mucha suerte y hasta la próxima!