Question:
Problem 6.43: A recent U.S. Bureau of Labor Statistics survey showed that one in five people 16 years of age or older volunteers some of his or her time. If this figure holds for the entire population and if a random sample of 150 people 16 years of age or older is taken, what is the probability that more than 50 of those sampled do volunteer work?

Given:
p = 0.2 = probability that people 16 yrs of age and older volunteers some of his/her time
n = 150 people 16 yrs of age and older

Question 1:

If this figure holds for the entire population and if a random sample of 150 people 16 years of age or older is taken, what is the probability that more than 50 of those sampled do volunteer work?
Find: P(X>50\p=0.2 and n=150)

Solution / Formula 1:
Since p=0.2, therefore the number of people 16 yrs of age and older in a sample size of 150 people is 30 people. It is not therefore possible to find more than 50 people, 16 yrs of age and older to do volunteer work in a population of 150 people. Answer: 0 Population or sample size should at least be n>250 to have a possibility of getting 50 or more people to do volunteer work.

p = .20 or 20% ( 1/5 - volunteer their time)
n = 150 (sample size)

150 x .20 = 30 (30 people only volunteer their time out of 150)
* There is a 0% probability of more than 50 volunteering if the sample size is only 150.

It has to be 250 or more.
Solution: .20(x) = 50
50 /.20 = 250 (sample size should at least be 250)

Answer:

0.00 or 00.00%

Back to: Assignments Main Page

Solution / Formula 2:
Given:
p = 0.2 probability that people 16 yrs of age and older volunteers some of his/her time
n = 150 people 16 yrs of age and older


Solve the following binomial distribution problem by using the normal distribution
P(X>50 \ n =150 and p= 0.2) = ?
Calculating mean and std. Deviation will give
u =n x p = (150) (0.2) = 30.0
St. deviation= sq. rt. n x p x q = sq. rt. (150) (0.2) (0.8) = 4.89

Testing to determine the closeness of the approximation yields
u + 3 st. deviation = 30 + 3 (4.89) = 30 + 14.67
The range of 15.33 to 44.67 is between 0 and 150. Therefore, the problem satisfies the conditions of the test.


Next, correct for continuity : x >49.5 as a normal distribution problem.
Solving for the answer will give Z = (49.5 -30) / 4.89 = 3.987

Based on the Standardized Normal Distribution Table, the probability is 0.49997. Solving for the tail of the distribution yields 0.5000 - 0.49997 = 0.00003

Answer:

0.00003 or 00.00%

Back to: Assignments Main Page

Solution / Formula 3:
Given: n = 150, sample size
p = 1/5 = .2, probability of sample size X > 50

Solution: m = n . p
m = (150) (.2)
m = 30

q = 1 - p
q = 1 - .2
q = .8

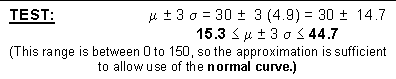
P (X > 50/ m = 30 and s = 4.9) = ?


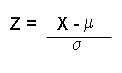
z = (50-30) / 4.9
z = 4.08

* Half of the distribution contains = .5000 of the area. The probability associated with Z = 4.08 is .49997 Subtracting gives the solution:

.5000 - .49997 =. 00003 or .0000

Graphical solutions:


m=30, s=4.9, x=50


z= 0, z= 4.08

Answer:

0.00003 or 00.00%

Back to: Assignments Main Page