|
Question:
Problem 12.17: The equation of a regression
line is: 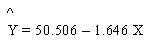
and the data are as follows:
| x |
5 |
7 |
11 |
12 |
19 |
25 |
| y |
47 |
38 |
32 |
24 |
22 |
10 |
|
Solve for the residuals and graph
a residual plot. Do these data seem to violate any of the assumptions
of regression?
Substituting the values of x into the regression
line will give us the predicted value of Y.
Residuals can be computed by deducting
the predicted value of Y from the historical value of Y.
| X |
Y |
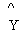
(predicted value of Y) |
Y - 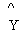 (residuals) (residuals) |
| 5 |
47 |
42.276 |
4.724 |
| 7 |
38 |
38.984 |
-
.984 |
| 11 |
32 |
32.4 |
-
.4 |
| 12 |
24 |
30.754 |
-
6.754 |
| 19 |
22 |
19.232 |
2.768 |
| 25 |
10 |
9.356 |
.644 |
|
The following are the assumptions of simple regression analysis:
1. The model is linear
2. The error terms have constant variances
3. The error terms are independent
4. The error terms are normally distributed
Answer:
Based on the residual plot, we make the following observations.
- It seems that a nonlinear relationship exists between x
and y.
- Also, since a straight line cannot be drawn between the residual
points, the residuals are not normally distributed.
- There appears to be a definite rising and fallling pattern among
the residuals, which strongly suggests a violation of the regression
assumption of independence of error terms.
- The graph seems to indicate non constant error variances.
|





