|
Step 1:
Hypothesis is that the average age of a first-time bride is less
than 24.5 years, but since this is an unproven theory, it is the
alternate hypothesis. The null hypothesis is that the mean is still
24.5 years
Ho : 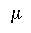 =24.5 =24.5
Ha : 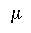 <24.5 <24.5
Step 2: The statistical test to be used is
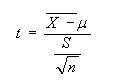
Step 3: The value of alpha is 0.10
Step 4: With 19 data points, df = (n-1) = 19 - 1 = 18. The test
is one-tailed, and the critical table t-value is:
t0.10,18 =- 1.33
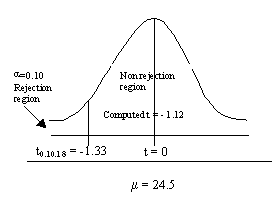
Step 5: Consider sample data above
Step 6:
23.26316 = sample mean
4.817123 = sample standard deviation
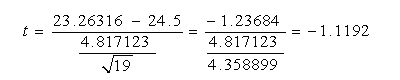
t = -1.12
Answer:
Step 7: Computed
t value of -1.12 is greater than table t value of -1.33, therefore
we fail to reject null hypothesis. Value is within non rejection
area. Average age of first time brides is indeed 24.5.
Back to: Assignments
Main Page
|





