|
Question:
Problem 10.11: Suppose a market analyst wants
to determine the difference in the average price of a gallon of
whole milk in Seattle and Atlanta. To do so, he takes a telephone
survey of 31 randomly selected consumers in Seattle. He first asks
whether they have purchased a gallon of milk during the past 2 weeks.
If they say no, he continues to select customers until he selects
n = 31 people who says yes. If they say yes, he asks them how much
they paid for the milk. The analyst undertakes a similar survey
in Atlanta with 31 respondents. Using the resulting sample information
that follows, compute a 99% confidence interval to estimate the
difference in the mean price of a gallon of milk between the two
cities.
Given: Prices of Gallon of Milk:
| SEATTLE
|
ATLANTA |
| $2.55 |
$
2.25 |
| 2.67 |
2.30 |
| 2.50 |
2.19 |
| 2.61 |
2.41 |
| 3.10 |
2.39 |
| 2.86 |
2.26 |
| 2.50 |
2.19 |
| 2.47 |
2.42 |
| 2.76 |
2.60 |
| 2.65 |
2.38 |
| 2.36 |
2.40 |
| 2.54 |
2.33 |
| 2.54 |
2.29 |
| 2.80 |
2.18 |
| 2.61 |
2.59 |
| 2.56 |
2.38 |
| 2.64 |
2.25 |
| 2.72 |
2.61 |
| 2.73 |
2.25 |
| 2.83 |
2.29 |
| 2.43 |
2.39 |
| 2.43 |
2.40 |
| 2.38 |
2.23 |
| 2.49 |
2.29 |
| 2.57 |
2.53 |
| 2.71 |
2.19 |
| 2.97 |
2.45 |
| 2.65 |
2.33 |
| 2.80 |
2.51 |
| 2.69 |
2.36 |
| 2.71 |
2.44 |
|
|
|
Solution 1:
| SEATTLE |
ATLANTA |
| n1
= 31 |
n2
= 31 |
 1=
2.64 1=
2.64 |
 2=
2.36 2=
2.36 |
| S1
= .17 |
S
2= .12 |
99% confidence interval =  =
.01 =
.01
 / 2 = .005
/ 2 = .005
.50 - .005 = .495
Table A.5 z value = 2.58

Based on this information the confidence interval is :
Formula:

.28 - .096423481 < =  <
= .28 + .096423481 <
= .28 + .096423481
Prob [ .18 <=  <=
.38] = .99 <=
.38] = .99
Answer:
We
are 99% confident that the actual difference in the average price
of a gallon of whole milk in Seattle and Atlanta is between .18
cents and .38 cents. The point estimate is .28.
|
|
Solution 2:
Step 1: The market analyst wants to determine the difference in
the average price of a galloon of whole milk in Seattle and Atlanta,
so this is two-tailed test. The null hypothesis would be:
Ho : =
0 =
0
Ha:  <>
0 <>
0
Step 2: The test statistic is:

Step 3: The value of alpha is .005
99% confidence interval: 1-.99 = .01
.01/2 = .005
Step
4: Z.005 value is ± 2.57
Critical value of Z: .5000 - .005 = .495 = 2.57
The null hypothesis will be rejected if the observed calculated Z
value is less than -2.57 or greater than +2.57.
Step
5: The sample data follows:
| SEATTLE |
ATLANTA |
| n1
= 31 |
n2
= 31 |
 1=
2.64 1=
2.64 |
 2=
2.36 2=
2.36 |
| S1
= .17 |
S
2= .12 |
Step
6: Solving for Z gives:
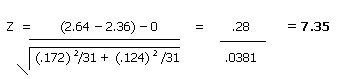
Step
7: Because the calculated value of Z = 7.35 is greater than the critical
table value of Z = 2.57,
the decision is to reject the null hypothesis.
There is a significant difference between the average price of a galloon
of whole milk in Seattle and Atlanta.
Step 8: The evidence shows that between
two cities, on average, Seattle significantly has a higher price
of a galloon of milk than Atlanta. In considering the price market
of new product in these two cities, the analyst should set price
affordable or lower to Atlanta than to Seattle. The diagram displays
the critical Z values, the rejection regions, the calculated Z value,
and the difference of sample means.

The Zc value associated with 99% level of confidence interval is
2.57. Using this value and the other sample information given above,
the confidence interval is:

(2.64 - 2.36) ± 2.57 (.0381)
.28 ± .0979
.18 <= <=.38 <=.38
The analyst is 99% confident that the difference
in the mean price of a galloon of milk between two cities is
$.18 and $.38. The point estimate for the difference in population
mean is $.28.
Back to: Assignments
Main Page
|





