|
Question:
Problem 12.67: Can the consumption of water
in a city be predicted by temperature? The following data represent
a sample of a day's water consumption and the high temperature for
that day.
| |
WATER
USE
(MILLION
GALLON)
(Y - dependent)
|
TEMPERATURE
(X - independent) |
XY |
x2 |
| |
219 |
103 |
22557 |
10609 |
| |
56 |
39 |
2184 |
1521 |
| |
107 |
77 |
8239 |
5929 |
| |
129 |
78 |
10062 |
6084 |
| |
68 |
50 |
3400 |
2500 |
| |
184 |
96 |
17664 |
9216 |
| |
150 |
90 |
13500 |
8100 |
| |
112 |
75 |
8400 |
5625 |
 |
1025 |
608 |
86006 |
49584 |
|
Develop a least squares regression line
to predict the amount of water used in a day in a city by the high
temperature for that day. What would the predicted water usage be
for a temperature of 100 degrees? Evaluate the regression model
by calculating Se, by calculating r2, and by testing the slope.
Let alpha equal .01.
a. Solve for the regression line:
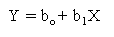
b1 = 
(slope of the regresion line)
b0 =  (Y
Intercept of the regression line)
X
= 608
Y
= 1025
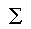XY
=
86006
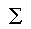x2
= 49584
Regression line: Y = -54.35604 + 2.40107
X
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
b. Solve for the water consumption with a temperature of 100 degrees.
Given the regression equation: Y = -54.35604 + 2.40107
X
Substituting 100 to the variable x will yield a water consumption
of: Y = -54.35604 + 2.40107 (100)
Water consumption = 185.751 million gallons
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
c. Solve for Se (Standard Error of the Estimate):
| |
x |
y |
y2 |
xy |
x2 |
| |
103 |
219 |
47961 |
22557 |
10609 |
| |
39 |
56 |
3136 |
2184 |
1521 |
| |
77 |
107 |
11449 |
8239 |
5929 |
| |
78 |
129 |
16641 |
10062 |
6084 |
| |
50 |
68 |
4624 |
3400 |
2500 |
| |
96 |
184 |
33856 |
17664 |
9216 |
| |
90 |
150 |
22500 |
13500 |
8100 |
| |
75 |
112 |
12544 |
8400 |
5625 |
|
608 |
1025 |
152711 |
86006 |
49584 |
|
Compute for SSE (Sum of squares Error) first.
SSE formula: 
b0 =-54.35604
b1 = 2.40107
SSE = 152711 - (-54.35604)(1025) - 2.40107(86006)
SSE = 152711 + 55714.941 - 206506.4264
SSE = 1919.5146
Then compute for Se (Standard Error of the Estimate)
Se formula:
Se = sqrt. of (1919.5146 / 6)
Se = 17.886
Interpretation:
Standard
Error of the Estimate (Se): 17.886
17.886 is the standard deviation of the error.
If the error terms are normally distributed, the empirical rule
states that given the values of X, approximately 68% of the error
terms would be within + - 17.886 and 95% would be within + - 2(17.886).
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
d. Solve for r2 or coefficient of determination:
proportion of variability of the dependent variable accounted for
or explained by the independent variable.
r2
formula: 
SSyy = 1 - SSE
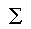/ y2
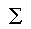- (Y)2
/ n
SSyy = 21382.875
r2 = 1 - (1919.5146 / (21382.875)
)
r2 = 1 - .089768779
r2 = .91023122 or
.91
Interpretation:
Coefficient
of determination
r2 = .91
The coefficient of determination is the proportion of variability
of the dependent variable (Y) accounted for or explained by the
independent variable (X). The coefficient of determination ranges
from 0 to 1. A r2 of .91 or 91% means that 91% of the variability
of Y is accounted for or predicted by X. It also means that 9% is
not explained by the regression model.
91% of water consumption is determined by
the temperature.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
e. Test the slope of the regression line
with alpha of .01
Y model :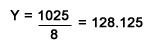 
Test if slope is equal to zero.
H0 : b1
= 0
Ha : b1
<> 0
This is a two-tailed test:
= .01 /
2 = .005
df = 8-2 = 6
t
value from table A.6 = 3.707
Solve for computed value of t:
t
formula: 
SSxx
= 
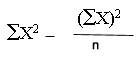
SSxx
=
3376
Se
= 17.886
Sb = 
Sb = .307830755
t = 2.40107 - 0 / .307830755
t = 7.799967875 or 7.80
Graph:
Interpretation:
We reject the null hypothesis. 7.80 lies in the rejection region.
The slope is not equal to 0. The regression model adds more predicative
information than the Y model of no regression or simply getting
the average of Y.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
Fit
of the line:
The regression model rejected the null hypothesis
because 7.80 lies in the rejection region. The model therefore is
a good a fit.
Also it has a high r2 or coefficient of determination of 91%.
|
