Question:
Problem 2a: Significance of Coefficient
Test the slope of the regression line with alpha of .01

Y model :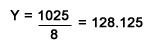
Test if slope is equal to zero.
H0 : b1 = 0
Ha : b1 <> 0

This is a two-tailed test:
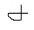= .01 / 2 = .005
df = 8-2 = 6

t value from table A.6 = 3.707

Solve for computed value of t:

t formula:
SSxx =
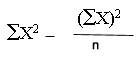
SSxx = 3376
Se = 17.886
Sb =

Sb = .307830755

t = 2.40107 - 0 / .307830755
t = 7.799967875 or 7.80

Graph:

Interpretation:
We reject the null hypothesis. 7.80 lies in the rejection region. The slope is not equal to 0. The regression model adds more predicative information than the Y model of no regression or simply getting the average of Y.

Problem 2b: Significance of Correlation
Step 1:
This is a two -tailed test with the following hypothesis:
Ho: p = 0
Ha: p not equal to 0

Step 2:
The test statistic is:

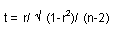
Step 3:
The alpha is .01, since it is two tailed, divide it by 2 will give you: .005

Step 4:
The degrees of freedom is: n-2 = 8-2 = 6 with alpha =. 005
The critical t value is: t.005, 6 = ± 3.707

Step 5:
The following are computed from the given data ( problem 12.67)


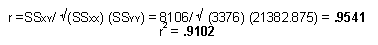
Step 6:
The calculated t value is:

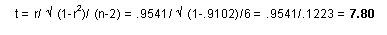
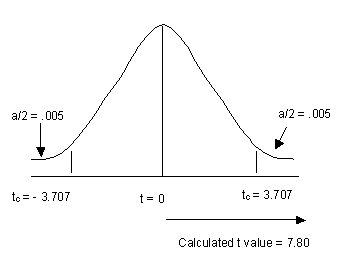
Step 7:
Since the calculated t value 7.8 is in the rejection region, we reject the null hypothesis. This is shown in the following graph:


This sample provides sufficient evidence to conclude that a positive correlation exists between the temperature and water used in a day.

EXCEL SOLUTION

The r value obtained represents a relatively strong positive relationship between temperature and water usage in a day. 95% of water consumption is determined by the temperature.