Question:
Problem 11.13: A management consulting company presents a 3 - day seminar on project management to various clients. The seminar is basically the same each time it is given. However, sometimes it is presented to high-level managers, sometimes to midlevel managers, and sometimes to low-level managers. The seminar facilitators believe evaluations of the seminar may vary with the audience. Suppose the following data are some randomly selected evaluation scores from different levels of managers after they attended the seminar. The ratings are on a scale from 1 to 10, with 10 being the highest. Use a one-way ANOVA to determine whether there is a significant difference in the evaluations according to manager level. Assume alpha = .05.

Given:

HIGH LEVEL MIDLEVEL LOW LEVEL     7 8 5     7 9 6     8 8 5     7 10 7     9 9 4     10 8       8   TOTAL(rows): 38 62 35 135 n 5 7 6 N =18 7.6 8.86 5.83 7.5

Manual Solutions:

ANOVA - Analysis of Variance

Step 1: The hypotheses are:

Ho:
Ha: At least one of the means is different from the others

Step 2:
The appropriate test statistic is the F test calculated from ANOVA.

Step 3:
The value of alpha is .05.

Step 4:
The degrees of freedom for this problem are:
dfc = C -1
dfc = 3 -1 = 2

dfe = N - C
dfe = 18 -3 = 15

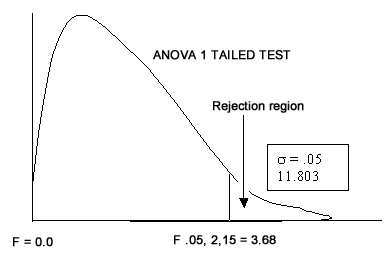
F table A.7 value = F.05,2,15 = 3.68

The critical F value is 3.68. Because ANOVAs are always one-tailed with the rejection
region in the upper tail, the decision rule is to reject the null hypothesis if the
observed value of F is greater than 3.68.

Step 5:

	HIGH LEVEL	MIDLEVEL	LOW LEVEL
	7	8	5
	7	9	6
	8	8	5
	7	10	7
	9	9	4
		10	8
		8		TOTAL(rows):
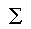	38	62	35	135
n	5	7	6	N =18
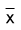	7.6	8.86	5.83	7.5

Step 6:
Partition the total variance of the data into 2 variances:
a. Variance resulting from the treatment
b. Error variance, portion of the total variance unexplained by the treatment.

SST = SSC + SSE
(total sum of squares) = (treatment sum of squares) + (error sum of squares)

SSC =

SSC =

SSC = 29.7306
---------------------------------------------------------------------------

SSE =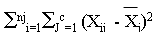

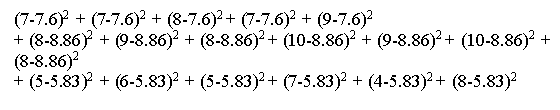
SSE = 18.8906
---------------------------------------------------------------------------

SST =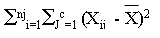

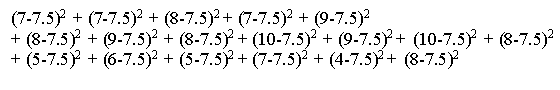
SST = 48.5
---------------------------------------------------------------------------

MSC = SSC / dfc

MSC = 29.7306 / 2

MSC = 14.8653

MSE = SSE / dfe

MSE = 18.8906 / 15

MSE = 1.259373333
Computed F = MSC / MSE

F = 14.8653 / 1.259373333

Computed F = 11.80372778

F table A.7 critical value = F.05,2,15 = 3.68


Step 7:
The decision is to reject the null hypothesis because the observed F value of 11.80 is greater
than the critical F table value of 3.68.


GRAPH:

Step 8:

Computed f value of 11.80 is greater than table f value of 3.68, therefore we reject the null hypothesis. Not all means are equal. There is a significant difference in the evaluations depending on the manager levels.

--------------------------------------------------------------------------------------------------------------------

Click below for:

EXCEL SOLUTION

Back to:Finals Main Page