Question:
Problem 7.22: According to Medirisk, Inc. people's perceptions of the costs of health care are not always even close to the actual costs. For example, the average actual cost of medical care for a broken arm is $418. A U.S. survey by Medirisk found that the average estimate by Americans for the cost of a broken arm was $583, with a low estimate of $10 and a high estimate estimate of $3,800. Suppose you took a survey of 42 people who had experienced a broken arm and received medical care for it during the last year and ascertained the actual cost of medical care in each case. Suppose the actual average medical cost for a broken arm in the United States was $418 with a standard deviation of $85.

a. What is the probability that the sample average will be more than $430?
b. What is the probability that the sample average will be less than $400?
c. What is the probability that the sample average will be less than $350? Suppose your sample average actually is less than $350. What could this mean?
d. Suppose the population standard deviation is unknown. If 71% of all sample means are greater than $410 and the population mean is still $418, what is the value of the population standard deviation?

A.:
What is the probability that the sample average will be more than $430?

Solution / Formula:
m = $ 418 actual average medical cost for a broken arm
s = $ 85
$ 583 - average cost for a broken arm low of $ 10 and high of $ 3,800.
42 - sample size



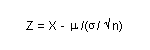
z = (430 - 418) / (85 / sqrt. of 42)

z = 0.9149 or 0.91

Using the table: P = 0.3186



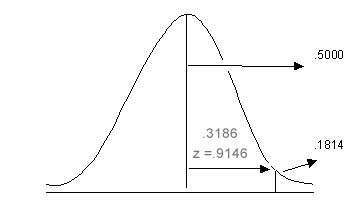
.5000 - 0.3186 = .1814 or 18.14%

Answer:

P (X>430) = 0.1814 or 18.14%

B:
What is the probability that the sample average will be less than $400?

Solution / Formula:
m = $ 418 actual average medical cost for a broken arm
s = $ 85
$ 583 - average cost for a broken arm low of $ 10 and high of $ 3,800.
42 - sample size



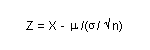
z = (400 - 418) / (85 / sqrt. of 42)

z = - 1.3724 or - 1.37

Using the table: P = .4147



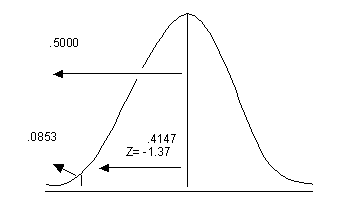
.5000 - 0.4147 = .0853 or 8.53%

Answer:

P (X<400) = 0.0853 or 8.53%

C:
What is the probability that the sample average will be less than $350?
Suppose your sample average actually is less than $350. What could this mean?

Solution / Formula:
m = $ 418 actual average medical cost for a broken arm
s = $ 85
$ 583 - average cost for a broken arm low of $ 10 and high of $ 3,800.
42 - sample size



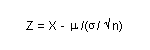
z = (350 - 418) / (85 / sqrt. of 42)

z = - 5.18456 or - 5.18

Outside the area of the standard normal distribution.

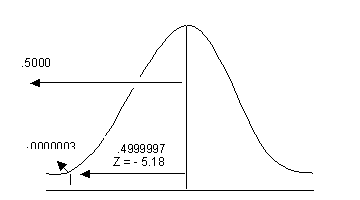
Answer:

P (X=0) = 0.00 or 0.00%

D:
Suppose the population standard deviation is unknown. If 71% of all sample means are greater than $410 and the population mean is still $418, what is the value of the population standard deviation?

Solution / Formula:
m = $ 418 actual average medical cost for a broken arm
42 - sample size

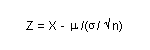
Probability = (.71 - .50 = .21)

Using z table, z = 0.55






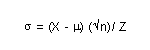
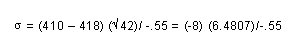
s = $ 94.26 or 94

Answer:

$ 94.26

Back to: Mid Term Main Page