Although very useful, pulses create their own problems. Caused by rapidly changing current rates through the motor, the most obvious are increased heat, followed by driver tread wear; polished, slippery rails and reduced traction; through the hidden wear in bearings and gears to eventually noise. Pulses must be used judiciously with knowledge.
An electrical pulse is any deviation from a straight line, constant voltage, current or power level. They may be unipolar, limited to one side only, or more often, bipolar on both sides. All pulses are not created equally and some are more equal than others. Measurements have been standardized, but variations in interpretation exist. In practice, the theoretical values of parameters are never reached. They may be periodic, coded, intermittent or random as with noise. For the theorist, all pulses can be broken down to a harmonic, sinusoidal series by Fourier analysis and the faster the transition times and the sharper the corners, the higher the harmonic frequencies and amplitudes. Only the simpler properties relevant to modelrailroad usage will be discussed here.
Since every circuit generates them, the most common and least desirable are random noise. From vibrating molecules to arcing motor brushes, everything contributes it share. Sizes, shapes and times usually vary drastically, but rarely, some may repeat themselves regularly. By superimposing themselves on signals, they may be large enough to render a circuit useless. Short time, high amplitude spikes are usually the most dangerous, since they may punch through insulation or generate enough heat to burn out components. Lightening is an extreme, but good example. The quality of a circuit is judged by its signal to noise ratio. Well designed circuits have components that reduce noise to a tolerable level.
Probably the most common useful types are periodic or repeating at regular intervals. A very large percentage of these are sinusoidal or sine waves as in line voltage, radio and TV carriers and single tone sound. They may be continuous or come in bursts. Computer and other clock circuits produce a variation of these that are rectangular in shape. While TV and monitor sweep circuits use saw tooth variations. Many intelligence or control circuits have periodic index pulses with variable information pulses between. These include modems, radio control and even DCC.
Quasi random or intermittent pulses occur everywhere and from extremely short as in computers and radar, medium in keyboards and push buttons; and extremely long in light or power switches. They may be sequential in control circuits or many computer instructions and functions. Often they are synchronized with clock pulses.
The important measurements are amplitude, rise and fall time, width and period (rate or frequency). For critical circuits, there are many others of little value here. An oscilloscope is required to view and measure them. Only a well compensated high frequency band width scope can display some of the finer parameters. Since in many practical circuits, pulses have spike like, over shoot at the ends of transition, determining some of the parameters may prove difficult.
Amplitude is usually measured as peak, from reference level to maximum value; peak to peak, from minimum to maximum pulse values; but in some cases effective DC equivalents are used for sine waves and other forms in power circuits. The commonly used RMS (root-mean-squared) value of sinusoidal pulses is approximately .707 the peak measured from ground reference. This is used for AC line voltages and currents as well as rectified waves in power supplies.
Since circuit capacitance and inductance curve them in opposite directions, absolutely straight lines can not be produced by present circuits. All pulses are curved and all corners are rounded to some degree. Of very little consequence in this discussion, these will be ignored here for simplicity .
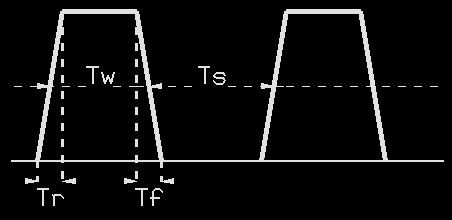
At the leading edge, the time it takes to reach the peak is the rise time (Tr) and at the trailing edge the time to go back to zero is the fall time (Tf). In practical cases the exact start and end locations are sometimes quite difficult to determine. Some cases require very short values to reduce time variations, since either may be used to trigger or synchronize other circuits. For power packs, values are only critical to jog armatures and reduce heat and other undesirables.
Note: Adjust brightness and contrast for optimum viewing.
Simplified pulse measurements.
Usually measured at the half amplitude points; width, spacing and period are all interrelated. In most cases pulse width (Tw) is taken as the signal-on time, but as in the so called "digital" model airplane RC set, the pulse is carrier off. Since the carrier is on, except for pulse time, the possibility of noise reception is reduced. The spacing (Ts) is the time from the trailing edge of the first pulse to leading edged of the next pulse. The sum of the two is the period:
(Tp = Tw + Ts). For periodic pulses or those that recur with a fixed period, the reciprocal of the period is the pulse rate in pulses per time in the same dimension; or in seconds, the frequency in cycles per second (Hertz). F sec= 1/Tp sec. Thus the common 60 Hertz line frequency has a period of .016667 sec = 16.667 ms. For periodic pulses Tp may be measured between any two respective points on any two adjacent pulses.
In purely resistive circuits, Tr and Tf have no effect on components. While in semiconductors, effects vary. In simple junction devices, heat is generated during the change, but very little is developed at the off and saturation (full on) points. To increase light output, LED's are often pulsed with higher than rated currents, using a duty cycle which yields the equivalent of the effective rated value.
In capacitive and inductive reaction circuits, these values may be very critical to aid or hinder functions. Reactive circuits are used both to create and destroy pulses. Quite frequently, they reduce the effects of transition times by reducing the amplitude, increasing the time or both, through frequency band filtering.
Of utmost importance in powering motors, are the effects of inductive reaction combined with rapid current change. In a lossless theoretical world there is no problem, all energy applied to a reactor is returned to the circuit in the opposite direction, resulting in zero consumption. But we live in a lossy world, where many leaks occur. First, heat is a molecular vibration, which may include the entire body as a whole, due to external friction. The quantity of heat is an energy measured in calories. In physics. velocities are vectors with not only a magnitude but a direction. Any change in either is considered an acceleration which requires energy. Using a car for analogy, the energy used to accelerate to 60 MPH is greater for less time or higher speed.It is not returned to the gas tank, but eventually is dissipated as heat. The same happens in a motor, but the culprit is not the engine. It is a calculus differential di/dt or the instantaneous rate of change of the current with respect to time. On a larger scale, this is approximated by the amplitude of the current pulse divided by either Tr or Tf.


Note: Adjust brightness and contrast for optimum viewing.
L: Incremental display of Di and Dt, the respective changes between two points on curve.
Ds is the average slope of curve.
R: Differential display of di/dt with slope line ds, tangent to curve.
In the left drawing, Dt is the rise time between the end points and Di is the current change. By moving the points closer together, the triangle shrinks down and Ds moves closer to curve. Accepted on faith by calculus students, the triangle can be shrunken down to zero size, where it becomes a point. The value then is the instantaneous rate of the current with respect to time. The differential drawing shows the relationship just before this happens.
Through changes in speed and direction, this rate of change in the current accelerates the armature magnetic field which in turn accelerates every magnetic dipole molecule in range. Although the bulk of the energy goes into the ferro-magnetic pole pieces and armature, a minute amount goes into the para-magnetic copper molecules to add to the resultant heat. The total result may be great enough to vibrate the whole motor or even the loco.
Of great interest in pulsed power packs is the duty cycle or the ratio of D = Tw/Tp. This yields the effective DC value as a fraction or percentage of the straight line DC value at the peak level. If a 12 V peak pulse is on 1/4 of the period, the effective voltage is 3 V. For odd shaped waves, the ratio of the areas is found by narrow, vertical slicing and adding the slices together. With luck, often in engineering, adding together an infinite number of infinitesimal slices is simulated by calculus integration methods. This is how the RMS value for a sine wave is derived.
The following is extensively simplified to reduce the "snow" factor. In addition only very simple wave forms will be shown, since actual current waves are very distorted by commutator noise and 10 pulses per revolution on a 5 pole motor. At 1000 RPM there are 10000 PPM = 166.67 PPS. Dividing by the 120 HZ power pack pulses, there are about 1.39 motor pulses per pack pulse. The motor would be synchronized at 720 RPM or around 3 to 12 SMPH for common locos. On some locos, this may be noticed as a slight hesitation in acceleration at low end speeds. Since the frequency range of armature pulses overlaps the pack pulse frequency, it is extremely difficult to separate them. This accounts for the lack of success in speedometers dependent on motor RPM.
The most common pulses in power packs are the full wave rectified sine waves, followed by half wave. Except possibly in heavy industrial areas, the 60 HZ power line supplies an almost pure sine wave with minimal harmonics, that might cause problems greatly change pulse shape. When graphing current functions, di/dt represents the slope of the curve at that point. The value can be found from the derivative of the sine which is the cosine. Looking at the cosine function, at zero its value is maximum at 1. Following the sine curve, the cosine and di/dt gradually reduce until at the sine wave peak or 90 °, the value equals zero.
Analysis reveals that for each quarter of the rise time the percentages of the current changes are about 38, 32 22 and 8. It is evident that most of the heat is produced down toward the zero level.
Based on an analogy from Ohms law that power loss in a resistor is P = I^2 * R , in differential equations, power in an inductor takes the form of L * (di/dt)^2. Where L is the inductance in Henry's . This means that power losses are dependent on the square of the rate of change of the current.

Note: Adjust brightness and contrast for optimum viewing.
Full wave rectification plus half wave or pulse power.
Rectification causes every other half cycle to flip polarity, resulting in a pulse rate of 120 pps. Half wave or pulse power removes every second pulse, producing a gap between the remaining 60 PPS. For full wave the effective value is .707 peak, while for half wave it is half that at .3535.

Note: Adjust brightness and contrast for optimum viewing.
Full wave rectification plus half wave or pulse power showing the effect of one piece of reactive filtering..
As a result of the inductance and distributed capacitance of the coils, the spaces between the current peaks tend to fill in. The current lags the voltage by a circuit dependent number of degrees, the cosine of which is often called the power factor. By far the greatest effect is caused by the LR time constant in seconds, which is derived from multiplying the motor inductance L in henries by the resistance in ohms. The effect is an exponential curve with decreasing slope in the rise and fall in opposite directions. By increasing filtering externally, an almost constant DC level, with very low ripple (pulses) can be achieved. Using filtered DC at higher levels and speeds, most motors and locos perform excellently with minimum heating due to only I^2 R losses and friction.
BACK TO POWER PACKS
Often called inductive kick, another phenomenon frequently occurs, if the flux producing current is cut off abruptly. The magnetic field collapses immediately, producing a very large current surge which can burn out resistors. More often it is observed as a large, sharp voltage spike across the resistance, which can arc across switches or punch through semiconductors and capacitors, causing damage. This is very common with switched devices as solenoids in switch machines and relays, requiring high voltage, protective, bypass diodes or capacitors in most circuits. Fortunately the levels are small in model motors, appearing as arcing at the commutator, but still contributing to plate and brush wear.
For full wave, the LR curves smooth the pulses somewhat so they usually do not fall to zero level thus reducing the effective amplitude and slopes. This reduces di/dt almost everywhere, which in turn reduces the potential heat generation. However with most motors using half wave, the pulse can fall to zero, increasing the effective amplitude and slopes. The negative going space pulse resembles a rectangular one. With a duty cycle of 1, full wave effective current approaches 100% of the peak. While half wave has a much lower duty cycle due to the larger gap. Since the conduction speed of heat is close to the speed of sound, there is very little dissipation in the gap time. To produce equivalent running speeds, half wave peak current must be much higher, increasing di/dt even more. This adds up to values that appear to be much more than 2 times greater, producing the very noticeably increase in heat at higher speeds.
BACK TO CAPACITIVE SWITCH MACHINE POWER SUPPLIES
Since transistorized packs were introduced, many types of pulses have been offered, varying in shape, amplitude, duty cycle and rate. Most have been unsuccessful and thus disappeared. Since large values of di/dt are desirable to jog armatures but produce more heat, compromises must be made. The most successful seems to provide high values at starting, stopping and low speed running, while attenuating as speed increases.
Shapes are usually limited to those easiest to produce, such as rectangular, triangular, saw tooth and modified sinusoidal, each with its own advantages and disadvantages.
Useful as a very good yard throttle, one of the easiest is made by replacing the throttle transistor with a silicon controlled rectifier (SCR), which can be switched on at any time throughout the packs sine pulse. The new leading edge is almost vertical producing a good armature jolt with increased heat. Both amplitude and duty cycle are altered, but control is far from linear. The device is switched off only when the current through it reaches zero at the end of the sine pulse, however, some times internally, additional circuitry has been developed for earlier turnoff.
Note: Adjust brightness and contrast for optimum viewing.
SCR trigger points.
With simple level triggering only the leading edge up to peak of sine pulse can be triggered on. By using timed triggering devices almost the entire range can be used. The jolt and most of the heat are determined by the amplitude of the sharp leading edge. Both are greatest for triggering near the peak. This may be considered quasi disappearing pulsing in that very early switching approaches full wave. Overall the heat is less than with half wave. Since the period is fixed by the line frequency, no adjustments can be made.
Excluding the sinusoidal, in most applications, the remaining types are applied to a well filtered, constant level DC.
The rectangular pulse is the easiest to generate using various types of multivibrators as switches. All parameters can be adjusted by selection of fixed or variable components. The fast rise and fall times can provide the greatest jolts, but produce the most heat. The rapid fall time greatly increases inductive kick. Amplitude or duty cycle can have a large bearing on all these values. The worst cases exist with high peak values of full throttle voltage or above, as in pulse width speed control, along with high duty cycle. Not only is di/dt maximized, but dissipation time is minimized, resulting in maximized heat retention. Using high amplitude pulse for short start or stop periods during acceleration, can produce excellent momentum effects. But reducing them toward zero as smoother current level rises can greatly alleviate the heat problem.

Note: Adjust brightness and contrast for optimum viewing.
Through filtering, the remaining common pulses are derived from rectangular ones, by increasing the rise or fall times to form ramps. The saw tooth may have either changed. For the fast leading edge, the properties are the same as rectangular. For the trailing ramp with its constant di/dt, the value is greater than a sinusoidal near the peak, but less near zero and contributes a minor amount to jolt. Flipping horizontally the characteristics are basically the same, except the sharp trailing edge fall greatly increases inductive kick. The triangular pulse has ramps on both leading and trailing edges and is thus the least effective. As the pulse width narrows all these pulses approach rectangular, not only in shape but in characteristics.
Although commonly done in uninterruptible power supplies with battery backup, generating sine waves from steady DC is a design mess. A stepped pulse is developed, with small steps approximating the sine curve to reduce filter requirements . Then low pass filtering is applied to reduce and round the jagged edges by attenuating the harmonics. Usually the result is a not too clean, but acceptable, rippled sine wave.
Choosing pulses or combinations for powering locos, may appear overwhelming, but by elimination and needs, the choices narrow down quickly. Only you can determine the requirements and trade offs that will satisfy your mode of operation and pocket book. Most commercial pack or system information presents hype rather than pulse parameters. Only the positive selling features are stated, while the negatives are conveniently omitted. Unfortunately only, possibly expensive, trial and error may reveal the true facts. Reliable feedback with an understanding of pulse characteristics can help. The question of momentum may have a strong bearing on choice. Although not always included, it can be built into any scheme.
The first to go would be triangular and saw tooth, leaving sinusoidal and rectangular. Ubiquitous sinusoidal packs with full or half wave can be evaluated almost anywhere. SCR packs with their good performance are more scarce. These may be all that you need or want.
Since most of the more expensive and sophisticated schemes, apparrently use rectangular alone or superimposed on momentum ramps, this is where analysis comes in. The pros and cons must be weighed carefully. Large di/dt is useful in jolting sluggish armatures, but there are limits. The only way to control di/dt in rectangular pulses is to vary the amplitude. Too much can spin drivers slightly under heavy loads, resulting in tread wear, polished rails and loss of traction, not to meantion the other negative effects of hidden wear, heat and vibration. Driver spin caused by large di/dt is probably the major cause for tread wear, even at high speeds, where it is likely to go undetected. The only other major contender is the practice of overloading locos to the extent that drivers spin under any type of propulsion. Amplitude should be limited to only the value necessary and pulses applied only when needed.
Changing duty cycle, Tw and Ts can only vary di/dt, if the spaces between pulses fill in by reactance to a point where peak to peak amplitude is reduced. Varying with rate and motor inductance, this can influence the use of pulse width or duty cycle speed control. Insufficient cooling time between pulse transitions usually allows heat build up. With a little analysis it can be seen that the quantity of di/dt heat is independent of the pulse width, if the pulses return to zero. Among direct to the rail packs, this type of throttle has never been too sucessfull. Present DCC systems appear to suffer from these problems.
Since smooth DC produces the least negative qualities with good perfomance at higher speeds and rectangular produces the most negative with the best jolt for lower speeds, a compromise between the two seems to be the best choice. If reasonable rectangular pulses are applied at lower speeds and diminished at higher, as the DC level increases, the best of both can be combined. In addition the undesirable effects, can be reduced. The solution is relatively simple. Through negative feedback of the DC voltage to the pulse generater, the pulse amplitude can be reduced as the DC level rises. This is commonly referred to as a squelch circuit, which works well with momentum ramps.
A major problem with any approach is that inductance of motors varies greatly as do loads and current draw. In the selection of pulse rate or frequency, another problem is that armatures have electrical resonent frequencies, while any part of the loco can have mechanical resosoneces at different frequencies. These may cause unwanted hesitation or noise. Even a carefully chosen system will probably not suit all locos in all parameters. While increasing comlexity, adjustability of some or all may be the only solution.
Mamaging to unstand these basic principles, should provide a foundation for pulse selection. Remember, the choice is yours.
BACK TO POWER PACKS
BACK TO LOCOMOTIVE TESTING
BACK TO SCOPE
