Supongamos que tenemos una e.d.o. lineal homógenea de segundo orden con coeficientes variables:
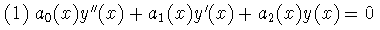
incluso si ai(x) para i=0,1,2 fueran polinomios, encontrar la solución es bastante complicado.
Supongamos que
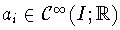con i=0,1,2, x0
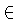I
(I es un intervalo abierto). Vamos a intentar encontrar el
desarrollo en serie de potencias de la solución alrededor
de x0 : 
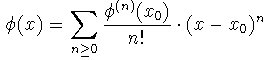
Si conociera
,
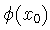, entonces, despejando
en (1) obtendría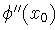 
.
Derivando la ecuación obtendría todos los
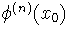. Por tanto, lo que hay que
justificar es la convergencia de la serie. Vamos a resolver la ecuación:
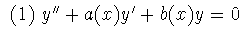
Definición: Sea x0
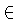
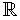. Diremos que
x0 es un punto regular para (1) si
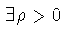tal que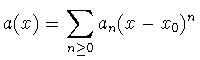 
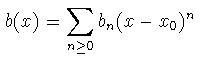
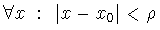
i.e., si a(x), b(x) son analíticas en x0. Si esto no sucede, se dice que x0 es un punto singular. Si x0
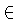
es singular para (1)
y (x-x0 )a(x),
(x-x0 )2 b(x) son analíticas en
x0 entonces diremos que x0 es
singular regular. x0 es un punto regular de (1).
Veamos si podemos determinar una solución de (1) de la forma
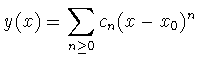
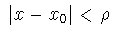
que sea solución de (1)
Derivemos esto y sustituyamos en (1) a ver qué condiciones nos da sobre los coeficientes cn :
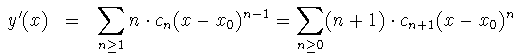
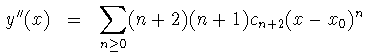
Como a(x), b(x) son analíticas en x0, para multiplicar por y'(x) e y(x) hacemos su producto de Cauchy:
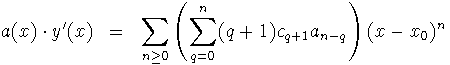
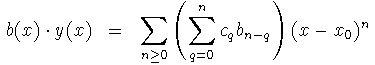
Sustituyendo todo en la ecuación se llega a:
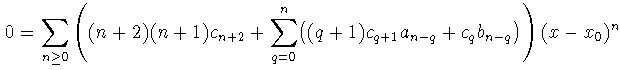
Como la suma ha de ser cero en
,
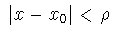los coeficientes deben valer cero, es decir: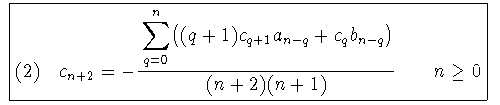 
cn+2 es, en principio, función de c0 , c1 , ..., cn+1. Pero una vez fijados c0 , c1 se obtienen todos los demás términos (c0 , c1 dependerán de las condiciones iniciales). Es decir, cn para n
2 es
función de c0 , c1. TEOREMA: Sea x0 un punto regular de (1). Sean c0 , c1
. Entonces,
existe una única solución de 
en
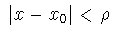dada por la serie de potencias convergente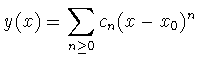
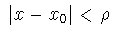
donde cn para n
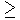2
se obtienen mediante la fórmula de recurrencia (2).
x0 es un punto singular regular de (1).
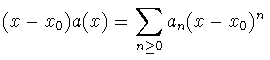
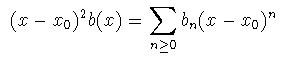
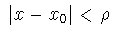
La ecuación original, multiplicada por (x-x0)2 , queda:
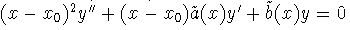
Con
,
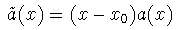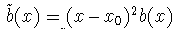analíticas en
x0. Vamos a hacer un abuso de notación y
seguir llamando a estas 
como antes: a(x), b(x). El objetivo ahora es buscar soluciones de la forma:
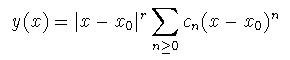
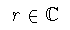
que reciben el nombre de series de Frobenius.
Vamos ahora a realizar todos los cálculos necesarios y después sustituir en (1).
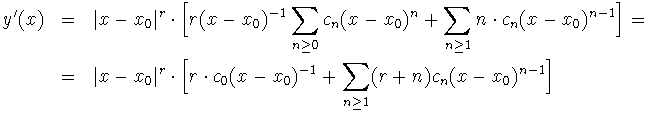
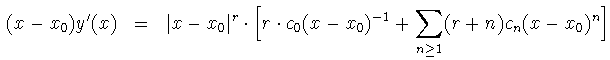
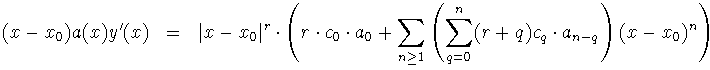
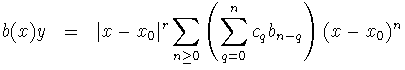
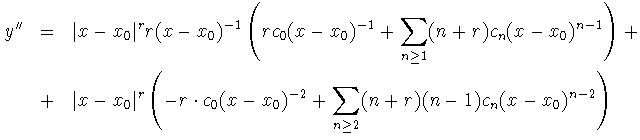
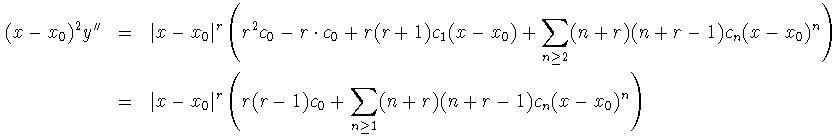
Sustituimos ahora todo en (1) y se tiene:
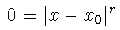
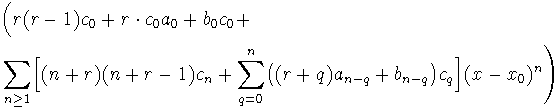
Debe cumplirse, pues:
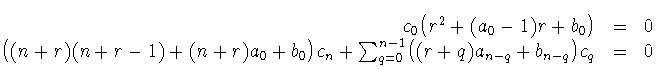
eligiendo c0
0 Introducimos la función F(r)=r2 + r(a0 - 1)+ b0. Si F(r)=0, la llamamos ecuación indicial. Se elige c0
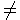0, pues
si c0 = 0, entonces cn =0
n. Luego queda el sistema:
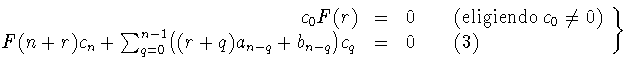
Así que, de entrada, r no puede ser cualquiera, si no que debe ser solución de la ecuación indicial. Veamos los casos posibles.
Raíces complejas:
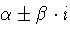con
,
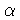
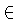
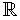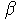
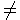0.
En este caso, F(n +
+
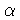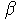i)
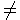0 para
n 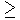1 y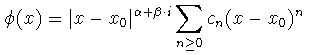 
con c0
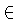
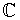-{0},
cn
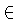
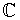para n 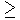1
determinadas por (3) para
r =
+
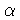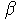i
es una solución de (1). Se cumple además que
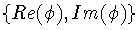es un sistema fundamental (real) de (1). Raíces reales iguales: r2=r1
Para r
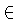[r1 - 1/2,r1 + 1/2] definimos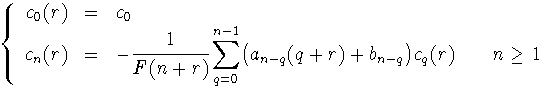 
Entonces
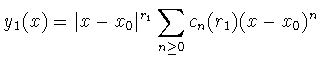
es la solución ya obtenida, y la siguiente es una segunda solución linealmente independiente de y1(x):
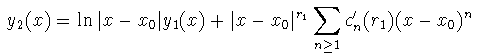
Raíces reales distintas: Si tenemos r1
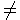r2 , siendo r1 , r2
,
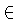
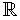tomando por ejemplo r2 > r1 , entonces
F(n + r2 )
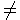0
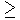para n 1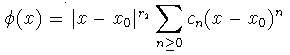 
con c0
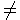0 y
cn para n
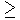1
obtenidos mediante (3) con r=r2 es una
solución de (1). Ahora, aquí podemos tener dos subcasos.
1. Diferencia de raíces no natural: Si r2 - r1
,
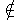
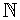entonces F(n + r1 )
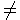0 para
n 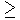1.
Si tomamos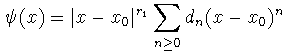 
con d0
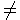0
y el resto de los dn mediante la fórmula
recurrente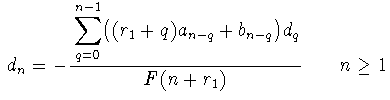 
se tiene que es una solución de (1) linealmente independiente de
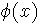
2. Diferencia de raíces natural: Si r2 - r1
,
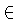
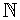eso significa que
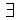n0
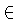
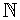tal que r2 - r1 = n0 Vamos a tomar los coeficientes cn (r) como en el caso en que las raíces reales eran iguales, pero tomando un valor distinto para el c0 (r) y el cn0 (r) (es el término problemático). La elección de los coeficientes es, pues:
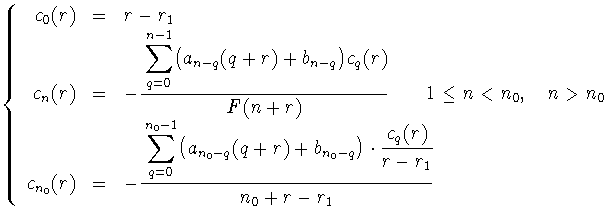
La segunda solución linealmente independiente es:
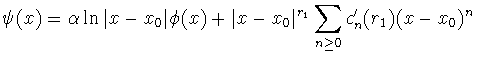
siendo
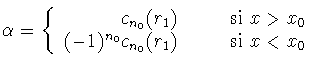
De vuelta a GeoCities