El objetivo de este pequeño texto es encontrar expresiones para la integral definida entre 0 y x de la función
pues, como sabemos, esta función no tiene primitiva expresable
como combinación finita de funciones elementales. Para calcular
la integral de esta función sobre toda la recta real se requieren
técnicas de variable compleja; este punto no lo vemos aquí.
El por qué es sencillo: para la integrale definida que
calcularemos, los límites de integración son
números reales, puesto que se verá que la convergencia
de la serie de potencias resultante del desarrollo de la función
dada es uniforme en los compactos de
,
lo que obliga a buscar otros métodos cuando el intervalo es de
longitud infinita. Veamos pues si podemos encontrar algún desarrollo para la integral definida de la función
al menos en algún intervalo compacto de la recta. En primer lugar hay que calcular el desarrollo en serie de potencias de esta función. Sabemos que
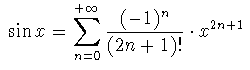
Dividiendo por x, tenemos que:
Lo primero que tenemos que averiguar es cuál es el radio de convergencia de dicha serie (pues eso nos dirá en qué compactos podremos integrar). Para ello aplicamos, por ejemplo, el criterio de D'Alembert para el cálculo del radio de convergencia de una serie de potencias, previo cambio de variable t=x2 , ya que la serie anterior no es un desarrollo propiamente dicho (ahora sí). Se trata nada más de un formalismo, pues el radio de convergencia se calcula a partir de los coeficientes de la serie y no de la propia variable, así que esto no influye en nada a los cálculos, pero sí un poco en la conclusión. Veamos: tras el cambio, vamos a calcular el radio de convergencia de la serie
Procediendo como suele hacerse:
siendo
entonces:
es decir, -
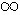< t <
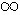+; despejando ahora
x, (donde esté definido) tenemos (también) que
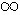- < x <
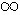+. Por tanto, la serie original es convergente en toda la recta real, en particular es uniformemente convergente sobre los compactos de
, esto nos permitirá
intercambiar el sumatorio con la integral cuando integremos. Vamos ahora a obtener la expresión de la integral entre 0 y un x cualquiera positivo.
Así pues:
y ya podemos calcular esta integral con la precisión que queramos sin más que hallar n acotando el término n+1.
De vuelta a GeoCities