La fórmula de Taylor para varias variables reales

Si f es una función real de clase Cq en un conjunto abierto D de y [a,b] 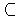D, entonces existe un punto z 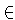]a,x[ tal que

f(x)=Pq-1(a,x-a)+Rq-1(x,a)


donde Rq-1(x,a) es el resto de Lagrange de orden q-1 dado por

y Pq-1(a,x-a) es el polinomio de Taylor de orden q-1:


o bien, agrupando derivadas iguales:

que, formalmente, se escribe:

Sabemos que Pq(a,h) es el único polinomio de grado q que verifica:

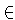
Veamos la expresión del desarrollo de Taylor para el caso n=2 (es decir, si trabajamos con una función de dos variables) en torno a un punto (x0,y0) 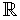2

f(x,y) = f(x0 ,y0) + D1 f(x0 ,y0) (x-x0) + D2 f(x0 ,y0) (y-y0) +
+ ( D1,1 f(x0 ,y0) (x-x0)2 + 2 D1,2 f(x0 ,y0) (x-x0) (y-y0) + D2,2 f(x0 ,y0) (y-y0)2 ) +
+ ( D1,1,1 f(x0 ,y0) (x-x0)3 + 3 D1,1,2 f(x0 ,y0) (x-x0)2 (y-y0) + 3 D1,2,2 f(x0 ,y0) (x-x0) (y-y0)2 +
+ D2,2,2 f(x0 ,y0) (y-y0)3 ) + ...


o, de forma más compacta:


De vuelta a GeoCities