GEOMETRIA AFIN
- Recta que pasa por el punto (a,b,c) y es paralela a los
planos
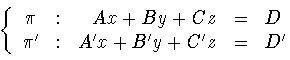
Solución: La recta buscada tiene por ecuación:
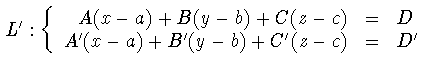
- Proyección del punto (a,b,c) sobre el plano
M:Ax+By+Cz=D en la dirección de
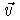 = (i, j, k).
= (i, j, k).
Solución: Construimos la recta L: (x, y, z) = (a, b, c) +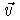 ,
entonces, el punto P' buscado es la
intersección del plano M dado con la recta
L hallada.
,
entonces, el punto P' buscado es la
intersección del plano M dado con la recta
L hallada.
- Proyección de la recta L: (x, y, z) = P +
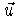 en la dirección del vector
en la dirección del vector
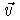 sobre el plano M:Ax+By+Cz=D.
sobre el plano M:Ax+By+Cz=D.
Solución: Construimos el plano M' = P +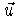 +
+
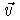 ,
entonces, la recta L' buscada es
L' = M
,
entonces, la recta L' buscada es
L' = M 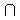 M'.
M'.
- Recta (en implícitas) que pasa por P = (a, b, c)
y se apoya en las rectas L y L'.
Solución: Construir, por una parte, un plano que contenga a L y a P, por otro lado, un plano que contenga a L' y a P. Entonces, hallamos la intersección de ambos planos; esta es la recta buscada. Para hallar el primer plano ( , por ejemplo), usamos
el haz de planos que contienen a la recta L (las ecuaciones
son las de la recta L), sustituyendo el punto en las
coordenadas del haz de planos, así hallamos el
, por ejemplo), usamos
el haz de planos que contienen a la recta L (las ecuaciones
son las de la recta L), sustituyendo el punto en las
coordenadas del haz de planos, así hallamos el
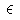 . El otro plano se halla
de la misma forma (con la otra recta, obviamente).
. El otro plano se halla
de la misma forma (con la otra recta, obviamente).
- Recta paralela a L que se apoya en las rectas H
y H' .
Solución: Si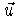 es el vector director
de la recta L , utilizando haces de planos, hallamos el
plano
es el vector director
de la recta L , utilizando haces de planos, hallamos el
plano  que contiene a
H y a
que contiene a
H y a 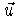 ,
el plano
,
el plano  '
que contiene a H' y a
'
que contiene a H' y a
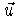 . Entonces, la recta
buscada es la intersección de estos dos plano, i.e.,
. Entonces, la recta
buscada es la intersección de estos dos plano, i.e.,

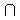
 '.
'.
- Plano que pasa por el punto P y es paralelo a las rectas
L y L' .
Solución: Llamamos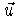 al vector director
de L, y
al vector director
de L, y 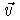 al vector director de L' . Entonces, el plano
al vector director de L' . Entonces, el plano
 buscado tiene la
ecuación vectorial
buscado tiene la
ecuación vectorial
 : (x, y, z) = P +
: (x, y, z) = P +
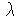
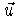 +
+
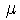
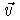
- Recta paralela a los planos
 y
y
 '
que pase por el punto P.
'
que pase por el punto P.
Solución: Hallamos la recta r' intersección de los planos, i.e., r' =
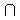
 '.
Entonces, llamamos
'.
Entonces, llamamos
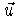 al vector director de esta recta r' (que resulta ser el
producto vectorial de los vectores característicos de
al vector director de esta recta r' (que resulta ser el
producto vectorial de los vectores característicos de
 y
y
 ', otro modo de hallarlo).
Con todo esto, la recta r buscada es r : (x, y, z) = P +
', otro modo de hallarlo).
Con todo esto, la recta r buscada es r : (x, y, z) = P +
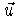
- Plano que contiene a una recta r y es paralelo a otra
recta s.
Solución: Como r está contenida en el plano ,
su vector director (
,
su vector director (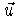 ,
por ejemplo) es un vector generador de
,
por ejemplo) es un vector generador de
 . Como
. Como
 es paralelo a s,
el vector director de s
(
es paralelo a s,
el vector director de s
(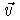 , por ejemplo) es
otro vector generador de
, por ejemplo) es
otro vector generador de  .
Ahora hallamos un punto cualquiera de la recta r (pues
estará en
.
Ahora hallamos un punto cualquiera de la recta r (pues
estará en  ),
llamémosle P. Entonces, la ecuación pedida del
plano es:
),
llamémosle P. Entonces, la ecuación pedida del
plano es:
 : (x, y, z) =
P +
: (x, y, z) =
P + 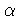
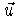 +
+
GEOMETRIA AFIN EUCLIDEA
- Proyección ortogonal de un punto P = (a, b, c)
sobre el plano M:Ax+By+Cz=D
Solución: Lo que debemos hacer es, primero, hallar una recta perpendicular al plano M que pase por el punto P. Con esto, el punto P' es la intersección de dicha recta con el plano. Veamos los pasos con detalle:
- El vector característico de M es
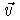 = (A, B, C).
La ecuación de la recta perpendicular a M que pase
por M es:
= (A, B, C).
La ecuación de la recta perpendicular a M que pase
por M es:
L : (x, y, z) = (a, b, c) + v(A, B, C).
De aquí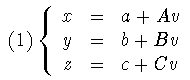
- Sustituyo estas coordenadas en la ecuación del plano:
A(a + Av) + B(b + Bv) + C(c + Cv) = D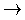 Aa + Bb + Cc + v(A2 + B2 + C2) = D.
Aa + Bb + Cc + v(A2 + B2 + C2) = D.
- Ahora despejo:

- sustituyendo en (1), obtengo las coordenadas del punto buscado,
que son:
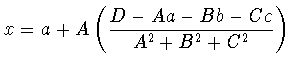
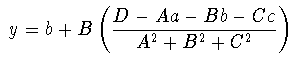
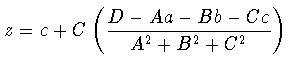
- El vector característico de M es
- Proyección ortogonal del punto P = (a, b, c) sobre
la recta L : (x, y, z) = Q +
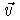
Solución: Construimos un plano perpendicular a L
que pase por el punto P. El vector
perpendicular a L
que pase por el punto P. El vector
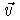 = (i, j, k)
(director de L) es el vector característico del plano,
luego la ecuación de este plano es:
= (i, j, k)
(director de L) es el vector característico del plano,
luego la ecuación de este plano es:
 : i(x-a) + j(y-b) + k(z-c) = 0. Escribimos la recta en
paramétricas, y a partir de ahí, terminamos procediendo
como en el tipo de ejercicio anterior.
: i(x-a) + j(y-b) + k(z-c) = 0. Escribimos la recta en
paramétricas, y a partir de ahí, terminamos procediendo
como en el tipo de ejercicio anterior.
- Hallar la proyección ortogonal de la recta
L : (x, y, z) = (a, b, c) +
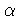 (l, m, n) sobre
el plano M:Ax+By+Cz=D.
(l, m, n) sobre
el plano M:Ax+By+Cz=D.
Solución: Construir un plano perpendicular a M que contenga a L (este plano será M' : (x, y, z) = (a, b, c) +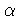 (l, m, n) +
(l, m, n) +
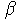 (A, B, C) ).
Entonces, M
(A, B, C) ).
Entonces, M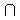 M' = L' nos da la recta buscada.
M' = L' nos da la recta buscada.
- Tengo la recta r y la recta s. Hallar la recta
L perpendicular común a ambas.
Solución:} Si llamamos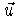 al vector director de la recta r, y
al vector director de la recta r, y
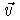 al vector director
de la recta s, entonces el vector director de la recta L
será
al vector director
de la recta s, entonces el vector director de la recta L
será
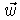 =
=
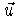
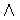
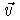 . Ahora hallamos los
planos
. Ahora hallamos los
planos  y
y
 ' usando haces de planos:
' usando haces de planos:
 que contiene a r
y a
que contiene a r
y a 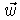 , y
, y
 ', que contiene a s
y a
', que contiene a s
y a 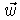 . Entonces, la
perpendicular común es la intersección de los planos
. Entonces, la
perpendicular común es la intersección de los planos
 ,
,
 ' , i.e.,
L =
' , i.e.,
L = 
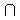
 '
'

De vuelta a GeoCities