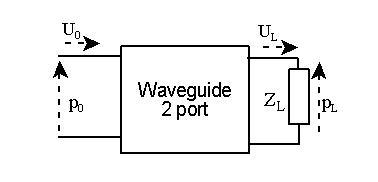
The waveguide model can be used in many ways ....
Consider a waveguide terminated by an acoustical impedance ZL at x=L. This can be modelled by the waveguide two port loaded by a "one port" network representing the termination.....

This system is described by the matrix equation....
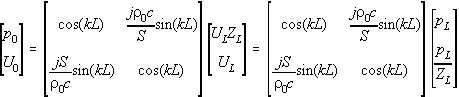
If you don't like matrices, these equations look rather daunting ! However, the real beauty of the technique lies in the fact that any ratio of acoustic variables (i.e. transfer functions, impedances, transfer impedances, etc) can be obtained directly from the matrix equation above.
For example, the input impedance is:
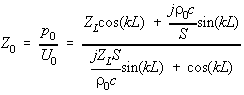
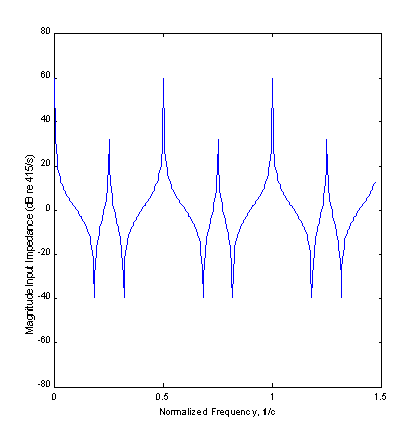
Given appropriate functions (available from me) this input impedance can be obtained from the chain matrix and the load impedance in a single line of MATLAB code ! The magnitude input impedance is shown below when the load is.. i) characteristic (shown in red) ii) 1000 times characteristic (shown in blue) iii) 1/1000 times characteristic (shown in black)
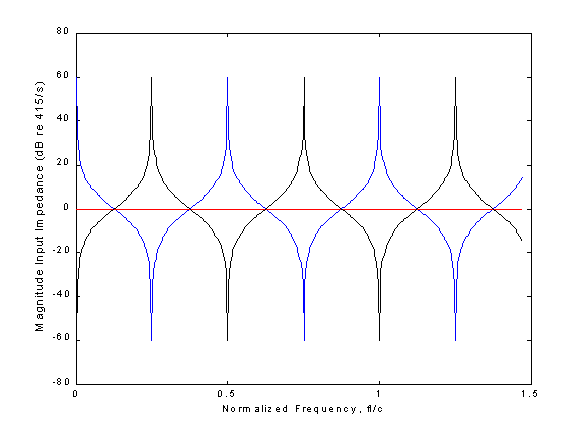
The frequency axis is labelled in units of length / l (i.e. a value of 1 corresponds to the case when the wavelength equals the pipe length) You can clearly see the family of half-wave resonances when the termination impedances is high (shown in blue) and the family of quarter-wave resonances when the termination load is low (shown in black).
Connecting two waveguide segments together is trivial when the cross sectional areas are equal, as it simply changes the length. However, the method still works.....
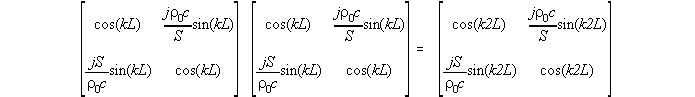
Joining pipe segments of different cross sections is much more interesting, as the impedance change generates reflections.
Consider the following system, comprised of two waveguide segments, terminated by a load.....
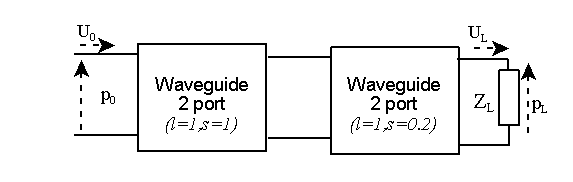
Given appropriate functions (available from me), the two waveguide matrices (formed from this code) and the termination load, the input impedance can be obtained in two lines of MATLAB gode ! What other method could give the result shown below so quickly ? Note: ZL=415000/s