The loudspeaker model can be used in many ways ....
Consider a loudspeaker driving a waveguide of area equal to the cone area, terminated by an acoustical impedance ZL at x=L....

The central matrix converts the velocity output of the loudspeaker to the volume velocity input to the waveguide. This system is described by the matrix equation....
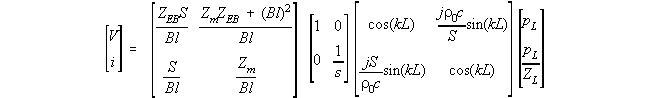
This equation is easy to solve for the ratios of any two electrical or acoustical variables.
For example, a conventional loudspeaker with the following parameters... cone radius = 0.06 m Motor factor Bl = 5 W/m resistance = 8 W inductance = 0.5 mH Mass = 0.01 kg Stiffness = 2000 N/m Damping = 0.1 Ns/m driving a 1 metre duct, produces the following pressure response....
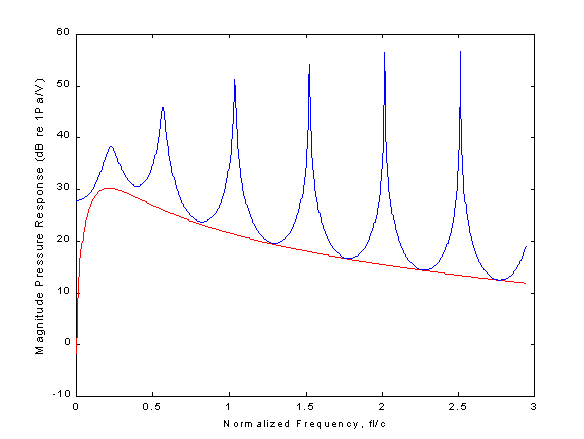
Given appropriate functions (available from me) these pressure responses can be obtained from the chain matrices of the speaker (this code), the waveguide (this code), and the load impedance in three lines of MATLAB code ! How would you try to analyse the system ? The red trace shows the pressure response obtained when the duct is characteristically terminated (unlike conventional loudspeaker loadings, the pressure response is never flat in this application due to the changing source impedance of the 'speaker). The blue trace shows the pressure response obtained when the duct is terminated by a high impedance (415000/s). At low frequencies the resonances are clearly NOT on the halfwave resonances as the 'speaker's source impedance is quite low. At higher frequencies the resonances start to line up with the half wave frequencies.
The two port methods can be used to study more complicated aspects of loudspeaker operation.
You can model