Empowered Investor

In another section of this site, we discussed the procedure for choosing the best investment based on risk and yield. That choice is controlled by two quantities - accumulation and DQPY (Down Quarters Per Year). However, putting all your money in that best investment is equivalent to the proverbial "putting all eggs in one basket".

What will you learn in this section?

1. Benefits of diversification.
2. Maximizing accumulation through asset allocation.

Allocation

A portfolio consists of several investments. The fraction of the total asset invested in each investment is the allocation in that investment. If you invest 25% of your asset in PPX, 40% in QQX, and 35% in RRX, then the allocations in PPX, QQX, and RRX are 0.25, 0.40, and 0.35, respectively. Denoting these allocations by F_P, F_Q, and F_R, you would find that

Equation (1) means that the sum of the allocations gives the whole portfolio or "one". In general, if you have N number of investments with allocations of F₁, F₂,...,F_N, then

F_I = 1 . . . Equation (2)

Yield

If you know the average yields from each investment, then you can calculate the average yield of the portfolio. Say, the yields from PPX, QQX, and RRX are Y_P, Y_Q, and Y_R, respectively. Then, the average yield Y of the portfolio is given by

In general, for N number of investments with yields of Y₁, Y₂,...,Y_N

Y = Y_IF_I . . . Equation (4)

Variance and Risk

To calculate risk, you need to calculate two statistical quantities - variance and co-variance. The procedure for calculating these quantities by using Excel is given later in this page.

Variance is a measure of the fluctuation in the yield of an investment. For PPX, QQX, and RRX, we will denote the variances by V_P, V_Q, and V_R

Co-variance is a coupling between the fluctuations in the yields of two investments. For PPX, QQX, and RRX, we can calculate three such couplings. These couplings are denoted by C_PQ, C_PR, and C_QR. Note the double subscript of C that identify the coupling.

The variance V of the portfolio can now be written as

In general, for a portfolio with N investments, the variances are denoted by V₁, V₂,...,V_N, and the covariances by C₁₂, C₁₃,...,C_IJ,...,C_N-1,N

Then the variance of the portfolio is

V = F_P²V_P + C_IJF_IF_J . . . Equation (6)

As discussed in the page on Risk and Yield, the risk is the square-root of the variance.

Optimum Portfolio

In a portfolio with N number of investments, the allocations F₁, F₂,...,F_N, the yield Y, and the variance V are related through the equations (2), (4), and (6). The purpose of optimization is to minimize V for a given Y by suitably choosing the allocations. The problem statement for the optimization reads as follows: For a given yield Y = Y₀, find F₁, F₂,...,F_N such that V is minimized. If you are not allowed to "short" any of the investments, then you must do a constrained optimization. The constraints are:

This constrained optimization problem can be conveniently solved by using Excel. The procedure for Excel is demonstrated later in this page.

For now, we leave the abstract mathematics and focus on a concrete example.

Consider three investments with tickers AAA, BBB, and ZZZ. In Table I, the annual yields from these three investments are shown over a five-year period.

In Table II, the average yield, risk, expected growth of $1 over a one year period, and the DQPY are shown.

Obviously, AAA is the best investment, because it has the largest accumulation potential. Although the first impulse is to put all our money in AAA, but the reality dictates that, a mixture of AAA and ZZZ gives us a better portfolio than AAA alone. This mixing of investments is diversification.

We now explore the reason behind the advantage of mixing investments. In the plot below, the variations of yield with time for AAA, BBB, ZZZ are shown.

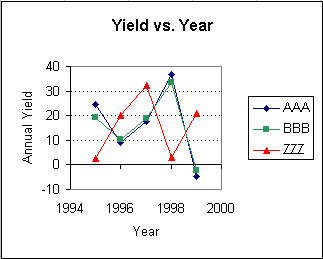
This plot shows that, the yields of AAA and BBB are in phase, i.e., the yields of AAA and BBB go up and down together. Whereas, the yield of ZZZ is out of phase with the yields of AAA and BBB, i.e. when ZZZ is up, AAA and BBB are down and vise versa. In mathematical terms, ZZZ has a negative covariance with AAA and BBB. Whereas, AAA and BBB have a positive covariance among themselves.

In the market place, you will find many pairs of investments with negative covariance; examples are: value and growth, domestic and international, small-cap and large-cap, European stocks and Asian stocks, etc. It is not necessary that this negative covariance persists continually. Even occasional negative covariance is good enough reason for diversification, as will be shown below. Intuitively, mixing two out-of-phase investments makes sense, because when one is not making money the other is.

Two other quantities you need for the diversification calculation are: the variances and the average yields of AAA, BBB, and ZZZ. You may recall that the variance is the square of the risk (SD)

What is asset Allocation?

Consider a portfolio with 40% of the capital invested in AAA, 35% in BBB, and 25% in ZZZ. The fractions 0.40, 0.35, and 0.25 are the allocations in the three investments. We denote the allocations in AAA, BBB, and ZZZ by F_A, F_B, and F_Z, respectively.

Why should you do asset allocation?

The purpose of asset allocation is a diversification of asset. Asset allocation increases the rate of growth of your capital by minimizing risk. Through asset allocation, an investor makes up the loss (or low yield) in one investment, over certain periods of time, by the better gain in another investment.

If diversification is the goal, why not Index investing?

Index investing is a diversification strategy of investing in a large number of stocks. There are many standard index investing tools available in the market, such as DOW 30 (30 stocks), S&P 500 (500 stocks), Russell 2000, and Willshire 5000. The allocation of capital in each stock in these Indices is based upon the size of the company. However, this allocation may not be right for you.

What is the difference between diversification and asset allocation?

Diversification is only one part of asset allocation. Diversification reduces risk, but asset allocation minimizes risk for a given yield. In that sense, an asset allocated portfolio is optimized. As will be shown below, the best reduced risk portfolios are constructed by mixing investments that have negative covariance among them.

Is this optimum portfolio same for everybody?

Absolutely not. The optimization depends on need. For example, a young investor seeks growth of capital and not income; whereas, a retiree may pay more attention toward income. Need-based optimization is a more difficult problem and will be addressed in a future section.

In Table II, we calculated the expected accumulations if we invest in only one of the three choices: AAA or BBB or ZZZ. Now, we would examine the effect of mixing investments in a portfolio. Let us consider two portfolios:

1. Combination of AAA and BBB. In this portfolio, F_A is the fraction of asset in AAA and F_B is the fraction of asset in BBB.
2. Combination of AAA and ZZZ. In this portfolio, F_A is the fraction of asset in AAA and F_Z is the fraction of asset in ZZZ.

Portfolio AB

If we put all our money in AAA (F_A=1, F_B=0), then from Table II, our expected yield is 16.72% and risk is 15.57%. On the other hand, if we put all our money in BBB (F_A=0, F_B=1) then from Table II, our expected yield is 15.96% and risk is 13.16%. Thus, the expected yield of Portfolio-AB is bounded by 16.72% at the top and 15.96% at the bottom. All mixtures of AAA and BBB give average yields within this range of the expected yield. Any such mixture would be beneficial to us only if we can reduce the risk.

In mathematical terms, we solve an optimization problem. The procedure for optimization is as follows:

• Step 1: Pick an average yield within the available range (between 15.96% and 16.72%).
• Step 2: Find the allocation in AAA, F_A, and the allocation in BBB, F_B, such that the risk is minimum for the yield desired in Step 1.

We can pick various yield values in Step 1 and run the optimizer of Step 2 for each of these yields. The results of such an exercise are shown in Table III. The quantity Y_AB is the yield of AB-Portfolio.

The optimizer is available within the Excel software in your computer. I will show you how to run the optimizer and I will give you the mathematical details of the optimizer, later in this page. For the time being, let us examine Table III.

Table III shows:

1. As higher yield is demanded from the portfolio, optimization requires bigger allocation in AAA.
2. Investment AAA being more risky, the risk increases with demanded yield.
3. DQPY monotonically increases with demanded yield.
4. Initially, increasing risk gives bigger accumulation, as in the first five rows of the table.
5. Eventually, higher yield and higher risk saturates the accumulation. Beyond this saturation, higher yield and risk do not fetch higher accumulation.
6. Beyond the fifth row of the Table, the accumulation remains constant while the DQPY continues to increase.

The outcome of this analysis is graphically shown in the following Figure. The plot shows a steep rise in risk for small increases in the yield.

Based on the values of accumulation and DQPY, the best possible allocation in the AB-Portfolio is 64% in AAA and 36% in BBB. The accumulation value is 1.155 and DQPY value is 0.48.

An important observation: When you mix two investments that are in positive covariance (such as AAA and BBB), do not expect vastly improved performance from your portfolio. But, as will be shown below, when you mix investments that are in negative covariance (such as AAA and ZZZ), amazing results can be achieved through optimization.

Portfolio AZ

If we put all our money in AAA (F_A=1, F_Z=0), then from Table II, our expected yield is 16.72% and risk is 15.57%. On the other hand, if we put all our money in ZZZ (F_A=0, F_Z=1) then from Table II, our expected yield is 15.82% and risk is 12.76%. Thus, the expected yield of Portfolio-AZ is bounded by 16.72% at the top and 15.82% at the bottom. All mixtures of AAA and ZZZ give average yields within this range of the expected yield. Any such mixture would be beneficial to us only if we can reduce the risk.

The results of the optimization process for Portfolio-AZ are shown in Table IV. The quantity Y_AZ is the yield of AZ-Portfolio.

Table IV shows:

1. As higher yield is demanded from the portfolio, optimization requires bigger allocation in AAA.
2. At the beginning, risk decreases with yield. After the risk reaches a minimum, it begins to rise with yield.
3. At the beginning, DQPY decreases with yield. After DQPY reaches a minimum, it begins to rise with yield.
4. Initially, decreasing risk and increasing yield give bigger accumulation, as in the first five rows of the table.
5. Eventually, higher yield and higher risk saturates the accumulation. Beyond this saturation, higher yield and risk do not fetch higher accumulation.

The outcome of this analysis is graphically shown in the following Figure. Note the decreasing risk with increasing yield at the beginning. After risk hits a minimum, risk and yield rise together. The bullet shaped risk-yield curve for optimized portfolios is called the efficient frontier.

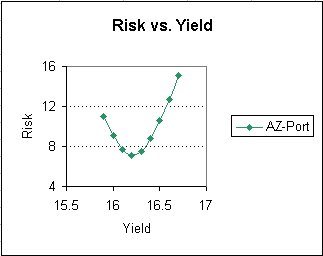
Based on the values of accumulation and DQPY, the best possible allocation in the AZ-Portfolio is 53% in AAA and 47% in ZZZ. The accumulation value is 1.161 and DQPY is 0.06.

Summary

We started with three choices of investment - AAA, BBB, ZZZ. First, we constructed a portfolio consisting of only one investment AAA. Second, we constructed portfolio AB and finally, we constructed Portfolio-AZ. The outcomes from these three choices are summarized in Table V, below. In constructing Table V, we have hypothesized the following situation: $20,000 is invested for a period of 10 years.

Comments: (i)The portfolio containing 100% AAA is the worst. (ii) Combining AAA and BBB provides some advantage as the number of "down quarters" is reduced. However, we do not gain anything in accumulation. This was somewhat expected as AAA and BBB have positive covariance. (iii) Combining AAA and ZZZ provides astonishing results. The accumulation goes up by $4500 and at the same time the number of "down quarters" goes down to 1. This shows that an optimized mixture of two investments in negative covariance leads to higher accumulation and lower risk. Asset allocation benefits the investor in two ways - higher gains and lower probability of loss of capital.

The Equations

In order to write the mathematical equations for Asset Allocation among investments, we need to introduce some symbols.

• Y_A, Y_B, Y_Z are the average yields of AAA, BBB, ZZZ, respectively.
• V_A, V_B, V_Z are the variances of AAA, BBB, ZZZ, respectively.
• C_AB, C_AZ , C_BZ are the covariances of AAA and BBB, AAA and ZZZ, and BBB and ZZZ, respectively.

In Table V, the values of all of these quantities are given.

In the AAA and BBB portfolio, the fractions of assets in AAA and BBB are F_A and F_B, respectively. The variance (risk squared) of the portfolio, V_AB, is given by

Our goal is to minimize the variance, V_AB, for the portfolio under certain conditions. The conditions are:

Data Entry

• Step 1: Store V_A and V_B in cells A1 and A2.
• Step 2: Store C_AB in cell B1
• Step 3: Enter guessed values for F_A and F_B in cells C1 and C2. Any guessed value can be chosen; I always enter zero for guess.
• Step 4: Enter values for Y_A and Y_B in cells D1 and D2.
• Step 5: Type in the expression on the right-hand-side of Equation (8) in cell A5 as follows: =C1^2*A1+C2^2*A2+2*C1*C2*B1.
• Step 6: Type in the expression on the left-hand-side of Equation (9) in cell B5 as follows: =C1+C2.
• Step 7: Type in the expression on the right-hand-side of Equation (10) in cell C5 as follows: =C1*D1+C2*D2.
• Step 8: Enter the desired yield in cell D5. This yield must be in the designated range (see discussion on Portfolio-AB, above).

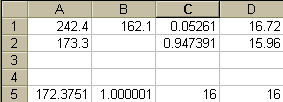
  After these eight steps, the Excel sheet will look like the Figure below. The demanded yield of 16% is entered in cell D5.

  
• Step 9: Pull down the Tools Menu and click on "Solver". You will get a pop-up window. Enter the following information in the pop-up:
  • Set Target Cell: A5
  • Click radio button "Min"
  • By Changing Cells: C1, C2.
  • Enter following constraints in the "Subject to the Constraints Box", by clicking the Add button for each constraint:
    • B5 = 1
    • C5 = D5
    • C1 >= 0
    • C2 >= 0

At the completion of these steps, the pop-up window will appear as shown in Figure below.

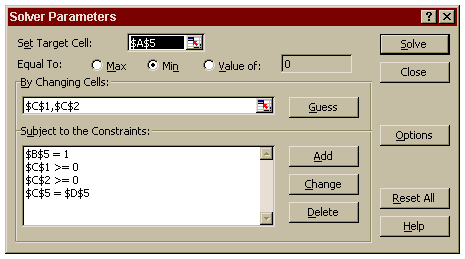
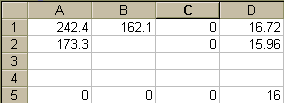
Now, click the "Solve" button. The optimized allocations for AAA and BBB will appear in cells C1 and C2. Repeat the calculation after entering a new desired yield in cell D5.

The following Figure shows the Excel screen after the solver has found the optimum allocation. In this Figure, the demanded yield of 16% is in cell D5, the optimized yield of 16% is in cell C5, the optimum allocations appear in cells C1 and C2, and the minimized variance of 172.4 appear in cell A5.