Sections: Power | Impedance | Students Challenge

Unsymmetrical Series Impedance

Definition.

Assuming that there is no coupling, i.e., no mutual inductance between the impedances, thus the voltage drop would be:

Multiplying both sides by the unit matrix of a, we have:

, where: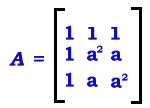

To eliminate the A matrix on the right side,
we should multiply it with A^-1, where this is equal to:

Thus, the voltage equations will be:
V_aa'1 = (I_a1/3) (Z_a+Z_b+Z_c) + (I_a2/3) (Z_a+a²Z_b+aZ_c) + (I_a0/3) (Z_a+aZ_b+a²Z_c)
V_aa'2 = (I_a1/3) (Z_a+aZ_b+a²Z_c) + (I_a2/3) (Z_a+Z_b+Z_c) + (I_a0/3) (Z_a+a²Z_b+aZ_c)
V_aa'0 = (I_a1/3) (Z_a+a²Z_b+aZ_c) + (I_a2/3) (Z_a+aZ_b+a²Z_c) + (I_a0/3) (Z_a+Z_b+Z_c)

Important Notes.
1. If Z_a = Z_b = Z_c then: V_aa'1 = I_a1Z_a V_aa'2 = I_a2Z_a V_aa'0 = I_a0Z_a
2. If mutual inductance exist, then the impedance square matrices of the above equations [voltage drop equation and the equation multiplied by the A-matrix] would contain off-diagonal elements and the last set, the voltage equations, would contain additional terms.

---

Sections: Power | Impedance | Students Challenge

Students Challenge

Assignment
Solve the following problems:
No. 11.6/p.303
No. 11.7/p.303
No. 11.8/p.303