Electrical Machine Design

WEEK 07: TRANSFOMERS: CALCULATIONS & TEST DATA

Stampings.
Alloyed iron and silicon-steel are used for cores. Stampings usually employ either 29-gage (0.014 in.) or 26-gage (0.0185 in.) straight pieces. Usual thickness for 25 to 60 hz, is the 29-gage stampings. Varnish is provided for insulation between laminations and reduce eddy currents loss.

Space Factor.
This is the ratio between cross section of copper in a given space and the total cross section including insulation and air or oil spaces.

The space factor, sf can be approximated by using: sf = 10 / (30 + kV) where kV is the kilovolts at high tension. This approximation is only applicable for 50 to 200 kVA. Add 20% for ³ 1,000 kVA, and subtract 20% for £ 7.5 kVA.

Window

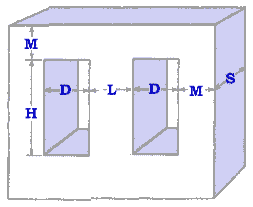Shell-Type Window.

H x D = 2 x (TI) / (D x sf)

Where:
H » 2.5 to 3.5 x D
S » 2.0 to 3.0 x L
M » 0.5 to 0.75 x L

Usually M is made greater than 0.5L so that the length per turn of winding is small by forcing the flux density to high values inside the core, but low flx values (to avoid iron loss) in the portion of magnetic circuit outside the coils.

Core-Type Window.

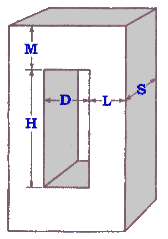
H / D » 2.5 to 3.5

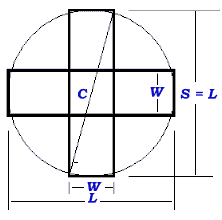
Gross Area of
Cross Section:
2WL - W²

By maxima/minima
differentiate:
2 (W dL/dt + L) - 2W = 0
but W² + L² = C²,
2W dW + 2L dL = 0, thus -w/L = dL/dW

Substituting to original equation:
[W (-W/L) + L] - W = 0
-W²/L + L - W = 0
W² + WL - L² = 0
by approximation:
W = 0.618 L and W = 0.575C, L = 0.85C.

For one-step cruciform section:
a = tan^-¹(W/L) = 31.7°
b = tan^-¹(L/W) = 58.3°

For two-step cruciform section:
a = 25.7° b = 45.7° g = 54.3°

For three-step cruciform section:
a = 21.9° b = 38.3° g = 53.5° d = 68.1°

Net Cross section is the product of the Gross section and the stacking factor. The stacking factor for cruciform is usually between 0.86 to 0.90, if there are no air or oil ducts between sections.

For large transformers, ducts should be ¼ to ½ in.
for small transformers, especially rectangular cores, initial values of the dimensions can be obtained through S = 1.5L, H = 2.5D, M = 1 ~ 1.5 L.