Una vez que se conoce la función de transferencia del sistema y se ha resuelto la función del regulador, éste ha de implementarse con una tecnología, que puede ser tan variada como los tipos de sistemas a regular, por ejemplo sistemas mecánicos, fluidos, electrónicos, eléctricos..., pero no cabe duda que la electrónica analógica y la digital son las más comunes hoy en dia, especialmente los reguladores industriales y los dispositivos programables como microcontroladores, autómatas y ordenadores.
Ya se trató el tema de los reguladores industriales, casi siempre PIDs, cuyos parámetros de ajuste se determinan con la función de transferencia del regulador, siempre y cuando sea posible la regulación con una de las configuraciones típicas del PID. Un PID también puede encontrarse ya programado, en subrutinas o bloques de programa, en la mayor parte de los autómatas industriales de gama media y alta. Es este caso se implementa por asignación de valores a los parámetros, definidos en el bloque o subrutina de regulación.
La alternativa de los amplificadores operacionales puede ser un recurso económico en comparación con otros sistemas. Necesita la electrónica de alimentación, varios amplificadores operacionales y unos pocos componentes de ajuste y amplificación.
Los ordenadores tienen la desventaja de un diseño que se adapta con dificultad a la comunicación con el proceso, ya que sus puertos están pensados para conectar periféricos de tipo informático. Una comunicación a nivel de sensores y control de accionadores de un proceso, hace necesario añadir algún tipo de tarjeta de adquisición o intercambio de datos, un software controlador de la tarjeta y otro de programación de los algoritmos de regulación y del interface gráfico.
Los microcontroladores tienen la desventaja de que su programación es más compleja, porque solo disponen de un reducido número de instrucciones y se necesita una infinidad de instrucciones para programar una aplicación muy simple. También necesitan la electrónica destinada para su alimentación y amplificación de señales. Es necesario conocer su estructura de memoria y los modos de acceso a la misma. Si se desea una supervisión informática, es necesario establecer un enlace con un PC que, en el mejor de los casos, ya existe en el microcontrolador, pero exige programar tanto el PC como el microcontrolador, respetando un protocolo de transferencia y recepción.
Los autómatas programables están en un nivel intermedio. Se adaptan con facilidad al proceso, su programación es simple, y se conectan con facilidad a ordenadores en caso de necesitar una supervisión informática. Su velocidad de proceso es cada vez mayor y en la mayor parte de los casos será suficiente. El autómata elegido para la maqueta, siendo de gama baja, ha permitido un tiempo de muestreo de 4 milisegundos, es decir, 250 ejecuciones del programa de regulación por segundo. Su diseño modular se adapta con facilidad a los procesos y a las comunicaciones con otros sistemas, gracias a las tarjetas de ampliación, como por ejemplo de entradas y salidas analógicas y de comunicaciones. Los programas SCADA (software de control y adquisición de datos) facilitan la supervisión informática a través de una conexión de red, que los fabricantes han previsto para la mayor parte de los autómatas del mercado. Los propios fabricantes de autómatas suelen tener su versión de SCADA particular. En conclusión, se trata de la solución más flexible y más exenta de complicaciones y de gastos de tiempo, pero, como es lógico, se paga más caro.
Aunque las funciones de transferencia reflejan la dinámica de los procesos y sus reguladores, no tienen nada que ver con la respuesta en función del tiempo, que se necesita conocer para implementar los reguladores. Existe una transformación matemática, llamada transformada de Laplace, que hace la conversión entre respuesta temporal y función de transferencia, y también, a la inversa, convierte funciones de transferencia en respuesta temporal. Sin embargo, aquí se ha preferido utilizar una analogía eléctrica tan sencilla como la ley de Ohm.
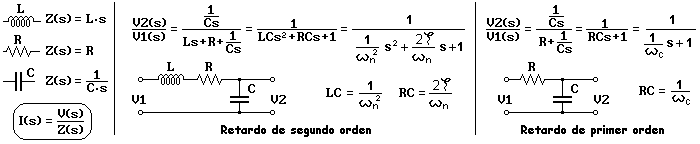
Una bobina no se opone al paso de una intensidad de corriente constante, pero si la intensidad aumenta o disminuye, la bobina se opone a la variación, generando una diferencia de potencial entre sus extremos que es proporcional a la rapidez con la que varía la corriente. Por lo tanto, la tensión es proporcional a la derivada de la intensidad, siendo la constante proporcional el coeficiente de autoinducción de la bobina (L), que se mide en henrios. La función de transferencia de la bobina será L·s, ya que existe un comportamiento proporcional (factor L) y un comportamiento derivativo al que corresponde una función de transferencia igual a "s". Por otra parte, como la función de transferencia representa la ganancia del componente, que será el cociente entre la tensión que genera la bobina y la intensidad que recibe, coincide con el concepto de impedancia y por esta razón, impedancia compleja y función de transferencia son equivalentes.

La impedancia de una resistencia pura es su resistencia R en ohmios, siendo R su impedancia compleja. En el caso de un condensador, tendrá una carga eléctrica igual a la intensidad de corriente que acumula. La tensión entre los extremos del condensador será mayor cuando mayor sea su carga y será menor cuanto mayor sea su capacidad C, que se mide en faradios. Por lo tanto, la tensión en los extremos de un condensador es igual al cociente entre su carga y su capacidad. Como la carga es la intensidad que acumula (una integral), resulta una impedancia compleja (o función de transferencia) igual a 1/C·s, siendo 1/C un factor proporcional y 1/s un integrador.
En la figura anterior se han determinado las funciones de transferencia de los circuitos LRC y RC, aplicando simplemente la ley de Ohm con las impedandias complejas, como si se tratara de resistencias puras en corriente continua. Las funciones han resultado ser un retardo de segundo orden (polinomio de segundo grado en el denominador) y un retardo de primer orden (polinomio de primer grado en el denominador). Puesto que se conocen las funciones de estos retardos en función de la frecuencia natural, relación de amortiguamiento y frecuencia de cruce, queda definida su equivalencia con los valores de L, R y C.
Una forma de implementar físicamente los retardos de primero y segundo orden se deduce de la figura anterior, seleccionando los valores de resistencia (en ohmios), inductancia (en henrios) y capacidad (en faradios), necesarios para conseguir la frecuencia natural y relación de amortiguamiento deseados, o bien la frecuencia de cruce deseada. No obstante, esto puede aplicarse solamente si la señal de respuesta (V2) se aplica a un circuito con elevada impedancia de entrada, pues en caso contrario aumenta el consumo de corriente y falsea la respuesta. Este inconveniente se tratará más adelante, cuando se complete la implementación de reguladores con amplificadores operacionales.
Bloque proporcional. Su respuesta se programa simplemente como el producto de la entrada por la ganancia K del bloque:
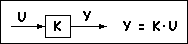
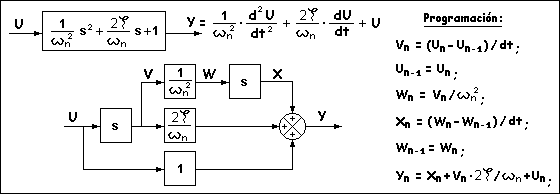
Bloque derivativo.Su respuesta es la derivada de la señal de entrada, igual a la pendiente de la gráfica de la entrada U en función del tiempo. Si se considera un instante de tiempo, llamado "diferencial de t" (dt), éste se corresponde con una variación de U, llamada "diferencial de U" (dU). El cociente dU/dt coincidirá con la pendiente de la gráfica si dt tiende a cero. En la práctica, se programa con incrementos de tiempo (dt) muy pequeños, que, aunque no tienden a cero, sí son lo bastante pequeños como para conseguir una aproximación a la derivada muy buena. El valor dt será el tiempo de muestreo (tiempo que transcurre entre dos lecturas consecutivas del valor de la entrada U), expresado en segundos, y normalmente será del orden de milisegundos (1 ms = 0.004 seg). Por lo tanto, siendo "n" el número de muestreo, la respuesta "Y" se programa como indica la siguiente figura. Dado que se necesita el valor de U del muestreo anterior (n-1), es necesario registrar Un como Un-1 para que esté disponible en el muestreo siguiente.

Bloque doblemente derivativo. Equivale a dos bloques derivativos en serie y su programación se hace ejecutando dos veces las operaciones que se acaban de ver. En la figura, la señal V intermedia es la respuesta del primer bloque y se aplica como entrada del siguiente bloque. En cada muestreo, es necesario registrar Un como Un-1 y registrar Vn como Vn-1 para que estén disponibles en los cálculos del siguiente muestreo.

Bloque integrador (un polo en el origen). Su respuesta es la integral de la señal de entrada U, igual al área bajo la gráfica de la señal de entrada. Para cada muestreo, la respuesta Yn será igual al área añadida desde el muestreo anterior, sumado al área acumulada hasta ese instante (Uac). El área añadida desde el muestreo anterior se calcula como el área de un rectángulo de anchura "dt" (tiempo de muestreo) y altura "Un". El error es muy pequeño porque "dt" también lo es. La suma indicada será el nuevo área acumulada, por lo que es necesario recordar su valor para el muestreo siguiente, guardando el resultado como Uac.

Factor de primer orden (un cero en el eje real). Puesto que su función de transferencia contiene una suma, su diagrama de bloques de descompone en dos ramas en paralelo, siendo la rama superior igual a la conexión en serie de un bloque proporcional y otro derivativo. Si las señales intermedias se nombran como V y W, la programación se obtiene fácilmente como se ha visto para los bloques individuales...

Factor de segundo orden (dos ceros conjugados). Aunque la doble derivada aparece después que el inverso del cuadrado de la frecuencia natural, el orden de los bloques en serie no importa, por lo que uno de los bloques derivativos puede colocarse primero. Haciendo lo mismo con la derivada en el segundo sumando, quedarían dos bloques derivativos que recivirían la misma señal de entrada (U) y devolverían igual respuesta. Por lo tanto, éstos dos bloques se reducen a uno solo y su respuesta se descompone en las dos ramas superiores, de esta forma se reduce un poco el número de cálculos. Del diagrama se deducen las operaciones a programar como ya se sabe de los casos anteriores...
Retardo de transporte. Su respuesta es igual al valor de entrada existente un determinado tiempo atrás, igual a tau en segundos. Su programación implica el registro en una lista de datos de todos los valores de U en muestreos anteriores, comprendidos desde un tiempo tau anterior, hasta el instante actual. En cada muestreo, la respuesta "Yn" se iguala al dato más antiguo, se elimina ese dato de la lista y se añade a la lista el valor actual de la entrada. Sin embargo, no tiene interés práctico en la programación de reguladores porque no se añade nunca en un regulador, ya que este comportamiento siempre es perjudicial.
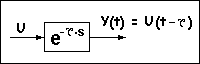
Retardo de primer orden (un polo en el eje real). En la primera columna de la siguiente figura se repite la función de transferencia del circuito RC que, como se explicó en el apartado sobre impedancias complejas, se comporta como un retardo de primer orden en el que la inversa de la frecuencia de cruce es igual al producto de la resistencia por la capacidad del condensador. El condensador tendrá una carga eléctrica que aumentará mientras reciva intensidad, es decir, la carga es "la intensidad eléctrica que acumula el condensador" (Iac) y se representa como la integral de la intensidad. La tensión entre los extremos del condensador (V2) será mayor cuanto mayor sea la carga (la integral) y será menor si la capacidad del condensador es grande (inversamente proporcional), ya que sucede como con el nivel de líquido en un depósito de grandes dimensiones, el nivel es mayor cuanto mayor sea su carga o volumen de agua, pero será más pequeño cuanto mayor sea la sección del depósito.
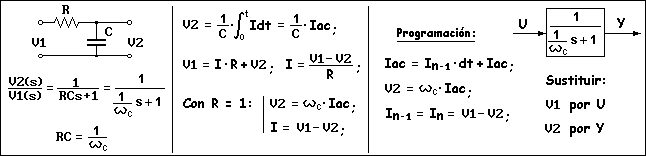
La tensión que se aplica como entrada del circuito (V1) será la suma de la tensión entre los extremos de la resistencia (I·R) y la tensión entre los extremos del condensador (V2). Despejando la intensidad, quedará como la diferencia entre V1 y V2, dividido entre la resistencia. Teniendo en cuenta que en un retardo de primer orden solo existe como parámetro la frecuencia de cruce y en el circuito RC existen dos parámetros (R y C), uno de ellos puede tomar cualquier valor, de modo que si la resistencia R se considera igual a 1, resulta que R·C = C = inversa de la frecuencia de cruce. Por lo tanto, la inversa de C es igual a la frecuencia de cruce y V2 será igual al producto de la frecuencia de cruce por la intensidad acumulada (Iac). Igualmente, la intensidad queda como la diferencia de tensiones V1 y V2.
La programación es sencilla: Se comienza calculando la intensidad acumulada (Iac) como se hace con toda integral, es decir, añadiendo el incremento actual (I·dt) al valor acumulado hasta el momento (Iac). Con la intensidad acumulada y la frecuencia de cruce ya se puede calcular la señal de salida (V2) y, por último, se calcula la intensidad actual (In) y se registra como In-1 porque se necesitará en el siguiente muestreo para calcular Iac. Aunque se ha considerado como entrada V1 y como salida V2, que representan tensiones, no hay diferencia con otros tipos de variables si se cambia V1 por otra entrada U y V2 por otra salida Y.
Retardo de segundo orden (dos polos conjugados). En la primera columna de la siguiente figura se repite la función de transferencia de un circuito LRC que, como se explicó en el apartado sobre impedancias complejas, se comporta como un retardo de segundo orden en el que la frecuencia natural y relación de amortiguamiento tienen una relación con los valores de inductancia L, resistencia R, y capacidad C. La tensión de salida V2 es, como en el caso anterior, igual a la intensidad acumulada (Iac) dividido entre la capacidad del condensador. La tensión V1 es la suma de las caidas de tensión: En la bobina, en la resistencia y en el condensador. Toda bobina se opone siempre a las variaciones de corriente que la atraviesan, pero no opone resistencia si la corriente que la atraviesa se mantiene constante. Por lo tanto, la bobina origina una caida de tensión proporcional a la rapidez con la que varía la intensidad, que es la derivada de la intensidad respecto del tiempo. La constante de proporcionalidad es el coeficiente de autoinducción de la bobina (L) y se mide en henrios. Por último, despejando la intensidad y dando a R el valor 1, quedan fijadas las fórmulas de cálculo necesarias para programar el retardo de segundo orden.

Como en el caso anterior, la programación comienza calculando la intensidad acumulada y la señal de salida (V2). Seguidamente se calcula la intensidad (In), en cuyo cálculo interviene la derivada de la intensidad, pero como In todavía no se conoce, ha de calcularse la derivada con las intensidades de los dos muestreos anteriores. Por último, el valor de In-1 pasa a In-2 y el valor de In pasa a In-1, ya que en el siguiente muestreo se necesitan para calcular Iac y el siguiente valor de In. Como es lógico, si la entrada y salida no son tensiones, bastará con cambiar V1 y V2 por las correspondientes señales de entrada y salida.
Conclusiones sobre programación de reguladores:
Toda función de transferencia de un regulador, descompuesta en factores, se programará mediante cálculos similares a los que se han descrito para cada tipo de bloque, encadenando la salida de uno como entrada del siguiente. Es conveniente, antes de comenzar la ejecución de los cálculos, definir las variables que se necesiten como registros de valores de muestreos anteriores. Estas variables deben ser globales, es decir, definidas fuera del procedimiento o subrutina en la que se programen los cálculos, ya que en caso contrario se pierden cuando finaliza el procedimiento y no estarán disponibles para la siguiente ejecución.
El procedimiento o subrutina que contenga los cálculos ha de ser ejecutado en intervalos de tiempo (tiempo de muestreo dt) lo más cortos que sea posible, a fin de que las variaciones de medida no puedan ser demasiado grandes en dicho tiempo de muestreo. Si el dispositivo programable lo permite, es mejor que el tiempo de muestreo sea constante, lo que hará innecesario medir los tiempos entre cada ejecución y se garantiza un comportamiento más regular, ya que si las ejecuciones ocurren con dependencia de las tareas que ejecuta el sistema programable, es posible que los tiempos de muestreo resulten muy irregulares, disminuyendo así la precisión en los cálculos.
Tiempos de muestreo uniformes se consiguen normalmente mediante interrupciones temporizadas, cuya programación depende, lógicamente, del dispositivo programable que se utilice. De esta forma, cada vez que se cumple el tiempo programado, el sistema detiene su trabajo y ejecuta el procedimiento o subrutina que hayamos asignado a la interrupción temporizada. Por otra parte, si se define un tiempo de muestreo demasiado pequeño, es posible que se acumulen interrupciones pendientes hasta terminar apareciendo fallos, pero incluso con tiempo suficiente, el sistema también necesita, entre interrupción e interrupción, ejecutar otras tareas programadas y tareas de sistema. Si no le resulta posible, terminará igualmente apareciendo fallo. La solución es clara: hay que aumentar el tiempo de muestreo cuando surgen fallos relacionados con la falta de tiempo o ciclos de sistema demasiado largos.