|
Wilson Dome, Pukekohe,
New Zealand
The Icosahedron
I was once a speaker at the N.Z.Institute of Building
Inspectors conference. I had the good fortune to follow two Forest Research
Institute wood scientists, whom had spoken for two hours about the moisture
content of timber framing.
I started by saying, " I'm going to tell you
about a four frequency oblate superellipsoidal icosahedron."
Someone yelled out, "Spell it!"
I retorted, "Clockwise or anti-clockwise?"
My audience was laughing and awake.
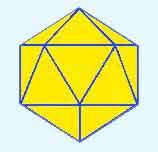
Consider a one frequency icosahedron (1v).
It consists of 20 equilateral triangles. It seems to be the most useful
polyhedron for dome building.Each vertex is the same distance from the
centre of this polyhedron and thus each vertex is on the surface of an
imaginary sphere. Note that one frequency is often written as 1v, two frequency
as 2v and so on.........
1v icosahedron (20 equilateral triangles)
 
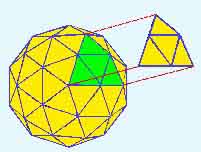
2v icosahedron
with 4 triangles per icosa face
Now take one of the original equilateral triangles.
It can be divided up into smaller triangles. Above is a 2 frequency (2v)
icosahedron. The icosa face (or basic triangle of the icosahedron) has
been broken up into four triangles. The side of the icosa face has been
divided into two, thus two frequency. Each vertex is on the surface of
an imaginary sphere. The higher the frequency, the more spherical the polyhedron
looks.
3 frequency (3v) with 9 triangles per icosa
face
 
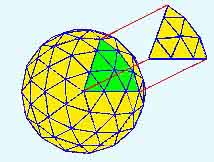
4 frequency (4v) with 16 triangles per icosa face.
And so on...
4v spheroidal icosahedron built
as a chapel for the Catholic Bishop of
the Waikato, NZ, the late Ed Gaines,
a true gentleman and friend.
Other Polyhedra
It is not just the icosahedron which can be used
to make a dome. Other polyhedra (such as the tetrahedron, the octahedron,
the dodecahedron and others) can be used. The same principles apply.
One frequency (1v) tetrahedron
 
One frequency (1v) Octahedron - half an octahedron is a pyramid.
Two frequency (2v) octahedron
 
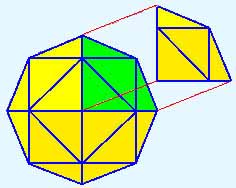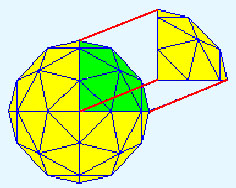
Three frequency (3v) octahedron
Other shapes and aspects
 It is
not only the sphere, which can be used as the shape of a dome. In all the
examples above, each vertex occurs on the surface of an imaginary sphere.
Each vertex could occur on the surface of an ellipsoid (squashed or stretched),
a super-spheroid, a super-ellipsoid or even a free form amorphous flow.
And the whole triangulated network (i.e. the dome) can be rotated to have
any point at the top, whether this is a vertex, the mid-point of an edge
or the centroid of a face.
 This
rotation can be done first, i.e. the spheroid is rotated and then squashed
or stretched, or the stretching or squashing can be done first and then
the ellipsoid ( or super-ellipsoid) can be rotated. For those really interested
in the mathematics, the best reference is "Geodesic
Math and How to Use It" by Prof. Hugh Kenner.
Please submit all questions and comments to geodesicsnz@oocities.com
|
