Curve Rodonia
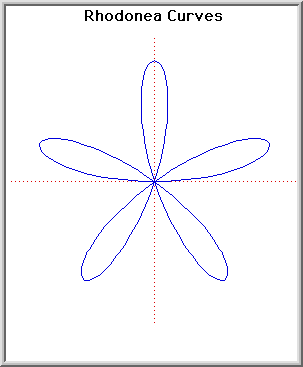
Equazione polare: r = a sin(k
)
Queste curve vennero cosi' chiamate dal matematico italiano Guido Grandi tra il 1723 ed il 1728, perche' somigliavano a rose.
Quando k e' un numero intero vi sono k oppure 2k petali a seconda se k e' dispari o pari. Se k e' irrazionale allora il numero di petali e' infinito.
Il quadrifoglio e' la curva rodonia con k = 2. Ha l'equazione polare r = a sin(2) e la forma cartesiana (x
+y) = 4axy.
Luigi Guido Grandi era un membro dell'ordine dei Camaldoliti. Divento' professore di filosofia nel 1700 e professore di matematica nel 1714, in entrambi le posizioni all'Universita' di Pisa.
Grandi fu anche l'autore di un certo numero di lavori sulla geometria in cui egli considero' le analogie tra il cerchio e l'iperbole equilatera. Egli considero' anche curve di doppia curvatura sulla sfera e la quadratura di parti di una superficie sferica.
[Nota del traduttore: Anche di questa curva esiste un giocattolo che permette di disegnare facilmente qualsiasi numero di petali, tra molte altre curve simmetriche.
Altri siti Web