Strega di Agnesi
Equazione cartesiana: y(x
+a) = a
oppure x = at, y = a/(1+t)
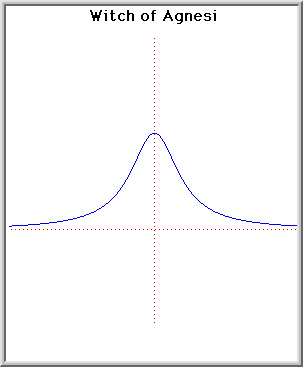
Questa curva fu studiata e chiamata 'versiera' (in cattiva traduzione la parola italiana fu tradotta "witch" che invece significa "strega") da Maria Agnesi nel 1748 nel suo libro Istituzioni Analitiche . E' anche nota come la 'Cubique d'Agnesi' oppure 'Agnésienne'.
La curva era stata studiata antecedentemente da Fermat e da Guido Grandi in 1703.
La curva sta tra y = 0 e y = a. Ha punti di inflessione a y = 3a/4. La linea y = 0 e' un asintoto alla curva.
Questa curva puo' essere considerata come il locus di un punto P definito come segue: Disegnamo un cerchio C con centro a (0,a/2) da O; disegnamo una linea che parta da O e tagli C a L e la linea y = a a M. Allora P ha la coordinata x di M e la coordinata y di L.
La tangente alla Strega di Agnesi al punto di parametro p e'
(p+1)y + 2px = a(3p+1).
Altri siti Web: