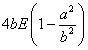
m EXE
K EXE E
(即是橢圓周界為 4 × 3 × 1.322119966 = 15.86543959)
Casio50 » fx-3x50P » Programs 程式集 » Special Functions 特殊函數 »
本式求 Complete Elliptic Integral of the First Kind K(m) 及 Second Kind E(m) 的值.
| <COMP> |
|---|
| ? → X : |
| 1 → A : √ ( 1 – X → B : √ X → C : |
| -1 → D : .5 X → M : |
| Lbl 0 : |
| .5 ( A – B → C : |
| √ ( A B → B : |
| A – C → A : |
| 1 + D → D : 2 ^ D C ² M+ : |
| ln e Ans => Goto 0 : |
| π ÷ 2 A → A ◢ |
| A – A M → B |
| 90 Bytes |
| 一般操作 | 例子 |
|---|---|
| 求 K(m) 和 E(m) 的值 | 求一個長短半軸分別為 2 和 3 的橢圓的周界. |
若一個橢圓的長短半軸分別為 a 和 b, 則其周界為 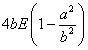 |
|
| 啟動程式 | 按 Prog 1 |
| 輸入資料 m EXE |
1 – 2² ÷ 3² EXE |
| 顯示答案 K EXE E |
1.904241417 EXE 1.322119966 (即是橢圓周界為 4 × 3 × 1.322119966 = 15.86543959) |
| A | K |
|---|---|
| B | E |
| C | c |
| D | iterations |
| X | m |
| Y | |
| M | s |
Complete Elliptic Integral of the First Kind 和 Second Kind 的定義分別為![]() 和
和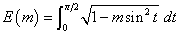 ,
其中 0 ≤ m ≤ 1.
,
其中 0 ≤ m ≤ 1.
本式不能正確地計算 m = 1 時的值. 這是因為 K(1) = ∞. 另外, E(1) = 1.
本式使用 Arithmetic-Geometric Mean 的方法求 E 和 K 的值.