ELECTRICITY AND MAGNETISM
Coulomb“s Law
|
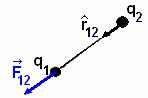
The force of attraction or repulsion between two point charges q1 and q2 is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. |
|
|
The unit vector
|
|
|
The constant
|
|
|
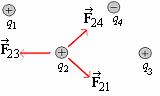
Coulomb“s law and the Principle of Superposition constitute the
physical input for electrostatics. The force on any one charge due to a
collection of other charges is the vector sum of the forces due to each
individual charge. Here F2=F21+F23+F24 |
|
|
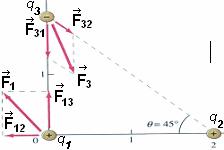
Problem Solving Strategies: 1. Draw a clear diagram of the situation. Be sure to distinguish between the fixed external charges and the charges which the forces must be found. The diagram should contain the coordinate axes for reference. 2. Electric force is a vector quantity; when many forces are present the net force is a vector sum. Example: Consider three point charges q1 = q2 = 2.0 mC and q3 = -3 mC which are placed as shown. Calculate the net force on q1 and q3. The force on q1 is F1 = F12 + F13. Similarly, F3 = F31 + F32 |
|
Electric Field
|
Electric field is defined as the electric force per unit charge. The direction of the field is taken to be the direction of the force it would exert on a positive test charge. The electric field is radially outward from a positive charge and radially in toward a negative point charge. The electric field can be defined by measuring the magnitude and direction of the electric force F on a test charge q0. A small test charge is used so as not to interfere with the field distribution of the other charges. Thus we define the electric field as |
|
|
The SI unit of electric field is NC-1. For a point charge |
|
Field Line Diagrams:
A convenient way to visualize the electric field due to any charge distribution is to draw a field line diagram. At any point the field line has the same direction as the electric field vector. Electric field lines diverge from positive charges and converge into negative charges.
Rules for constructing filed lines:
1. Field lines begin at positive charge and end at negative charge
2. The number of field lines shown diverging from or converging into a point is proportional to the magnitude of the charge.
3. Field lines are spherically symmetric near a point charge
4. If the system has a net charge, the field lines are spherically symmetric at great distances
5. Field lines never cross each other.
|
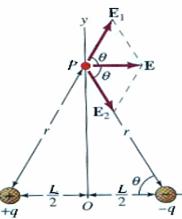
The Electric Dipole and their Electric Fields An electric dipole consists of two charges + q and ÷q, of equal magnitude but opposite sign, that are separated by a distance L. |
|
|
|
|
|
|
|
Define the product p = qL as the electric dipole moment. We make p = qL a vector by defining L to be directed from ÷q to +q. The vector p points from the negative charge to the positive charge. The electric field decreases with r as 1/r3. ŗFinally |
|
|
|
|
|
|
Charge Distributions:
The simplest kind of charge distribution is an isolated point charge (i.e., an amount of charge covering such a small region of space that we need not be concerned about its dimensions).
When the finite size of the space occupied by a collection of charges must be considered, it is useful to consider the density of charge. The word density is used is used in three different ways.
|
|
for the charge per unit volume, the volume density |
|
Cm-3 |
|
|
for the charge per unit area, the area density |
|
Cm-2 |
|
|
for the charge per unit length, the linear density |
|
Cm-1 |
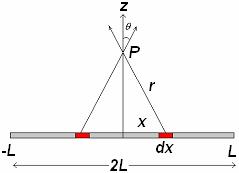
Find the electric field a distance z above the midpoint of a straight line segment of length 2L which carries a uniform line charge l.Thus we can write (Model of a transmission line)It is advantageous to chop the line up into symmetrically placed pairs (at - x). Here |
|
|
Here
|
|
How to evaluate this integral
|
|
|
Consider
|
Letŗ |
|
Substitute these into the integral: |
|
|
From
diagram, Hence
|
|
|
Substitute the limits x = 0 and x = L to get the desired answer. For points far from the line ( z >> L),
this result simplifies to .
|
|
|
The
line ”looks‘ like a point charge |
|
|
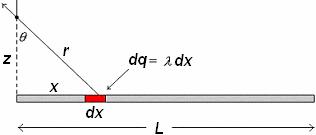
Find the electric field a distance z above one end of a straight line segment of length L, which carries a uniform line charge l.
|
(Model of a transmission line) ŗ |
|
Net electric field E = Ex + Ez
|
|
|
|
|
|
|
|
|
For
z >> L and |
|
|
Find the electric field a distance z above the center of a circular loop of radius R, which carries a uniform line charge l. Here,
Horizontal components cancel, leaving:
|
|
|
But
|
|
|
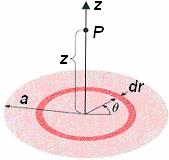
Find
the electric field a distance z above the center of a flat circular
disk of radius a, which carries a uniform surface density, A
typical element is a ring of radius r and thickness dr, which
has an area The
charge density on the disk is The charge on the element is:
|
(Models an electrostatic microphone)
|
|
The electric field at P produced by this ring is |
|
|
Since we have expressed a positive ring thickness as dr, we sum the rings from the center toward the edge. That is, the radius ranges from 0 to a.
|
|
|
Let
then du = 2r dr, and So
|
|
|
When z << a,
|
When
z >> a, |
|
Suppose that, instead of
having discrete charges, we have a continuous distribution of charge
represented by a charge density ρ(r). Thus, the charge at
position vector |
where the volume integral is over all space, or, at least, over all space for which ρ(r/) is non-zero |

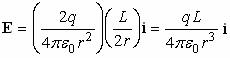


 , and x
runs from 0 to L
, and x
runs from 0 to L

 ;
;


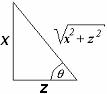













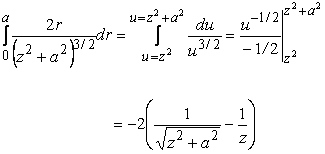

 ŗwhich is the
expected result for a point charge located at the origin.
ŗwhich is the
expected result for a point charge located at the origin.