Contoh Desain Sistem Kontrol Digital secara Klasik
Disadur dari contoh/demo control toolbox dari MatLab. Hak cipta (c) 1986-1999 pada The Mathworks, Inc. Penyadur: Husni Thamrin, ST

Plant: Head dari harddisk
Output: Posisi tulis/baca dari head
Input: Arus ke motor
Model sistem:

- dengan
- J = momen inersia dari head dan mekanik lainnya
- C = koefisien gesekan dari roda-roda gigi
- K = konstanta pegas
- Ki = konstanta torsional dari motor
- i = masukan arus ke motor
- q = posisi head
- dq/dt = kecepatan sudut head
- d2q/dt2 = percepatan sudut head
Transfer function: (diperoleh dengan mengambil transformasi Laplace dari model sistem di atas)

Misalkan nilai parameter sebuah sistem adalah:
J=.01 Kg m^2, C=.004 Nm/(rad/sed), K=10 Nm/rad, Ki=.05 Nm/rad
yang menghasilkan transfer function:
| 0.05 | |
| H(s) = | ----------------------- |
| 0.01 s2 + 0.004 s + 10 |
Target Kendali: Membuat kontroler digital yang dapat digunakan untuk memposisikan head dari harddisk secara akurat.
Proses Desain:
Untuk mendesain kontroler digital, transfer function diubah menjadi bentuk digital/diskret. Diskretisasi dilakukan dengan ZOH (zero order hold) dengan waktu sampling Ts = 0.005 (5 milidetik). Transfer function digital menjadi:
| 6.233e-005 z + 6.229e-005 | |
| H(z) = | ------------------------- |
| z2 - 1.973 z + 0.998 |
Bandingkan Bode plot sistem kontinyu dan diskret:

Bandingkan juga respon step sistem kontinyu dan diskret:
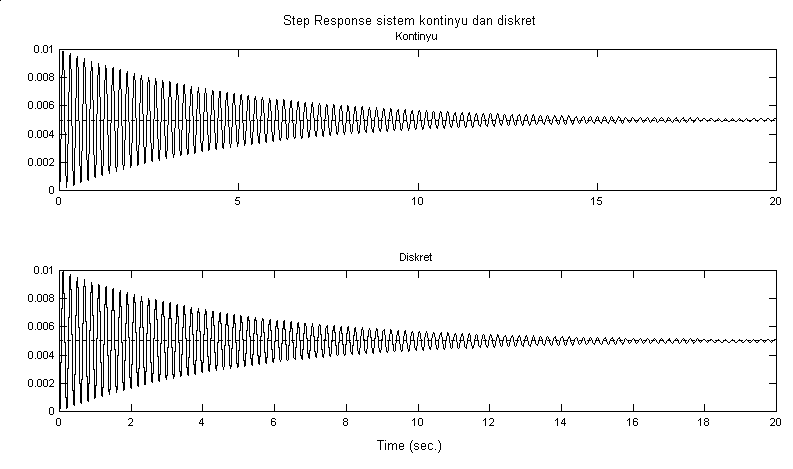
Sistem sangat berosilasi.
Pole zero plot dari sistem memperlihatkan letak pole yang dekat dengan lingkaran berjari-jari satu.
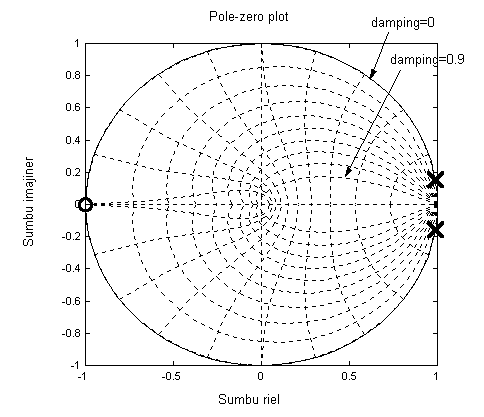
Desain sistem kendali dicoba dengan memberikan kompensator untuk meningkatkan peredaman (damping) dari sistem.
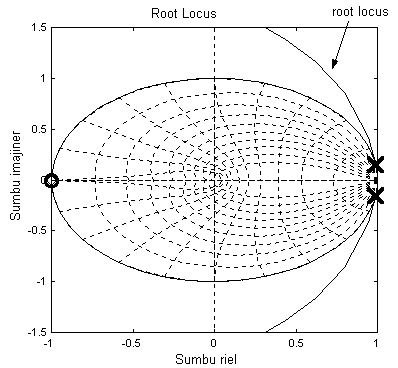
Root-locus memperlihatkan bahwa penambahan gain sistem kalang tertutup (closed-loop) cepat membuat pole sistem meninggalkan lingkaran berjari-jari satu sehingga menjadi tidak stabil. Kompensator yang ditambahkan bersifat lead, yaitu:
| z + a | |
| D(z) = | ----- dengan a < b |
| z + b |
Misalkan dicoba kompensator lead dengan nilai a = -.85 and b = 0.
Respon frekuensi akan berubah, pada grafik di bawah ini, respon frekuensi dari sistem yang belum dikompensasi adalah garis putus-putus. Tampak bahwa gain sistem pada frekuensi rendah telah meningkat.
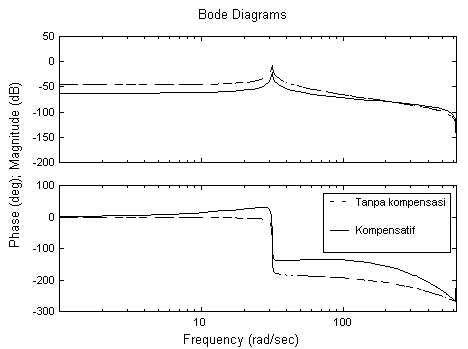
Sedangkan root locus sistem yang diberi kompensator adalah:
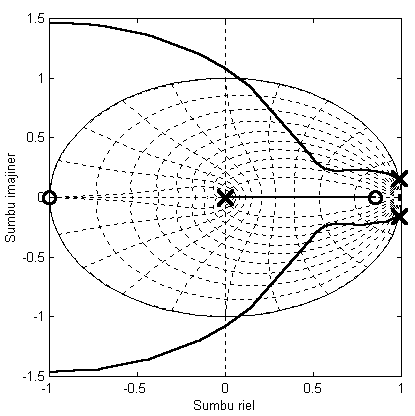
tampak bahwa sistem closed loop akan lebih stabil dibanding sistem tanpa kompensator. Pada gambar di atas, grid menunjukkan damping ratio dari 0 sampai 1 dengan step-step 0.1. Lingkaran terluar menunjukkan damping ratio 0 dan lingkaran terdalam menunjukkan damping ratio 1. Damping ratio 0 berarti sistem berosilasi murni (sinusoidal) tidak teredam sedangkan damping ratio 1 berarti sistem teredam kritis (=respon terbaik). Namun seperti tampak pada gambar, root locus tidak pernah melintas kurva dengan damping ratio 1 sehingga sebaik apapun, sistem tetap mengandung osilasi.
Dengan memilih gain sebesar 4150, akan diperoleh sistem dengan respon step seperti pada gambar di bawah ini.
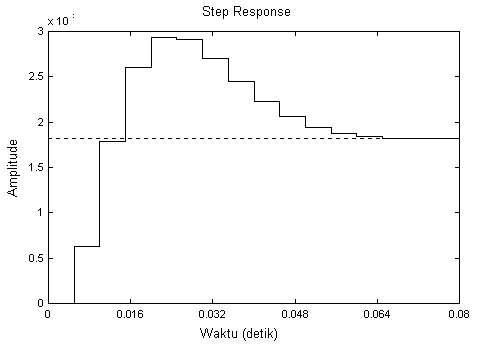
Respon tampak lebih baik dan mempunyai settling time sebesar 13 sample atau 13*0.005 = 0.065 detik. Dengan kontrol seperti ini, disk drive mempunyai seek time > 0.065 detik. (Masih terlalu besar untuk teknologi saat ini). Overshoot juga masih terlalu besar sampai 60 persen.
Kekokohan sistem kontrol secara klasik ditentukan dengan gain margin dan phase margin. Untuk itu dapat dilihat Bode plot:
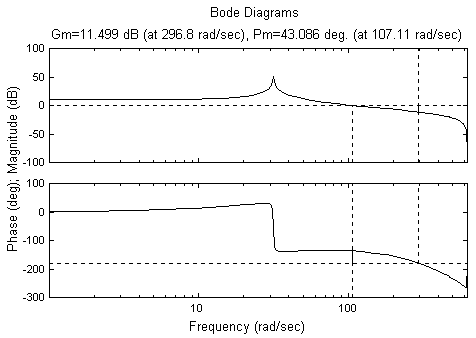
Dari Bode plot ini diperoleh gain margin = 11 dB dan phase margin = 43o. Hal ini menunjukkan sistem kontrol cukup kokoh karena dapat mentolerir kenaikan gain 10 dB dan lagging fase sebesar 40 derajat tanpa kehilangan kestabilan.
