Pole-Zero Plot dan Bode-Plot
Transfer function
Transfer function memberi gambaran lengkap tentang sebuah sistem linier. Jika transfer function suatu sistem diketahui, keluaran sistem terhadap berbagai bentuk masukan dapat dihitung, misalnya dengan metode transformasi. Jika transfer function diketahui, respon impuls dapat dihitung dengan invers transformasi. Dan jika respon impuls diketahui, respon sistem terhadap sembarang sinyal dapat dihitung dengan konvolusi. Oleh karena itu sistem linier sering digambarkan/dinyatakan dengan transfer function.
Patut diingat bahwa transfer function sistem linier kontinyu dinyatakan dalam bentuk transformasi Laplace dan transfer function sistem linier diskret dinyatakan dalam bentuk transformasi Z. Secara definitif, transfer function sistem kontinyu adalah perbandingan transformasi Laplace sinyal keluaran dan transformasi Laplace sinyal masukan, sedangkan transfer function sistem diskret adalah perbandingan transformasi Z sinyal keluaran dan transformasi Z sinyal masukan.
Transfer function sistem linier biasanya dinyatakan dalam bentuk fungsi rasional.
Fungsi rasional adalah fungsi yang merupakan rasio dua polinomial. Polinomial yang merupakan
pembilang disebut numerator dan polinomial yang merupakan penyebut disebut denominator.

Contoh 1. Fungsi rasional H(s)=1/(s+1) mempunyai gain K=1, numerator N(s)=1 dan denominator D(s)=s+1.
Contoh 2. Fungsi rasional H(z)=z/(z-0.7) mempunyai gain K=1, numerator N(z)=z dan denominator D(z)=z-0.7
Contoh 3. Fungsi rasional H(s)=5/s(s+2)=5/s2+2s mempunyai gain K=5,
numerator N(s)=1 dan denominator D(s)=s(s+2)=s2+2s.
Contoh 4. Fungsi rasional H(s)=(2s+1)/s2+2 mempunyai gain K=2,
numerator N(s)=s+0.5 dan denominator D(s)=s2+2.
Pole, Zero dan Pole-Zero Plot
Setiap polinomial P(x) mempunyai nilai nol. Nilai nol adalah suatu nilai x yang menyebabkan
polinomial P(x)=0.
contoh 1. Nilai nol polinomial P(x)=x+1 adalah x=-1 sebab jika nilai x=-1 dimasukkan ke
persamaan polinomial, maka P(-1)=-1+1=0.
contoh 2. Nilai nol polinomial P(x)=x2+x-2 adalah x=1 sebab jika nilai x=1
dimasukkan ke persamaan polinomial, maka P(1)=12+1-2=0. Nilai nol yang lain adalah
x=-2 sebab P(-2)=(-2)2-2-2=0.
contoh 3. Nilai nol polinomial P(x)=x2+2x+5 adalah x=-1+2j dan x=-1-2j sebab
P(-1+2j)=(-1+2j)2+2(-1+2j)+5=0 dan P(-1-2j)=(-1-2j)2+2(-1-2j)+5=0.
Perhatikan bahwa nilai nol bisa berupa bilangan kompleks.
Numerator dan denominator pada fungsi rasional juga mempunyai nilai nol. Nilai nol dari
numerator disebut ZERO dan nilai nol dari denominator disebut POLE. Pole dan zero merupakan
bilangan kompleks. Gambaran grafis pole dan zero tentulah pada bidang kompleks. Gambaran
grafis pole dan zero pada bidang kompleks disebut pole-zero plot.
Contoh 1. Sebuah sistem mempunyai transfer function H(s)=1/(s+1). Maka zeronya tidak ada,
dan polenya terletak di s=-1.
Contoh 2. Sistem diskret H(z)=z/(z-0.7) mempunyai zero di z=0 dan pole di z=0.7.
Contoh 3. Sistem H(s)=5/s(s+2) tidak mempunyai zero dan mempunyai pole di s=0 dan s=-2.
Contoh 4. Sistem H(s)=(s+2)/(s2+2s+5) mempunyai zero di s=-2 dan pole di
s=-1-j2 dan s=-1+j2.
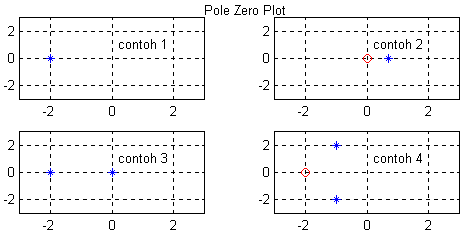
Pole zero plot dari keempat sistem pada contoh 1 sampai contoh 4 terlihat pada gambar ini.
Ingat keempatnya merupakan bidang kompleks, sumbu mendatar adalah bagian riel dan sumbu
vertikal adalah bagian imajiner.
Nilai nol polinomial dengan mudah dapat dihitung dengan MatLab. Perintah yang digunakan
adalah roots. Sebagai contoh untuk mencari nilai nol dari polinomial
s2+2s+5 maka dimasukkan perintah berikut:
POL=[1 2 5];roots(POL)
maka akan muncul jawaban
ans =
-1.0000 + 2.0000i
-1.0000 - 2.0000i
Perhatikan: untuk mencari nilai nol polinomial s3+4s, maka perintah yang dimasukkan
adalah
POL=[1 0 4 0];roots(POL)
Jika pole dan zero sebuah sistem diketahui, maka transfer function sistem dapat dihitung
asalkan gain sistem juga diketahui.
Contoh 1. Sistem dengan gain=2, zero tidak ada dan pole di s=-2 mempunyai numerator N(s)=1,
denominator D(s)=s+2 sehingga transfer functionnya adalah H(s)=2/(s+2)
Contoh 2. Sistem dengan gain=4, zero di s=-1, dan pole di s=-1+j dan s=-1-j mempunyai
numerator N(s)=s+1, denominator D(s)=(s+1-j)(s+1+j)=s2+2 sehingga transfer
functionnya adalah H(s)=4(s+1)/(s2+2)
Respon frekuensi
Respon frekuensi memberikan gambaran tentang cara sistem mengolah sinyal berfrekuensi.
Respon frekuensi dapat diperoleh dari transfer function dengan mengganti variabel s pada
transfer function dengan jw. Respon frekuensi tidak lain adalah
transformasi Fourier dari respon impuls. Bandingkan
tabel transformasi Fourier dengan tabel transformasi
Laplace. Tampak bahwa tabel transformasi Fourier dapat diperoleh dari tabel transformasi
Laplace dengan mengganti s dengan jw.
Contoh 1. Sistem H(s)=1/(s+1) mempunyai respon frekuensi
H(jw)=1/(jw+1)
Contoh 2. Sistem H(s)=(s+2)/(s2+2s+5) mempunyai respon frekuensi
H(jw)
=(jw+2)/((jw)2+2jw+5).
Bode Plot
Respon frekuensi merupakan fungsi kompleks. Fungsi seperti ini dapat dinyatakan secara
secara kartesian dengan penjumlahan fungsi riel dan fungsi imajiner. Atau dapat pula
secara polar dengan fungsi magnitudo dan fungsi sudut/fase.
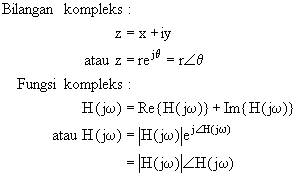
Contoh:
Contoh. Jika sistem H(s)=1/(s+1) diberi masukan x(t)=sin 50t bagaimana keluarannya?
Jawab. Sinyal masukan adalah sinyal berfrekuensi dengan amplitudo 1 dan frekuensi 50 rad/s
dan fase=0 radian. Respon frekuensi sistem adalah H(jw)
=1/(jw+1) sehingga untuk frekuensi w=50
diperoleh H(j50)=1/(j50+1). Dari sini diperoleh magnitudo=|H(j50)|= 0.0995 dan
fase=ÐH(j50)=arctan(1/50)=0.02 radian=1.15°.
Maka keluaran adalah y(t)=0.0995 sin(50t+0.02).
Respon frekuensi dapat digambarkan secara grafis. Untuk menyatakan respon frekuensi secara
grafis diperlukan dua grafik. Yang satu adalah grafik magnitudo terhadap frekuensi dan yang
lain adalah grafik fase terhadap frekuensi. Umumnya, sumbu frekuensi digambarkan secara
logaritmis. Sedangkan magnitudo dinyatakan dalam dB (desiBell) di mana (X dalam dB)=(20 log X).
Bentuk seperti yang terakhir ini disebut Bode plot. Di bawah ini adalah gambar Bode plot untuk
sistem H(s)=1/(s+1) seperti yang digambar oleh MatLab. 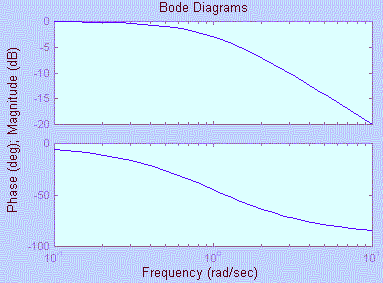
Respon sistem terhadap masukan berfrekuensi dapat diperkirakan dengan melihat grafik.
Perhatikan bahwa sumbu mendatar adalah sumbu frekuensi dengan skala logaritmis. Titik paling
kiri dari sumbu mendatar adalah frekuensi w=10-1=0.1.
Tepat di tengah sumbu mendatar adalah frekuensi w=100=1.
Dan titik paling kanan sumbu mendatar adalah frekuensi w
=101 =10. Inilah yang dimaksud skala logaritmis.
Sumbu vertikal grafik fase adalah sudut dalam derajat (bukan radian) seperti yang biasa
dipakai orang. Sumbu vertikal grafik magnitudo adalah dalam dB. Perlu diketahui bahwa untuk
rangkaian penguat elektronik magnitudo sistem disebut juga gain (atau penguatan).
Jika Bode plot sistem tersedia, respon sistem terhadap masukan berfrekuensi dapat dihitung
secara grafis (tentunya ketelitiannya rendah). Nilai magnitudo dan fase yang ditunjukkan oleh
grafik adalah perubahan yang dilakukan oleh sistem terhadap magnitudo dan fase sinyal.
Contoh 1. Jika sinyal x(t)=2 sin(5t+50°) dimasukkan ke sistem dengan bode plot
seperti tergambar di atas, bagaimana sinyal keluarannya?
Jawab: sinyal masukan mempunyai magnitudo = 2, fase=50°, dan frekuensi=5 radian/detik.
Dari Bode plot dapat dilihat bahwa untuk frekuensi 5 rad/det respon sistem untuk magnitudo
adalah sekitar -14dB dan respon sistem untuk fase sekitar -80°. Magnitudo -14dB setara
dengan magnitudo sebesar
10-14/20=10-0.7=0.1995.
Maka sinyal keluaran mempunyai magnitudo 2*0.1995=0.399 dan fase 50°-80°=-30°
Jadi sinyal keluaran adalah y(t)=0.399sin(5t-30°).
Contoh 2. Sinyal x(t)=10 cos (t+20°) dimasukkan ke sistem dengan Bode plot
seperti di atas. Tentukan sinyal keluarannya.
Jawab:
Masukan: magnitudo=10, fase =20°, frekuensi =1 rad/det.
Respon untuk frek. 1 rad/det: fase=-45°, magnitudo=-3dB=10-3/20=10-0.15 =0.7
Keluaran: magnitudo=10*0.7=7, fase=20°-45°=-25° Jadi sinyal keluaran adalah
y(t)=7cos(t-25°).
Latihan 6.
Topiknya adalah pole-zero plot dan bode plot dan antara lain menggunakan MatLab. Program MatLab dapat dipelajari. Perhatikan bahwa grafik pada MatLab dapat di-zoom jika diperlukan. Pada soal-soal ini, a=tiga digit terakhir NIM, dan b=digit terakhir NIM.
Soal 1. Sebuah sistem mempunyai respon impuls h(t)=be-atu(t). Tentukan transfer function sistem. Tentukan numerator dan denominator. Dan tentukan pole dan zeronya.
Soal 2. Untuk sistem berikut ini: H(z)=[1-2z-1+az-2]/[1-4z-b] tentukan numerator dan denominator dan tentukan pole dan zeronya.
Soal 3. Untuk sistem dengan respon impuls seperti pada soal 1, tentukan respon frekuensi.
Soal 4. Untuk sistem yang mempunyai gain=2, zero di s=0, dan pole di s=-b+ja dan s=-b-ja, tentukan numerator, denominator dan transfer function.
Soal 5. Untuk sistem dengan respon frekuensi seperti pada soal 3, jika diberi masukan sinyal x(t)=b sin (100at), tentukan keluarannya.
Soal 6. Dengan MatLab gambarlah pole-zero plot dari sistem seperti pada soal 2.
Soal 7. Dengan MatLab gambarlah Bode plot dari sistem dengan transfer function:
H(s)=a/(s2+s+b).
Soal 8. Dari gambar Bode plot pada soal 7 tentukan gain sistem untuk frekuensi a rad/det.
