Realisasi Sistem Linier
Yang dimaksud dengan realisasi sistem adalah penggambaran sistem ke bentuk diagram blok yang terdiri atas unsur-unsur elementer penyusun blok. Realisasi mutlak diperlukan ketika akan mewujudkan sistem linier diskret baik dengan perangkat lunak atau dengan perangkat keras. Realisasi juga dibutuhkan ketika akan mensimulasi sistem linier kontinyu dengan perangkat lunak. Sedangkan pewujudan sistem linier kontinyu ke perangkat keras lebih sering dilakukan secara langsung dari transfer function sistem orde satu dan sistem orde dua, tanpa melalui realisasi.
Komponen-komponen realisasi
Realisasi biasanya berangkat dari bentuk transfer function sistem. Jadi transfer function
sistem harus diketahui terlebih dahulu. Tapi dapat pula realisasi berangkat dari persamaan
diferensial sistem kontinyu (differential equation) atau persamaan bedaan sistem diskret (difference equation).
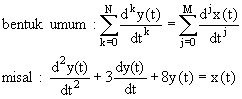
- Jika diperhatikan persamaan diferensial sistem linier kontinyu, maka ada tiga operasi
matematis yang muncul:
- Penjumlahan
- Perkalian dengan konstanta
- Pendiferensialan
- Dan jika diamati persamaan bedaan sistem linier diskret, maka ada tiga operasi
matematis yang muncul:
- Penjumlahan
- Perkalian dengan konstanta
- Tundaan (delay)
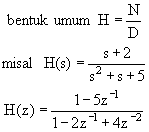
- Sedangkan pada transfer function sistem terdapat tiga operasi
matematis yang muncul:
- Penjumlahan
- Perkalian dengan konstanta
- Perpangkatan variabel s pada sistem kontinyu atau variabel z pada sistem diskret
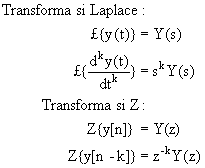Namun operasi perpangkatan variabel z pada bentuk transfer function setara dengan proses
tundaan pada persamaan bedaan sistem diskret. Dan operasi perpangkatan variabel s setara
dengan operasi pendiferensialan pada sistem kontinyu. Jika transformasi Laplace dari sinyal
y(t) adalah Y(s), maka transformasi Laplace dari dy(t)/dt adalah sY(s) dan transformasi
Laplace dari dmy(t)/dtm adalah
smY(s). Jika transformasi Z dari y[n] adala Y(z) maka transformasi Z dari y[n-1]
adalah z -1Y(z) dan transformasi Z dari y[n-k]
adalah z -kY(z).
- Kini jelaslah bahwa diperlukan tiga macam komponen untuk merealisasikan sistem linier,
yaitu
- Penjumlah: untuk merealisasikan proses penjumlahan, untuk sistem kontinyu dan diskret.
- Pengali=Penguat=Gain: untuk merealisasikan proses perkalian dengan konstanta, untuk sistem kontinyu dan diskret.
- Tundaan: untuk merealisasikan proses tundaan, untuk sistem diskret
atau Differensiator/derivatif: untuk merealisasikan proses pendiferensialan, untuk sistem kontinyu
atau Integrator: untuk merealisasikan proses integral yang merupakan kebalikan proses pendiferensialan, untuk sistem kontinyu.
| Komponen dan Bentuk | Sinyal Masukan | Sinyal Keluaran |
Penjumlah: |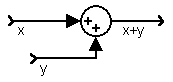
x(t), y(t) | x(t)+y(t) |
| X(s), Y(s) | X(s)+Y(s) | |
| x[n], y[n] | x[n]+y[n] | |
| X(z), Y(z) | X(z)+Y(z) | |
Pengali: |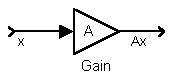
x(t) | Ax(t) |
| X(s) | AX(s) | |
| x[n] | Ax[n] | |
| X(z) | AX(z) | |
Diferensiator=Derivatif: |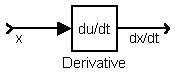
x(t) | dx/dt |
| X(s) | sX(s) | |
Integrator: |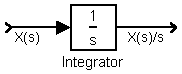
x(t) |  |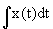
| X(s) | X(s) s | |
Tundaan=Delay: |
x[n] | x[n-1] |
| X(z) | z -1X(z) = X(z)/z |
Realisasi Langsung Bentuk I
Ada beberapa konfigurasi dalam realisasi yaitu realisasi langsung, realisasi paralel, realisasi kaskada, realisasi ladder, dan lain-lain. Di sini hanya akan dikenalkan mengenai Realisasi Langsung melalui contoh-contoh. Contoh-contoh berikut ini mengenai realisasi sistem diskret.
Contoh 1. Realisasikan sistem ini: y[n]=2x[n-1]
Jawab: Masukan sistem adalah x[n] dan keluarannya adalah y[n]. Setelah melewati pengali
gain=2 maka sinyal x[n] berubah menjadi sinyal 2x[n]. Dan setelah melewati tundaan, sinyal 2x[n]
berubah menjadi sinyal 2x[n-1].
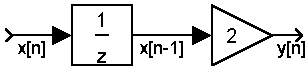
Contoh 2. Realisasikan sistem ini: y[n]=3x[n]-x[n-1]
Jawab: Sinyal masukan dialirkan ke dua komponen. Satu menuju pengali dengan gain=3 dan satu
lagi menuju pengali dengan gain=-1 dan tundaan. Setelah itu kedua sinyal dijumlahkan dan
menghasilkan sinyal 3x[n]-x[n-1].
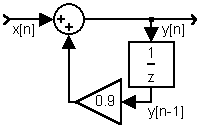
Contoh 3. Realisasikan sistem ini: y[n]-0.9y[n-1]=x[n]
Jawab: Persamaan sistem di atas setara dengan persamaan y[n]=0.9y[n-1]+x[n]
Contoh 4. Realisasikan sistem ini: y[n]-0.6y[n-1]+0.5y[n-2]=x[n-1]
Jawab: Persamaan sistem di atas setara dengan persamaan y[n]=0.6y[n-1]-0.5y[n-2]+x[n-1]
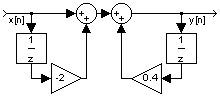
Contoh 5. Realisasikan sistem ini: y[n]-0.4y[n-1]=x[n]-2x[n-1]
Jawab: Persamaan sistem di atas setara dengan persamaan y[n]=0.4y[n-1]+x[n]-2x[n-1]
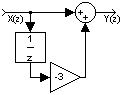
Contoh 6. Realisasikan sistem ini: Y(z)=X(z)-3z -1X(z)
Jawab:
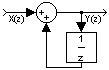
Contoh 7. Realisasikan sistem ini: H(z)=1/(1-z -1)
Jawab: H(z) adalah transfer function yang sama dengan Y(z)/X(z). Jadi persamaan di atas
dapat diubah menjadi
Y(z)/X(z)=1/(1-z -1)
Y(z)(1-z -1)=X(z)
Y(z)-z -1Y(z)=X(z)
Y(z)=z -1Y(z)+X(z) dengan realisasi:
Contoh 8. Realisasikan sistem ini: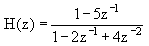
Jawab: Persamaan di atas dapat diubah menjadi:
dengan realisasi:
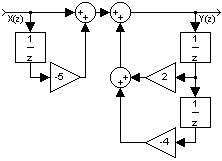
Contoh 9. Realisasikan sistem ini: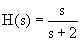
Jawab: Persamaan di atas dapat diubah menjadi:
dengan realisasi:
Contoh 10. Realisasikan sistem pada soal 9 dengan menggunakan komponen Integrator:
Jawab: Agar dapat direalisasikan dengan komponen integrator, diusahakan agar numerator dan
denominator bukan merupakan perpangkatan s melainkan perpangkatan s-1. Karena itu
numerator dan denominator pada persamaan di atas masing-masing dibagi dengan s sehingga
diperoleh persamaan
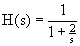yang dapat diubah menjadi:
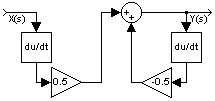
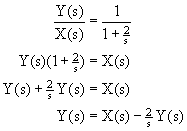dengan realisasi:
Contoh 11. Realisasikan sistem ini dengan komponen integrator: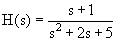
Jawab: Dengan membagi numerator dan denominator dengan s2, persamaan di atas
berubah menjadi:
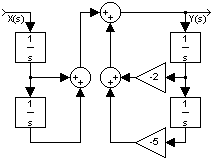
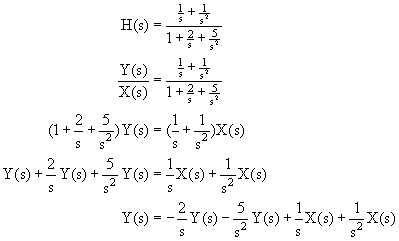dengan realisasi:
Realisasi Langsung Bentuk II
Realisasi Langsung Bentuk II merupakan modifikasi dari realisasi langsung bentuk I dengan
keuntungan berupa jumlah tundaan/integrator yang minimal. Perhatikan realisasi sistem
pada contoh 5 di atas yang digambarkan lagi di bawah ini.
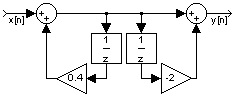
Realisasi sistem di atas menggunakan dua buah komponen tundaan. Berdasarkan sifat asosiatif
sistem linier, realisasi di atas dapat diubah menjadi bentuk seperti di bawah ini.
Pada gambar terakhir ini, terlihat bahwa kedua komponen tundaan itu mempunyai sinyal
masukan yang sama. Karena itu cukup digunakan satu komponen tundaan seperti
gambar di bawah ini:
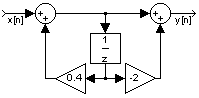
Bentuk seperti inilah yang dimaksud dengan realisasi langsung bentuk II yang secara umum
lebih baik dari realisasi langsung bentuk I.
Latihan 7.
Topiknya adalah realisasi sistem linier, dan simulasi sistem dengan MatLab/Simulink. Simulink adalah salah satu TOOLBOX dari MatLab. Jika MatLab diinstal lengkap, maka salah satu komponennya adalah Simulink. Tentang MatLab/Simulink dapat dipelajari. Ingat a=tiga digit terakhir NIM, b=digit terakhir NIM.
Soal 1. Realisasikan sistem berikut ini: y[n]= ax[n-1]
Soal 2. Gunakan Realisasi Langsung Bentuk II untuk merealisasi sistem y[n]-y[n-b]=x[n]-0.5x[n-1]
Soal 3. Realisasikan sistem ini dengan integrator H(s)=(s+a)/(sb+2)
Soal 4. Sebuah sistem diskret mempunyai gain K=2, zero di z=b/10 dan di z=a/200 dan pole di z=b/a dan di z=0.6, tentukan transfer functionnya dan realisasikan sistem dengan realisasi langsung bentuk II.
Soal 5. Hitunglah transfer function sistem invers dari sistem pada soal 4. Beri nama HI(z).
Soal 6. Realisasikan HI(z) dari soal 5 dengan realisasi langsung bentuk II.
Soal 7. Buatlah model simulink dari H(z) dan HI(z) dalam bentuk seperti gambar di bawah ini
Gunakan komponen Step sebagai sumber sinyal. Gunakan Sample time=0.1 detik. Jalankan simulasi. Dan print bentuk sinyal yang dikeluarkan oleh osiloskop.
Soal 8. Ulangi soal 7 untuk sumber sinyal Sinusoidal dengan amplitudo=1 dan frekuensi 1 hertz. Jangan lupa untuk menyetel Sample time=0.1 detik.