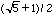Solution

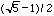
Assume the serie of numbers is: s₀, s₁, s₂, s₃, ... = 1, 1, 2, 3, ...
It is easy to see that : s_n = s_n-1 + s_n-2
 

The next numbers in the serie : 1,1,2,3,5,8,13,21,34, ... are thus : 55, 89, 144, ...

In what way is the serie related to square root of  5?

To examine this let us assume the solution has the form

s_n = A rⁿ

for a arbitrary member in the serie. The assumptions need not necessary be right - that depends of the possibility to determin  A and r. If the assumption is right then

A rⁿ = A r^n-1 + A r^n-2 or after dividing by  A r^n-2

 r² = r + 1

 i.e. two solutions are possible that is
 
 

r = r1 = 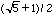 och r = r2 =

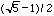Both solutions are thus related to the square root of 5! The n:th term in the serie is a combination of the solutions:

 s_n = A r₁ⁿ + B r₂ⁿ

A and  B can be determined from for instance the two first terms  s₀ and s₁

Compute square root of 5 with 3 decimals using the serie!

For large values of n the terms are dominated by the contribution from  r₁, i.e.

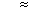s_n A r₁ⁿ
 
 

The quota kn = sn/sn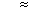-1r1

and thus since  r₁ = 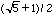  we can write
 

2*sn/sn-1 -1

 

n	5	6	7	8	9	10	11	12	13
sn	8	13	21	34	55	89	144	233	377
2*sn/sn-1 -1	--	2,25	2,2308	2,2381	2,2353	2,23636	2,235955	2,23611	2,2360515

For instance 2*89/55 - 1 = 2.23636 ... that is correct to 3 decimals when compared to the correct value 2.23606 ...

More

Back to weekly quiz