
Three students were about to get their caps from the President of the school. They were seated in the auditorium in such a way that only the student furthest back could see the both the others. The student in the middle could only see the student in front of him ( that student was blind, unfortunately for himself).
The President had 5 caps, 3 white and 2 black. This
was well known to all. He started with putting a cap on the head of the
student sitting behind the others and continued forward to the student
in the first row ( the blind one). Nobody was able to see either his own
cap or the remaining caps.
Then the President asked the student if they knew the
color of their own cap.
After a while the blind student said that he knew. What color did he had? How could he know?
Solution
Problem 2: Cows
A farmer had three equal meadows where his cattle could eat. At one occasion he let loose 7 cows on one meadow, 3 cows on the second and 1 cow on the last. He observed that the first meadow was eaten after 3 days and the second after 8 days. How long did it take until the last meadow was eaten?
Problem 3: Shakespearean English
What is the output signal y from the OR circuit below?

Please continue the number series starting with: 1,1,2,3,5,8,13,21,34, ...
In what way is this related to the square root of
5?
Compute the square root of 5 with 3 decimals using
the series!
A man with 3 sons had 17 camels. He worried of how the sons (daughters are not mentioned) could inherit. According to the law in his country the first born was to inherit half of his fortune, son nr 2 should have a third and son nr 3 a ninth. But as 17 was a prime and the camels could not be divided.
"Don't worry" his old friend said. You can borrow one camel from me. Then you have 18 and your sons can get 9, 6 and 2 camels each; all according to the law. Then you give me back the resting camel, that you borrowed from me, and nobody will be discontent!
"You are really a friend I can rely on in my difficult hours" the once so worried man answered, "Your solution is a wonder, but it is correct and I will act according to it".
Now I ask you was it a wonder or what is the explanation?
-"Like to play quad?" Jim asked his friend Jack. -"What
is that ?" Jack said. Jack was not as experienced in these games that were
dominating the campus.
-"Well", said Jim, -"let us do this. You throw a coin
until the mark comes up. When it does, I will pay you as many dollars as
the square of the number of throws you needed. You pay me a fixed fee of
say 5 dollars for each game!"
-"With pleasure!" Jack answered. He had grasped
the possibility to earn some easy money. But was he right?
What should the fee for each game be if it was to be
fair?
Hint: You may need to know that ![]()
In a tournament of tennis there are 111 players. Some of the participants are seeded and do not participate in the first rounds of matches. How many matches must be played before the winner can get his prize?
Problem 8: Context
This is a real classic. It is contained in many intelligence
test. The problem is to unite all the points in the figure with 4 straight
lines in such a way that all points are passed by exactly one line. The
pen mustn't be lifted while drawing!

Once when I was serving for
my practice as an engineer I was working at a building. One day the foreman
came and said: - " We need to put this 10m long ladder up along the wall
right at the place where there is a tank formed as a cube with 1m side
standing at the wall." - "My problem is that I cannot figure out
how far it will reach. But you, who is to become an engineer can perhaps
help me there? I need to know it with 3 decimals precision."
- "No problem Mr. foreman"
I said, "you will have the solution in 10 min!"
How far up does the ladder
reach?
-"This
year the added ages of my three daughters equals the street number in my
address." Sean told Brian.
-"
Can you tell their ages?"
-"
No!!! You must know this is impossible from what you just have told
me!" replied Brian, who knew the street number but could not figure out
the ages.
-" I
can hint you that the product of their ages is 72 " Sean said.
-" Oh,
I guess I need something more if you expect me to be able to tell !"
-" Then,
if I tell you that the oldest has a wonderful voice and can sing?" Sean
added.
-" Thank
you! That was what I needed " Brian said and looked content.
How old
were the daughters?
Hint: You may need some help to survey all numbers whose product is 72. This is given in the following MatLab program (Solving by hand may be quicker if you aren't familiar with MatLab!).
How can you fill exactly 4 liters of water on a bottle that contains 5 liters if you also have a 3 liter bottle? There is no need to save water!
A traffic beacon shows red for 30 seconds and green also for 30 seconds. There is no yellow light between. How long on average do you have to wait at the beacon?
Four stock cars were parked in the edges of a square with the side length of 1 km. Simultaneously they started to drive clockwise towards next car as shown in the figure below. The car had all the same performances , accelerated equally fast etc. Each drove shortest way straight towards next car in the spiraling orbit shown. How many kilometers did it take for each of the car until at last they all collided in the center of the square?
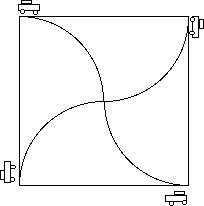
In a house far away there lived three men. One of them always told the truth, another always lied and the third sometimes told the truth sometimes told a lie. They were well aquatinted since many years back. How can you by asking just three questions to one of them at a time be sure of who is who amongst them?
Problem 15: Three women in a boat
Two brothers stand looking at a lake. Out there is a rowing boat with 4 persons onboard. Three women and a vicar.
-"How old are the women if the product of their ages is 2450?" says one brother to the other.
-"I cannot tell you from that, you have to tell me more".
-" Of course. You know how old dad is. He isn't in the boat but his age is equal to the the sum of all three womens ages."
-"I still cannot say. Tell me more!"
-"OK. Let me then say that the vicar is the oldest in the boat. Now you ought to know!"
-" Of Course! The women must be ..."
Here we leave the brothers, but the ages he now concluded were the right ones. The information given is sufficient to get the ages of the women and the dad.
I make it somewhat more difficult for you. I want to know:
HOW OLD IS THE VICAR?
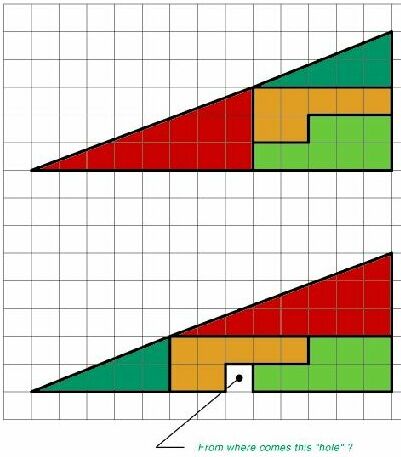
The areas above consists of exactly the same parts, all colored in different colors. Still there is something wrong because the areas are not equal. What is wrong?
Three students sat at a table. They all had a can
of beer.
" I bet that my can will roll down that tilting table
faster than yours" said Brian who was a notorious gambler and still hadn't
opened his can. He continued: The cans must all start at zero speed at
the higher end of the table. You can empty your can or fill it with anything
you want but the can must be unchanged in its exterior.
-" I am on" said Eric, who already had emptied his can
and was thinking it would roll easier without its heavy content.
-" Count on me" Sean said. He was thinking to fill his
can with sand and thus make it heavy and overcome the air resistance much
easier and thus win the race.
Now I ask you dear reader
a. Who won?
b. Who's can was slowest?
c. Why?