The goal of MasterMind is to figure out a hidden code in as
few guesses as you can. The code consists of a row of coloured
pegs hidden behind a screen.
You use the hand to pick up coloured pegs and place them in the guess row. When you're satisfied with your guess, press the OK
button. MasterMind then compares your guess with the hidden code,
and puts black and/or white pegs in the clue column telling
you how close your guess was. To begin playing, the only thing
you have to understand is what the black and white clue pegs mean.
What the black and white clue pegs mean
A black peg means that one of the pegs in your guess is the same colour in the same position as a peg in the code. A white peg means that one of the pegs in your guess has the same colour as a peg in the code, but your peg is not in the same position. There are two important things to keep clear about the clue pegs. First, the positions of the black and white clue pegs have nothing to do with the pegs in your guess. Second, each clue peg compares exactly one peg in your guess with exactly one peg in the secret code, and clue pegs never refer to more than one peg in the guess or more than one peg in the secret code; so, two white pegs never mean that one of the pegs in your guess is the same colour as two pegs in different positions in the code. This rule is trickier to explain than it is to follow. (Another way to put it is that there is a 1:1:1 ratio between guess:clue:code pegs. There! Much clearer.) Here are two examples illustrating the clue pegs.
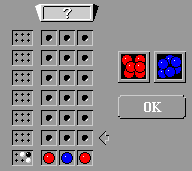In Example 1 (left), the black peg tells us that one of the coloured
pegs in the guess is in the right position, but it doesn't tell
us which one. The two white pegs mean that there are two pegs
in the guess which are the right colour but in the wrong position.
The fact that there are as many clue pegs as pegs in our guess
tells us that each of the pegs in the guess appears in the code
(i.e. there are two Red and one Blue in the code). Can you use
the clue in row 1 to figure out what the code might be? (Hint:
there are two codes consistent with this guess and clue.)
Compare Example 1 (above) with Example 2 (left). It seems we haven't been as lucky in our
first guess: this time we got only two clue pegs, and no black
pegs. However, we can deduce a lot from those two white pegs.
First, because there are only three pegs in the guess (red, red,
blue) we know that (at least) one of the white pegs must be telling
us about a red peg in our guess: it tells us that there is a red
peg in the code, but not in the same position as in our guess.
This means that there must be a red peg in the third column
(where the blue peg is in the guess in row 1). We also know that
the second white clue peg must be referring to the blue peg in
our guess: telling us that a blue peg appears in the code, but
not in column 3. (There is more than one way to deduce this, the
most important following from the second point mentioned above:
that if both white clue pegs referred to red pegs, they would
be telling us that they both belonged in the column 3 hole, but
different clue pegs never refer to the same code peg.) From this we
can figure out exactly what the secret code must be. Can you?
Introducing... |
Playing... |
Playing Better... |
Download... MasterMind
Copyright © 1998-2002 John Upper
