Soluzioni delle equazioni xn=1

Nota: Le soluzioni delle equazioni xn=1 vengono anche chiamate radici n-esime dell' unità.
Quando calcoliamo 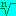a, in realtà cerchiamo il numero x tale che xn=a. Un operazione per convenzione dà un solo risultato, ma chi ci assicura che x sia unico? In effetti non lo è. E allora come lo scegliamo? Tra numeri non reali e numeri reali scegliamo quelli reali, tra numeri negativi e positivi scegliamo quello positivo. Si può dimostrare che con queste scelte, se a è un numero reale, ci rimane un solo numero.
Esempio:
Vogliamo sapere quanto fa 9: i numeri x tali che x2=9 sono 3 e -3 perché 32=9 e (-3)2=9. Per convenzione poniamo 9=3.
Generalizziamo: vogliamo calcolare 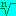a (prendiamo n come numero naturale). Per prima cosa dobbiamo trovare tutti i numeri x tali che xn=a. Una volta fatto, scegliamo quello che ci interessa (questo è un ragionamento teorico: praticamente si trova il risultato colla calcolatrice o a mente). È importante osservare che questi numeri x sono tutti e soli le soluzioni dell' equazione polinomiale xn=a o di quella equivalente xn-a=0.
Nota: Se n è un numero naturale ed a un numero reale, le soluzioni rappresentate nel piano complesso sono i vertici di un poligono regolare avente n lati.
Nel caso delle equazioni di secondo grado, che sappiamo avere 2 soluzioni, nella formula risolutiva c' è una radice quadrata preceduta da ±. Così otteniamo 2 soluzioni: una considerando il valore della radice quadrata, l' altro considerando il suo opposto. Questo vale perché un numero ed il suo opposto elevati al quadrato danno lo stesso numero e non c' è nessun altro numero che elevato al quadrato dia quel numero.
Ma in generale, conoscendo il valore di 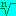a, come si fa a trovare tutti gli altri numeri x tali che xn=a?
Per prima cosa risolviamo il problema più semplice di calcolare tutte le soluzioni di xn=1 (poi vedremo che da questo si potrà dedurre il caso in cui al posto di 1 c' è a). È quello che faremo in questa pagina.
Dal teorema fondamentale dell' algebra sappiamo che xn=1 ha esattamente n soluzioni tra i numeri complessi.

Metodo generale per trovare le soluzioni di xn=z con z complesso

 Per riuscire a capire quanto segue dovete conoscere i numeri complessi e la trigonometria.

Innanzitutto bisogna sapere che |a+b*i|*|c+d*i|=|(a+b*i)*(c+d*i)|.
|a+b*i|*|c+d*i|=
(a2+b2)*(c2+d2)=
((a2+b2)*(c2+d2))=
(a2*c2+a2*d2+b2*c2+b2*d2)

|(a+b*i)*(c+d*i)|=
|a*c+a*d*i+b*i*c+b*i*d*i|=
|a*c+b*d*i2+(a*d+b*c)*i|=
|a*c+(b*d)*(-1)+(a*d+b*c)*i|=
|a*c+(-b*d)+(a*d+b*c)*i|=
|a*c-b*d+(a*d+b*c)*i|=
((a*c-b*d)2+(a*d+b*c)2)=
((a*c+(-b*d))2+(a*d+b*c)2)=
((a*c)2+2*(a*c)*(-b*d)+(-b*d)2+(a*d)2+2*(a*d)*(b*c)+(b*c)2)=
(a2*c2+b2*d2+a2*d2+b2*c2+2*a*b*c*d+(-1)*2*a*b*c*d)=
(a2*c2+a2*d2+b2*c2+b2*d2+2*a*b*c*d+(-2*a*b*c*d))=
(a2*c2+a2*d2+b2*c2+b2*d2+2*a*b*c*d-2*a*b*c*d)=
(a2*c2+a2*d2+b2*c2+b2*d2+0)=
(a2*c2+a2*d2+b2*c2+b2*d2)
Dalla proprietà sopra segue che (basta ripetere la moltiplicazione con termini tutti uguali)
(|a+b*i|)n=|(a+b*i)n|
Considero i numeri complessi a+b*i il cui angolo associato è p e c+d*i il cui angolo associato è q. Come abbiamo visto allora
a+b*i=|a+b*i|*(cos p+sen p*i)
c+d*i=|c+d*i|*(cos q+sen q*i)

Bisogna sapere che
|a+b*i|*(cos p+sen p*i)*|c+d*i|*(cos q+sen q*i)=|(a+b*i)*(c+d*i)|*(cos (p+q)+sen (p+q)*i)
 |a+b*i|*(cos p+sen p*i)*|c+d*i|*(cos q+sen q*i)=
|(a+b*i)*(c+d*i)|*(cos p*cos q+cos p*sen q*i+sen p*i*cos q+sen p*i*sen q*i)=
|(a+b*i)*(c+d*i)|*(cos p*cos q+sen p*sen q*i2+(cos p*sen q+sen p*cos q)*i)=
|(a+b*i)*(c+d*i)|*(cos p*cos q+(sen p*sen q)*(-1)+(cos p*sen q+sen p*cos q)*i)=
|(a+b*i)*(c+d*i)|*(cos p*cos q+(-sen p*sen q)+(cos p*sen q+sen p*cos q)*i)=
|(a+b*i)*(c+d*i)|*(cos p*cos q-sen p*sen q+(cos p*sen q+sen p*cos q)*i)=
|(a+b*i)*(c+d*i)|*(cos (p+q)+sen (p+q)*i)
Dalla proprietà sopra segue che (basta ripetere la moltiplicazione con termini tutti uguali)
(|a+b*i|*(cos p+sen p*i))n=|(a+b*i)n|*(cos (n*p)+sen (n*p)*i)
Vogliamo calcolare tutte le soluzioni di (|a+b*i|*(cos p+sen p*i))n=|c+d*i|*(cos q+sen q*i)
 (è l' equazione xn=z del sottotitolo)
Possiamo riscriverla come
|(a+b*i)n|*(cos (n*p)+sen (n*p)*i)=|c+d*i|*(cos q+sen q*i)
Questi 2 numeri complessi saranno uguali quando
|(a+b*i)n|=|c+d*i|
n*p=q.
Questo è equivalente a
(|a+b*i|)n=|c+d*i|
n*p=q.
Facendo pochi conti otteniamo
|a+b*i|=(|c+d*i|)
n*p=q.
L' angolo giro (l' angolo disegnato da una rotazione completa) misura 2. Ciò significa che se aumentiamo un' angolo di un multiplo di 2, otteremo sempre lo stesso angolo e i valori delle funzioni trigonometriche applicate a questi angoli saranno sempre gli stessi.
Quindi possiamo scrivere
n*p=q
n*p=q+2
n*p=q+4
...
n*p=q+k*2
...
n*p=q+(n-1)*2
Facendo pochi conti otteniamo
p1=q/n
p2=(q+2)/n
p3=(q+4)/n
...
pk=(q+k*2)/n
...
pm=(q+(n-1)*2)/n

La soluzione generica è data da |a+b*i|*(cos pk+sen pk*i)=(|c+d*i|)*(cos((q+k*2)/n)+sen((q+k*2)/n)*i)
Esempio:
x5=1
(|a+b*i|*(cos p+sen p*i))5=1
Usiamo una delle formule sopra
|(a+b*i)5|*(cos (5*p)+sen (5*p)*i)=1
Usiamo un' altra delle formule sopra
(|a+b*i|)5*(cos (5*p)+sen (5*p)*i)=1
Ora bisogna scrivere 1 in forma polare.
In questo caso è semplice, ma in generale è meglio disegnare il numero nel piano complesso; per calcolare il valore assoluto (che è la distanza dall' origine) si usa il teorema di Pitagora e per calcolare l' angolo si usano le regole generali della trigonometria.
Se disegno 1 nel piano complesso, noto che la sua distanza dall' origine è 1 e che l' angolo che forma il segmento congiungente esso e l' origine con la direzione positiva dell' asse reale è 0. Quindi
1=1*(cos 0+sen 0*i)
(Infatti 1*(cos 0+sen 0*i)=1*(1+0*i)=1*(1+0)=1*1=1.)
Quindi
(|a+b*i|)5*(cos (5*p)+sen (5*p)*i)=1*(cos 0+sen 0*i)
Questi 2 numeri complessi sono uguali quando
(|a+b*i|)5=1
5*p=0
Facendo pochi conti otteniamo
|a+b*i|=1
|a+b*i|=1
(ci basta 1 numero (non ci serve cercare gli altri che elevati alla 5 danno 1) perché il valore assoluto è sempre positivo e reale e poi tutti questi conti servono a calcolare proprio i numeri che elevati alla 5 danno 1)
Poi ci ricordiamo che
5p=0
5p=2
5p=4
5p=6
5p=8
Facendo pochi conti otteniamo
p1=0
p2=2/5
p3=4/5
p4=6/5
p5=8/5
Quindi le soluzioni sono date da
1(cos 0+sen 0*i)
1(cos (2/5)+sen (2/5)*i)
1(cos (4/5)+sen (4/5)*i)
1(cos (6/5)+sen (6/5)*i)
1(cos (8/5)+sen (8/5)*i)
Riscriviamole in modo ordinato
1
cos (2/5)+sen (2/5)*i
cos (4/5)+sen (4/5)*i
cos (6/5)+sen (6/5)*i
cos (8/5)+sen (8/5)*i

Questo metodo è assolutamente generale ma ha il grande svantaggio di darci le soluzioni in maniera non appropriata. A volte sappiamo calcolare i valori di seno e coseno delle soluzioni in termini di operazioni, ma molte volte no (come in questo caso). Sarebbe più opportuno scrivere le soluzioni esprimendole con operazioni piuttosto che con funzioni trigonometriche. È possibile farlo solo trattando questo problema come risoluzione di equazioni polinomiali, ma come abbiamo visto non è possibile sempre risolverle e ci vuole molto ingegno.
Comunque così si possono sempre ottenere delle soluzioni approssimate. Calcoliamole per l' esempio sopra.
1
~0,31+0,95*i
~-0,81+0,59*i
~-0,81-0,59*i
~0,31-0,95*i
Trovare le soluzioni di xn=1 con metodi per le equazioni polinomiali
 Non c' è un metodo generale, posso solo dare esempi!!!
Esempio:
x3=1
Facendo pochi conti otteniamo
x3-1=0
Evidentemente una soluzione è 1 (x1=1). 1 è anche la soluzione dell' equazione x-1=0, quindi il polinomio x3-1 è divisibile col polinomio x-1. Facciamo la divisione (ma in alternativa potremmo usare la regola 6 dei prodotti notevoli per scomporre il polinomio; in quel caso non serviva nemmeno conoscere una soluzione).
(x3-1)/(x-1)
(1x3+0x2+0x+(-1))/(x-1)
  -  1  0  0  - (-1)
1 -  0  1  1  - 1
---------------------
  -  1  1  1  - 0
(x3-1)/(x-1)=1x2+1x+1
(x3-1)/(x-1)=x2+x+1
Con pochi conti otteniamo
x3-1=(x2+x+1)(x-1)
Risolviamo x2+x+1=0
x=(±(12-4*1*1)-1)/(2*1)
x=(±(1-4)-1)/2
x=(±(-3)-1)/2
x=(±((-1)*3)-1)/2
x=(±(-1)*3-1)/2

x2=(i*3-1)/2
x2=(1/2)(i*3-1)
x2=(1/2)(-1+3*i)

x3=((-i)*3-1)/2
x3=((-1)*(i*3)-1)/2
x3=((-i*3)+(-1))/2
x3=(-1+(-i*3))/2
x3=(-1-i*3)/2
x3=(1/2)(-1-3*i)

Quindi x1=1, x2=(1/2)(-1+3*i), x3=(1/2)(-1-3*i).
Esempio:
x4=1
Facendo pochi conti otteniamo
x4-1=0
Adesso ricordiamo la regola 2 dei prodotti notevoli.
a2-b2=(a-b)(a+b)
Proviamo a trovare una regola per scomporre a2+b2 in 2 parti moltiplicate tra loro.
a2+b2=
a2+(-(-b2))=
a2-(-b2)=
a2-((-1)b2)1=
a2-((-1)b2)(1/2)2=
a2-(((-1)b2)1/2)2=
a2-(((-1)b2))2=
a2-((-1)b2)2=
a2-(i*(b2)1/2)2=
a2-(i*b2(1/2))2=
a2-(i*b1)2=
a2-(b*i)2=
usiamo la regola sopra
(a-b*i)(a+b*i)
 È bene ricordarsi questa regola appena ottenuta:
a2+b2=(a-b*i)(a+b*i)
 Quindi usando le ultime 2 regole possiamo scrivere:
x4-1=0
(x2-1)(x2+1)=0
(x-1)(x+1)(x-i)(x+i)=0
Le soluzioni delle equazioni
x-1=0
x+1=0
x-i=0
x+i=0
sono tutte le soluzioni dell' equazione di partenza.
Quindi
x1=1, x2=-1, x3=i, x4=-i.
Esempio:
x5=1
Facendo pochi conti otteniamo
x5-1=0
Evidentemente una soluzione è 1 (x1=1).
1 è anche soluzione dell' equazione polinomiale x-1=0.
Allora x5-1 è divisibile con x-1.
Uso l' algoritmo di Horner.
(x5-1)/(x-1)
(1x5+(-1))/(x-1)
  -  1  0  0  0  0  - (-1)
1 -  0  1  1  1  1  - 1
---------------------------
  -  1  1  1  1  1  - 0
Quindi
(x5-1)/(x-1)=1x4+1x3+1x2+1x+1
(x5-1)/(x-1)=x4+x3+x2+x+1
Con pochi conti otteniamo
x5-1=(x4+x3+x2+x+1)(x-1)
Cerchiamo le soluzioni (che sono le stesse dell' equazione polinomiale di partenza) di
x4+x3+x2+x+1=0
Per risolverla devo ricorrere ad alcuni stratagemmi.
x4+x3+x2+x+1=0 //x2
(x4+x3+x2+x+1)/x2=0/x2
x4/x2+x3/x2+x2/x2+x1/x2+1/x2=0
x4-2+x3-2+1+x1-2+1/x2=0
x2+x1+1+x-1+1/x2=0
x2+x+1+1/x1+1/x2=0
x2+x+1+1/x+1/x2=0
ecco lo stratagemma: faccio la sostituzione y=x+1/x
quindi y2=x2+2x(1/x)+(1/x)2
y2=x2+2*1+12/x2
y2=x2+2+1/x2
x2+2+1/x2=y2 /-2
x2+2+(-2)+1/x2=y2-2
x2+0+1/x2=y2-2
x2+1/x2=y2-2
ritorniamo all' equazione
x2+x+1+1/x+1/x2=0
(x2+1/x2)+(x+1/x)+1=0
(y2-2)+y+1=0
y2+y+1+(-2)=0
y2+y+(-1)=0
y2+y-1=0
1y2+1y+(-1)=0
y=(±(12-4*1*(-1))-1)/(2*1)
y=(±(1-(-4))-1)/2
y=(±(1+(-(-4)))-1)/2
y=(±(1+4)-1)/2
y=(±5-1)/2
y=(1/2)(±5-1)

y1=(1/2)(5-1)

y2=(1/2)(-5-1)

la sostituzione era y=x+1/x
y=x1+1/x
y=xx(1/x)+1/x
y=x2/x+1/x
y=(x2+1)/x /*x
xy=(x2+1)(1/x)*x
xy=(x2+1)1
xy=x2+1
x2+1=xy /-(xy)
x2+(-xy)+1=xy-xy
x2-xy+1=0
1x2+(-yx)+1=0
1x2+(-y)x+1=0
x=(±((-y)2-4*1*1)-(-y))/(2*1)
x=(±(((-1)*y)2-4)+(-(-y)))/2
x=(±((-1)2*y2-4)+y)/2
x=(±(1*y2-4)+y)/2
x=(±(y2-4)+y)/2
x=(1/2)(y±(y2-4))

x=(1/2)(y1±(y12-4))
y1=(1/2)(5-1)

x=(1/2)((1/2)(5-1)±(((1/2)(5-1))2-4))
x=(1/2)((1/2)(5-1)±((1/2)2(5-1)2-4))
x=(1/2)((1/2)(5-1)±((12/22)(5+(-1))2-4))
x=(1/2)((1/2)(5-1)±((1/4)((51/2)2+25(-1)+(-1)2)-4))
x=(1/2)((1/2)(5-1)±((1/4)(5(1/2)2+(-25)+1)-4))
x=(1/2)((1/2)(5-1)±((1/4)(51+1+(-25))-4))
x=(1/2)((1/2)(5-1)±((1/4)(5+1+(-25))-4*1))
x=(1/2)((1/2)(5-1)±((1/4)(6-25)-4*4*(1/4)))
x=(1/2)((1/2)(5-1)±((1/4)((6-25)-4*4)))
x=(1/2)((1/2)(5-1)±(1/4)(6-25-16))
x=(1/2)((1/2)(5-1)±(1/2)(6+(-16)+(-25)))
x=(1/2)(1/2)((5-1)±(6-16+(-25)))
x=(1/2)(1/2)(5-1±((-10)+(-25)))
x=(1/2)2(5-1±((-1)10+(-1)25))
x=(12/22)(5-1±((-1)2*5+(-1)25))
x=(1/4)(5-1±((-1)2(5+5)))
x=(1/4)(5-1±((-1)2(5+5)))
x=(1/4)(5-1±(-1)2(5+5))
x=(1/4)(5-1±i*2(5+5))

x2=(1/4)(5-1+i*2(5+5))
x3=(1/4)(5-1-i*2(5+5))

x=(1/2)(y2±(y22-4))
y2=(1/2)(-5-1)

analogamente a prima
x4=(1/4)(-5-1+i*2(5-5))
x5=(1/4)(-5-1-i*2(5-5))
Nota: per calcolare tutte le soluzioni di xn=a dove a è un numero reale è sufficiente calcolare tutte le soluzioni di xn=1. Infatti
Sia xk soluzione di xn=1.
(xk a)n=
xkn (a)n=
1 a=
a
 Si calcola solo a (è un numero) e lo si moltiplica con tutte le soluzioni di xn=1 ad una ad una.
Ecco i risultati che ho ottenuto tramite la risoluzione di equazioni polinomiali e alcuni stratagemmi (l' ordine delle soluzioni per ciascuna non è necessariamente corrispondente alla disposizione dei punti che rappresentano tali numeri nel piano complesso). Sfido chiunque a trovarne altri.
Per x10=1 e x20=1 non ho effettuato i conti, ma ho preso le soluzioni di x5=1, ho cambiato i + e i - in vari modi e ho aggiunto le soluzioni -1, i e -i, poi le ho confrontate con le approssimazioni ottenute dal metodo generale (l' idea mi è venuta capendo che le soluzioni di x5=1 sono anche soluzioni di x10=1 e x20=1).
x1=1
x1=1
x2=1
x1=1
x2=-1
x3=1
x1=1
x2=(1/2)(-1+3*i)
x3=(1/2)(-1-3*i)
x4=1
x1=1
x2=-1
x3=i
x4=-i
x5=1
x1=1
x2=(1/4)(-1+5+2(5+5)*i)
x3=(1/4)(-1+5-2(5+5)*i)
x4=(1/4)(-1-5+2(5-5)*i)
x5=(1/4)(-1-5-2(5-5)*i)
x6=1
x1=1
x2=-1
x3=(1/2)(1+3*i)
x4=(1/2)(1-3*i)
x5=(1/2)(-1+3*i)
x6=(1/2)(-1-3*i)
x8=1
x1=1
x2=-1
x3=i
x4=-i
x5=(2/2)(1+i)
x6=(-2/2)(1+i)
x7=(2/2)(-1+i)
x8=(-2/2)(-1+i)
x10=1
x1=1
x2=-1
x3=(1/4)(1+5+2(5-5)*i)
x4=(1/4)(-1+5+2(5+5)*i)
x5=(1/4)(1-5+2(5+5)*i)
x6=(1/4)(-1-5+2(5-5)*i)
x7=(1/4)(-1-5-2(5-5)*i)
x8=(1/4)(1-5-2(5+5)*i)
x9=(1/4)(-1+5-2(5+5)*i)
x10=(1/4)(1+5-2(5-5)*i)
x20=1
x1=1
x2=-1
x3=i
x4=-i
x5=(1/4)(1+5+2(5+5)*i)
x6=(1/4)(1+5-2(5+5)*i)
x7=(1/4)(1+5-2(5-5)*i)
x8=(1/4)(1+5+2(5-5)*i)
x9=(1/4)(1-5-2(5+5)*i)
x10=(1/4)(1-5+2(5+5)*i)
x11=(1/4)(1-5+2(5-5)*i)
x12=(1/4)(1-5-2(5-5)*i)
x13=(1/4)(-1+5+2(5+5)*i)
x14=(1/4)(-1+5-2(5+5)*i)
x15=(1/4)(-1+5-2(5-5)*i)
x16=(1/4)(-1+5+2(5-5)*i)
x17=(1/4)(-1-5-2(5+5)*i)
x18=(1/4)(-1-5+2(5+5)*i)
x19=(1/4)(-1-5+2(5-5)*i)
x20=(1/4)(-1-5-2(5-5)*i)

Mappa del sito