在人類的知識探求中,數量關係是最重要的研究課題之一。除了數學外,各門自然科學乃至某些社會科學的研 究目標也是探求存在於自然或社會現象中的數量關係。人們如何表達數量關係?除了使用數學公式外,還必須 使用自然語言中的各種「量詞」(Quantifier)(註1),例如數學上經常用到的「唯一一個」、「奇數 個」、「可數無限個」等等。除了這些在數學或自然科學上專門用到的「量詞」外,我們在日常語言中還會使 用其他「量詞」,例如「所有事物」、「大多數人」、「很多」、「整整一半」、「幾乎沒有」、「多於七成」 、「三至七個」等等(註2)。可以說,「量詞」是在語言學(特別是語義學)研究中與數學關係最密切的課題。事 實上,對某些「量詞」問題的研究推動了當今「形式語義學」(Formal Semantics)多個分支理論的形成和發展 ,其中尤以「廣義量詞理論」(Generalized Quantifier Theory)最為突出。「廣義量詞理論」雖然 是當代的產物,但其研究對象有很古老的歷史淵源,可以上溯至古希臘的形式邏輯,因此以下先從古典形式邏 輯有關「量化句」的理論開始談起。
由Aristotle開創的「古典形式邏輯」(Classical Formal Logic)的主要目的是尋求有效的推理形式 ,即從真前提必能推出真結論的推理形式。為此,古典形式邏輯研究了多種推理形式,包括對當關係推理、結 構變換推理、三段論推理、聯言推理、選言推理、假言推理等。以下僅介紹與「廣義量詞理論」有較密切關係 的對當關係推理和三段論推理。
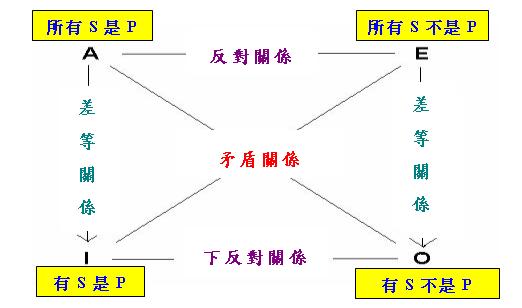
「對當關係」是指四個「量化句」(Quantified Sentence)之間的邏輯推理關係。後來有人把這些關 係總結為一個「對當方陣」(Square of Opposition),即以下的圖形(為區別下文將會介紹的其他類型的對當方 陣,現把下圖稱為「古典對當方陣」Classical Square of Opposition):

在上圖中,四個「量化句」分別由字母A、E、I、O代表,其中A和I是「肯定命題」(Affirmative Proposition)
,E和O是「否定命題」(Negative Proposition)(註3)。此外,A和E含有量詞「所有」(即英語的"all"或
"every"),合稱為「全稱命題」(Universal Proposition),I和O則含有量詞「有」(即英語的"some",意即「
至少有一個」),合稱為「特稱命題」(Particular Proposition)。四句中的S代表「主詞」(Subject),P代表
「謂詞」(Predicate),「是」則是「系詞」(Copula)。
除了四個「量化句」外,上圖還標示了四種推理關係:「矛盾(Contradictory)關係」、「反對(Contrary)關係
」、「下反對(Subcontrary)關係」和「差等(Subalternate)關係」,以下簡述這四種推理關係的意義。「矛盾
關係」是指若p真,則q假;若p假,則q真,反之亦然。「反對關係」是指p和q不可以同真,但可同假;因此當p
(或q)真時,q(或p)必假,但反之卻不必然。「下反對關係」是指p和q可以同真,但不可同假;因此當p(或q)假
時,q(或p)必真,但反之卻不必然。「差等關係」則相當於「單向蘊涵關係」,即如果p真,則q也真,但反之
卻不必然。人們可以利用這些關係進行某些推理,例如:
| 所有學生都穿校服 ⇔ 並非有學生不穿校服 | (矛盾關係) |
| 所有學生都穿校服 ⇒ 並非所有學生都不穿校服 | (反對關係) |
| 沒有學生穿校服 ⇒ 有學生不穿校服 | (下反對關係) |
| 所有學生都穿校服 ⇒ 有學生穿校服 | (差等關係) |
本文所稱的「三段論」推理是指古典形式邏輯研究得最多的「直言三段論」(Categorical Syllogism)推理(此 外,還有「假言三段論」、「模態三段論」等)。「直言三段論」就是由三個直言命題(Categorical Proposition)組成的推理,其中兩個是「前提」(分別稱為「大前提」Major Premise和「小前提」Minor Premise),最後一個是「結論」(Conclusion)。每個命題均由兩個詞項(Term)組成,即主詞和謂詞,三個命題 便共有六個詞項,其中「結論」的主詞和謂詞分別稱為「小項」(Minor Term)和「大項」(Major Term)。除了 出現在「結論」中外,「小項」和「大項」還分別在「小前提」和「大前提」中出現一次。此外,還有一個「 中項」(Middle Term),它在「小前提」和「大前提」中各出現一次。由於「直言三段論」的三個命題常常以量 化句的形式出現(註4),因此除了上述三個詞項外,一般還包含「所有」、「有」等詞項。以下例子說明以上提 到的各個概念:
| 大前提: | 所有人(中項)都是會死的(大項) |
| 小前提: | 所有希臘人(小項)都是人(中項) |
| 結論: | 所有希臘人(小項)都是會死的(大項) |
傳統邏輯學家的任務就是研究哪些推理模式是有效的。他們按照「中項」在兩個前提中可能出現的位置把「三 段論」分為四種「格」(Figure),例如上述「三段論」便屬於「第一格」。在每種「格」下,邏輯學家又按照 每個命題是屬於A、E、I、O的哪種句式而分為各種「式」(Form),例如上述「三段論」便屬於AAA式(俗稱 Barbara式),因為三個命題都是「全稱肯定命題」(即A句)。當然並非每種格式都是有 效的推理,例如以下的第二格OIE式便是無效的:
| 大前提: | 有動物(大項)不是被遺棄動物(中項) |
| 小前提: | 有貓(小項)是被遺棄動物(中項) |
| 結論: | 所有貓(小項)都不是動物(大項) |
古典形式邏輯學家的工作就是辨別哪些格式是有效的推理,並從中總結出一些「三段論規則」。
自Aristotle創立古典形式邏輯以後,西方的邏輯學者基本沿襲其邏輯系統,沒有作出重大更動。可以說西方邏
輯處於停滯狀態達十多個世紀之久。及至19世紀末,Boole、Peano、Frege、Russell等人開始把古典邏輯數學
化和嚴格化,形成「命題邏輯」(Propositional Logic)和「謂詞邏輯」(Predicate
Logic)。前者的研究對象是「邏輯聯結詞」(Logical Connective),包括「非」(~)、「和」(∧)、「或」
(∧)、「如果 ... 則」(⇒)、「當且僅當」(⇔)等。後者則是在前者的基礎上加上兩個代表「全
稱量詞」(Universal Quantifier,相當於自然語言中的「所有」、「每個」等)和「特稱量詞」(Particular
Quantifier,又稱「存在量詞」Existential Quantifier,相當於自然語言中的「有」、「至少有一個」等)的
符號∀和∃,並把古典邏輯的A、E、I、O「翻譯」成包含「邏輯聯結詞」和上述量詞符號的表達式
。具體地說,「所有S是P」可表達成∀x(S(x) ⇒ P(x)),用日常語言說出來就是「對(論域中)所有
個體x而言,如果S(x),則P(x)」。這裡S和P均被處理成「謂詞」,用數學的術語說則是「函項」(Function),
而x則是「論元」(Argument,或譯作「主目」),「S(x)」的意思是x具有S這種屬性(註5)。類似地,「有S是P」
則可表達成∃x(S(x) ∧ P(x)),用日常語言說出來就是「(在論域中)存在(至少一個)個體x,使得
S(x)並且P(x)」。透過這樣的定義,「謂詞邏輯」遂從古典邏輯的量化句中把「量詞」抽離出來,並以此作為
研究對象,因此「謂詞邏輯」又稱「量化理論」(Quantification Theory)。
我們亦可以用集合論語言來重新表述上段的「謂詞邏輯」語句。一般認為,邏輯與集合論有相通之處,因此兩
者的概念常可互相定義。例如,我們可以把某函項P看成集合P',把具有某函項P所述性質的個體x看成集合P'的
元素,即P(x) ⇔ x ∈ P'。反之,我們亦可以透過「特徵函項」(Characteristic Function)把某集
合S看成函項S',即若x ∈ S,S'(x) = 1 (或簡寫作S'(x));若x ~∈ S,S'(x) = 0 (或簡寫作
~S'(x))。基於上述對應關係以及集合「包含」(Inclusion)的定義,我們便可以把「全稱命題」
∀x(S(x) ⇒ P(x))用集合論語言重新表述為S ⊆ P。同理,根據集合「交」(Intersection)運
算的定義,我們亦可以把「特稱命題」∃x(S(x) ∧ P(x))重新表述為S ∩ P ≠ Φ (這裡
Φ代表「空集」)。
現代數理邏輯不僅研究上述的「邏輯聯結詞」和「量詞」,而且更重要的是建構邏輯推理系統,並研究這些系
統的各種「元邏輯(Metalogical)性質」,例如「真確性」(Soundness)、「完備性」(Completeness)、「無矛
盾性」(Consistency)等。這一方面使古典形式邏輯的各種推理統一在同一個邏輯推理系統之下,人們無需再分
門別類地逐一學習這些推理(因為這些傳統推理的很多結果都已成為同一個邏輯推理系統之下的「定理」);但
另一方面亦使數理邏輯研究與自然語言推理的距離越拉越遠。
現代數理邏輯不僅沒有擴充「古典對當方陣」,而且還由於它把「全稱量詞」定義成蘊涵式(即包含「如果 ...
則」的表達式),結果使「古典對當方陣」中的某些推理關係變成無效。根據「命題邏輯」對「蘊涵」
(Implication)的定義,當蘊涵式的前件(即前提)假時,則無論其後件(即結論)是真還是假,整個蘊涵式自然是
真的。這樣,根據「所有S是P」的邏輯表達式∀x(S(x) ⇒ P(x)),如果在論域中根本沒有x ∈
S (即S(x)對所有x而言都是假的),則整個蘊涵式(即「所有S是P」)自然是真的。換句話說,即使S是空集,「
所有S是P」仍是真的。由於容許「所有S是P」中的S為空集,我們便不能從「所有S是/不是P」推出「有S是/
不是P」。而且,根據前述「蘊涵」的定義,當S是空集時,不僅「所有S是P」自然真,「所有S不是P」也自然
真,即「所有S是P」與「所有S不是P」可以同真。同理,當S是空集時,「有S是P」與「有S不是P」便同假。總
上所述,在現代數理邏輯的「蘊涵」定義下,「古典對當方陣」中的「差等關係」、「反對關係」和「下反對
關係」都不再成立,只有「矛盾關係」仍然成立。這樣,「古典對當方陣」便變成了以下的「布爾對當方陣」
(Boolean Square of Opposition),從而大大減損了傳統對當關係推理的內容。

雖然謂詞邏輯在形式化和推理的嚴密性方面大大超越了古典形式邏輯,但它所能表達的量詞種類卻仍然很有限
。謂詞邏輯可以透過增加一個「等詞」(即等號「=」),變成「帶等詞的謂詞邏輯」(Predicate
Logic with Equality),以表達「有定摹狀詞」(Definite Description,即含有英語「定冠詞」"the"的名詞
短語)以及「至少n個」、「最多n個」或「剛好n個」等意思,但其表達法非常累贅。例如「剛好兩個S是P」便
要表達為∃x∃y(x ≠ y ∧ S(x) ∧ P(x) ∧ S(y) ∧ P(y) ∧
∀x∀y∀z(S(x) ∧ P(x) ∧ S(y) ∧ P(y) ∧ S(z) ∧ P(z)) ⇒
((x = y) ∨ (y = z) ∨ (z = x))),用日常語言說出來就是「(在論域中)存在兩個不相同的個體x和y使
得x和y都同時具有S和P的屬性,並且對(論域中)任何三個個體x、y和z而言,如果x、y和z都同時具有S和P的屬
性,那麼x、y和z三者之中必有至少兩個是相同的」。上述這種定義方法就像是繞了一個大彎來說明何謂「剛好
兩個S是P」,與我們的直觀理解相差甚遠。
不過上述問題還不是謂詞邏輯(嚴格地說,應是「一階謂詞邏輯」First Order Predicate Logic)的
致命缺點,因為邏輯學家大可創作一些新的符號來代表上段所述的那些新量詞,例如用∃!來代表「有定
摹狀詞」,用∃=2來代表「剛好兩個」等等,這樣便可以把「剛好兩個S是P」記為
∃=2x(S(x) ∧ P(x))。當然邏輯學家還要定義新的公理或推理規則,才能對這些新的量
詞進行推理。這些都不是問題,真正的問題是「一階謂詞邏輯」無法表達很多在數學上和自然語言中經常要用
到的量詞(例如「奇數個」、「偶數個」、「有限個」、「可數無限個」、「不可數無限個」等)以及某些涉及
數量比例的量詞(如「多數」、「多於三成」等),更遑論一些結構較為複雜的量詞(例如英語的"more than m
of the n")了,這充分說明「一階謂詞邏輯」的表達力不夠強。很明顯,如要表達及研究自然語言中的更多量
詞,我們需要一種表達力更強的邏輯工具。
為了能把古典形式邏輯以及上述「帶等詞的謂詞邏輯」的原有量詞擴充至存在於數學和自然語言中的其他量詞
,人們須先對量詞所代表的邏輯性質有清楚的認識。邏輯學家(以至一般人)對於理解專有名詞和動詞的邏輯性
質一般都沒有太大困難。在現代邏輯系統下,動詞被理解成含有一至三個論元的函項(註6),而專有名詞則被理
解成論元。舉例說,句子「John愛Mary」便可以表達為LOVE(j, m),其中LOVE為二元函項,j和m為論元。
現在我們把3.1節提過的函項與集合之間的對應關係加以推廣:「論元」相當於某一「論域」(Universe of
Discourse)下的「元素」(Element);「一元函項」相當於由元素組成的「集合」(Set);「二/三元函項」則
相當於由「有序對」(Ordered Pair)/「有序三元組」(Ordered Triple)組成的集合。舉例說,前述的句子「
John愛Mary」用集合論語言表達就是(j, m) ∈ LOVE。這裡LOVE是由有序對組成的集合,而(j, m)則是有
序對。
可是我們又應如何理解量詞呢?以「全稱量詞」為例,前面說過語句「所有S是P」可以用謂詞邏輯和集合論語
言分別表達為∀x(S(x) ⇒ P(x))和S ⊆ P,那麼全稱量詞「所有」似乎等於∀或⊆
,亦即謂詞邏輯和集合論上的「算子」(Operator)。可是把量詞理解為「算子」只是給它們加一個「別名」或
「標籤」而已,並沒有實質弄清楚它們的性質,因此我們還要進一步探索這一個問題。
其實,在「廣義量詞理論」正式誕生之前,有一些邏輯學家已初步具備「廣義量詞」概念的萌芽。現代數理邏
輯的奠基人之一Frege便把量詞視為「第二層次概念」(Second-Level Concept),有別於作為「第一層次概念」
(First-Level Concept)的普通謂詞。從集合的角度看,如果作為「第一層次概念」的謂詞被理解成集合,那麼
作為「第二層次概念」的量詞便應理解成「集合的集合」(Set of Sets),或稱「集合族」(Family of Sets)。
到20世紀中葉以後,邏輯學家Mostowski把Frege的思想具體化。他把某一論域U下的量詞定義為該論域的子集的 集合(註7),亦即Power(U)的子集(註8)。在他的理論中,「全稱量詞」和「特稱量詞」可以分別表述為
| ∀U = {U} | (1) |
| ∃U = {B ⊆ U: B ≠ Φ} = Power(U) − {Φ} |
這裡∀和∃帶有下標U是因為這兩個量詞在不同的論域U下有不同的「所指」(Denotation),即代表
不同的「集合族」(但其意義相同)。視乎U是代表人或事物的集合,以上兩個量詞分別代表英語的代名詞
"everybody"或"everything" (相當於漢語的「所有人」或「所有東西」)和"somebody"或"something" (相當於
漢語的「有人」或「有東西」)。以上所列只是Power(U)的其中兩個子集,但Power(U)還可以有其他子集,
Power(U)的每一個子集都可以定義一個量詞(當然並非所有這樣的量詞都在自然語言中有對應的詞項),這樣便
大大擴充了量詞的範圍。
此外,Mostowski還定義了量詞的真值條件(以下略作簡化):設QU為論域U下的量詞,P為謂詞變項
,x為個體變項,則
其實如果P不涉及其他個體變項,我們大可以把上式中的x略去,因為量詞作為「第二層次概念」,只與作為「 第一層次概念」的謂詞直接發生關係,因此上式可改寫為
在上述定義下,量詞QU類似一個「二階謂詞」,而普通的謂詞(即「一階謂詞」) P則成了 QU的論元。從集合的觀點看,P代表集合,QU則代表集合族。現以一個日常語言的句子 為例,假設論域U為人的集合,則語句「有人唱歌」(即「有唱歌者」)便可以表述為
即「有人唱歌」的意思就是「唱歌者的集合不是空集」,這顯然是合理的。
Mostowski雖然找到了量詞的正確定義,但他所研究的量詞還只是論元結構較簡單的量詞。後來Lindstrom把 Mostowski的定義推廣到更一般的情況,並正式使用「廣義量詞」(Generalized Quantifier)的名稱 (以下為行文方便,有時把「廣義量詞」簡稱為「量詞」)。Lindstrom所研究的量詞的論元結構遠較Mostowski 的量詞複雜,可稱為「k位量詞」(k-Place Quantifier)(註9)。若把他的定義加以簡化,並略去個體 變項,則有以下「k位量詞」的真值條件:設QU為「k位量詞」,它含有k個謂詞P1、 P2 ... Pk作為其論元,每一個謂詞Pi (1 ≤ i ≤ k)不必都是一元 謂詞,而可以是ni元謂詞(ni為任意正整數),而且這些ni可以各不相同, 於是我們有
上式右端顯示QU是由「有序k元組」(P1, P2 ... Pk)組成的
集合,而每一個Pi本身又是由「有序ni元組」組成的集合。比較(2)和(3),容易看到
前述Mostowsi定義的量詞其實就是「1位量詞」。
由於定義(3)頗為複雜,以下先提供兩個較簡單的例子:
| allU = {(A, B) ⊆ U × U: A ⊆ B} | (4) |
| someU = {(A, B) ⊆ U × U: A ∩ B ≠ Φ} |
以上兩個都是「2位量詞」,它們都各自含有2個一元謂詞。這兩個量詞可分別用來表達英語「限定詞」
(Determiner) "all"或"every"(相當於漢語的「所有」或「每個」)和"some"(相當於漢語的「(至少)有(一個)」
)的意思。
請注意上文定義的∀U和∃U分別與allU和someU
存在一定聯繫,因為我們可以把(1)修改為
| ∀U = {B ⊆ U: U ⊆ B} = {U} | (5) |
| ∃U = {B ⊆ U: U ∩ B ≠ Φ} = Power(U) − {Φ} |
比較(4)和(5),容易看到以下等價關係:
以上等價關係其實反映了自然語言中某些「1位量詞」與「2位量詞」之間的聯繫(例如英語中"everybody" /
"everything"與"every"以及"somebody" / "something"與"some"之間的聯繫)(註10)。
自然語言中某些較為複雜的量化結構其實都可以抽象為某種「k位量詞」。例如從以下兩句
| More students than teachers sang. | (6) |
| Every student loves some teacher. |
我們可以分別抽象出以下兩個量詞:
| (more ... than ...)U = {(A, B, C) ⊆ U × U × U: |A ∩ C| > |B ∩ C|} | (7) |
| (every ... some ...)U = {(A, B, R) ⊆ U × U × U2: A ⊆ {x: {y: R(x, y)} ∩ B ≠ Φ}} (註11) |
上面兩個都是「3位量詞」,其中第一個量詞的3個論元都是一元謂詞;第二個量詞的前兩個論元是一元謂詞, 第三個論元則是二元謂詞(因此這個量詞是註9中所稱的「多式量詞」)。定義(7)看來頗為複雜,但只要我們把 U定義為人的集合,並把謂詞STUDENT、TEACHER、SING和LOVE代入適當的論元位置,然後細心理解這些形式語言 所代表的意義,便能看出上述定義的確反映了(6)中兩句的意思(註12):
上面第一式表示唱歌學生的數目多於唱歌教師的數目;第二式則表示所有學生都屬於某一類人,這一類人中的
每一個都愛至少一名教師。這正是(6)中兩句的意思(註13)。自然語言中還有其他更複雜的量化結構,這將留待
以後再介紹。
Mostowski和Lindstrom雖然已明確「廣義量詞」的定義,但在此時期的學者的研究重點乃在於與數學或數理邏
輯有密切關係的量詞,其中有些量詞甚至沒有自然語言的簡單對應表達式,例如以下這兩個量詞:
可以說,在此時期「廣義量詞」主要是應用於形式語言(即數學和邏輯學的語言)而非自然語言,這種情況直至 1970年代初Montague創立「蒙太格語法」才有所改變。
Montague作為一位邏輯學家,利用數理邏輯的方法來處理自然語言的語義問題,結果創立了「蒙太格語法」
(Montague Grammar)(他的理論重點其實不在「語法學」而是在「語義學」方面),並成為當代「形式語義
學」的鼻祖。Montague對「形式語義學」有多方面的貢獻,這裡只介紹他對量詞的處理方法。Montague在其名
篇The Proper Treatment of Quantification in Ordinary English (一般俗稱「PTQ」)一文中,把某
些類型的英語句子翻譯成「內涵邏輯」(Intensional Logic)表達式,然後透過對這些表達式的語義解釋,間接
地為他所研究的英語句子類型建立了一套語義理論。Montague語義理論的其中兩項特點是「類型論」(Type
Theory)和「λ演算」(λ-Calculus)方法的運用。
「類型論」的目的是為每一合式的「內涵邏輯」表達式提供一個適當的語義類型,從而確定各種表達式之間的
邏輯關係(特別是函項-論元關係)。撇除PTQ中與「內涵邏輯」有關的部分(註14),在PTQ中共有兩種基本的語義
類型:e和t,前者代表「個體」(Entity),即「一階謂詞邏輯」中「專有名詞」的語義類型;後者代表「真值」
(Truth Value),即「句子」的語義類型。其他表達式的語義類型都被處理成函項,並由e和t派生而成,例如「
不及物動詞」的語義類型是e → t,即由個體映射到真值的函項(這裡用符號「→」代表「映射」
Mapping),這是因為當一個不及物動詞與一個個體論元結合後,便會得到一個句子。這種處理方法也跟前面4.1
節所述「一階謂詞邏輯」把動詞理解成函項的方法相一致。
這裡無意詳細介紹PTQ中各種「內涵邏輯」表達式的語義類型,只想指出Montague區別處理「帶有限定詞的名詞
短語」和「不帶限定詞的名詞短語」(在PTQ中稱為「普通名詞短語」Common Noun Phrase)。這是因為在英語中
前者可以充當主語和賓語,而後者則不能,例如"boy"這個詞便不能作主語或賓語,必須加上限定詞變成"a
boy"、"the boy"等才行(請注意PTQ只研究單數名詞)。Montague把「普通名詞短語」的語義類型處理成跟不及
物動詞一樣,即e → t。這是因為從集合論的角度看,「普通名詞短語」跟不及物動詞一樣都可看成由元
素組成的集合。
至於「帶有限定詞的名詞短語」,Montague則把其語義類型確定為(e → t) → t。由於不及物動詞的
語義類型是e → t,所以「帶有限定詞的名詞短語」的語義類型就是把不及物動詞映射到真值的函項。為
何Montague要這樣確定「帶有限定詞的名詞短語」的語義類型?這是因為這種短語其實跟"everyone"、
"something"等代名詞具有相同的語義類型,何以見得?這可以從兩方面去看。首先,從構詞上看,我們可以把
"everyone"、 "something"等詞分拆成"every one"、"some thing",因此這些代名詞其實跟"every student"、
"some teacher"等「帶有限定詞的名詞短語」具有相同的結構。其次,從邏輯上看,我們可以把"everyone"與
"every student"以及"something"與"some teacher"的區別看成兩者「論域」的大小不同,即把"every
student"中的"student"以及"some teacher"中的"teacher"看成「論域」。這樣我們便可以分別用
∀U和∃U來表示"every student"和"some teacher"的意思,只須把這裡
的U分別解釋成「學生」和「教師」的集合便行了。
根據前面4.2節,Mostowski把∀U和∃U的語義「所指」確定為「集合族」
,因此「帶有限定詞的名詞短語」的語義「所指」也應是「集合族」,即「集合的集合」。根據3.1節所述函項
與集合之間的對應關係,以個體為元素的集合可被視為從個體集映射到真值的函項(參見註(5)),即其類型為e
→ t,那麼由於「集合的集合」是以集合為元素的集合,因此它應被視為從e → t這個函項的「值域」
(Range)映射到真值的函項,即其類型為(e → t) → t。這就是把「帶有限定詞的名詞短語」的語義
類型定為(e → t) → t的原因。
上述處理手法的一個結果是,所有跟「帶有限定詞的名詞短語」具有相同語法功能(即能夠充當主語和賓語)的
詞項(包括專有名詞和人稱代名詞)的語義類型也應為(e → t) → t。可是這麼一來,Montague對專有
名詞的處理手法便跟「一階謂詞邏輯」完全相反。如前所述,本來「一階謂詞邏輯」是把代表個體的專有名詞
處理成不及物動詞的「論元」,因此它的類型本應是t;可是PTQ卻把專有名詞的類型定為(e → t) →
t,這樣專有名詞與不及物動詞的角色顛倒了:如今是專有名詞成為「函項」,而不及物動詞反倒成了專有名詞
的「論元」。不過,Montague的這種處理手法有其合理性,因為在自然語言中,我們常常可以用連詞把專有名
詞與「帶有限定詞的名詞短語」構成並列短語,例如句子"John and a girl love each other."中的"John and
a girl"。一般而言,只有具有相同語義類型的詞項才可構成並列短語,Montague的處理手法能夠容易解釋為何
"John"與"a girl"可以構成並列短語。
解決了「帶有限定詞的名詞短語」的語義類型,我們便容易求得「限定詞」的語義類型。本來根據上面的定義 (4),在句子"Every student talked."中,名詞"student"和動詞"talked"同時作為「限定詞」"every"的論元 ,即這句的邏輯結構應為
不過,Montague基於「組合性原理」(Principle of Compositionality)(註15)的考慮,認為上句的邏輯結構應 為
即「限定詞」"every"只以名詞"student"為論元,構成一個「帶有限定詞的名詞短語」,然後這個短語"every student"以動詞"talked"為論元,構成整個句子。在此一觀點下,「限定詞」就是從「普通名詞短語」映射到 「帶有限定詞的名詞短語」的函項。由於如前所述,「普通名詞短語」的語義類型為e → t,所以「限定 詞」的語義類型應為(e → t) → ((e → t) → t)。
接著介紹Montague所用的「λ演算」方法。「λ演算」包括「λ抽象」 (λ-Abstraction)和「λ還原」(λ-Reduction)兩種運算,前者的實質是把一個句子轉化 為一個函項。舉例說,我們可以對句子「John愛Mary」的邏輯式LOVE(j, m)中的m進行抽象,即用變項x代替式 中的m,並且在上式的前面加上λx,從而得到λx[LOVE(j, x)],意即「John所愛的事物」,亦即 相當於集合論表達式{x: LOVE(j, x)}。請注意此兩式何其相似!根據前述集合與函項的對應關係,上述 λ表達式其實相當於一個函項。而「λ還原」則是「λ抽象」的逆運算,它相當於把一個 常項代入函項中。例如當我們把函項λx[LOVE(j, x)]作用於常項m時,我們便把m代入前式中的x並刪去 λx,從而得LOVE(j, m),即
用集合論語言表達,這等於說m ∈ {x: LOVE(j, x)},把m代入上述集合定義中的x同樣得到LOVE(j, m)。
Montague用「λ抽象」方法來表達「帶有限定詞的名詞短語」和「限定詞」的語義。以句子"Every
student talked."為例,在「一階謂詞邏輯」中,該句的表達式為
Montague一方面希望保留此一表達式,但另一方面又想貫徹「組合性原理」,為上句的各個組件"every student"、"talked"、"every"等各提供一個邏輯表達式,而且要能體現出各個表達式之間的函項-論元關係。 可是上式是一個整體,我們無法從它抽離出某些組件,例如我們不能說在上式中「∀x(STUDENT(x) ⇒」就是"every student"的邏輯表達式,因為這個符號串不是邏輯上的合式公式。為了解決這個問題, Montague巧妙地運用「λ抽象」,對上式中的TALK進行抽象,得到下式:
上式就是「名詞短語」"every student"的λ表達式,它代表一個把一元謂詞(即e → t)映射到真值 的函項,因此上式符合前述「帶有限定詞的名詞短語」的語義類型(e → t) → t。如果我們把上式作 用於一元謂詞TALK (即進行「λ還原」),便得到
請注意上式右端與(10)完全相同。由此可見(11)是"every student"的正確表達式。
前面說過,Montague把專有名詞與「帶有限定詞的名詞短語」等量齊觀,因此專有名詞也應有類似(11)的
λ表達式。以句子"John talked."為例,由於其「一階謂詞邏輯」表達式為TALK(j),只要我們對此式中
的TALK進行「λ抽象」,便可得到專有名詞"John"的λ表達式:
至此我們看到一個有趣現象,在「蒙太格語法」中,專有名詞"John"有兩種表達法和語義類型。當我們要獨立 提到它時,它的表達式是λB[B(j)],其語義類型為(e → t) → t;但當它出現在一個完整句 子中時,它的表達式卻是j,其語義類型為e。此一現象就是「形式語義學」中所稱的「類型轉換」 (Type-Shifting)。
利用「λ抽象」,我們可以進一步求得「限定詞」的λ表達式。舉例說,只要我們對(11)中的 STUDENT進行「λ抽象」,便可得到下式:
上式就是「限定詞」"every"的λ表達式,它代表一個把一元謂詞映射到(e → t) → t的函項
,因此上式符合前述「限定詞」的語義類型(e → t) → ((e → t) → t)。
基於相同原理,Montague亦根據含有「限定詞」"a"和"the"的語句的「一階謂詞邏輯」表達式求得這兩個「限
定詞」的λ表達式(Montague用"a"代表「特稱量詞」,即前面的"some"):
請注意在上面第二式中的∀x(A(x) ⇔ x = y)是用來表達在論域中具有A這種性質的個體是唯一的, 以反映"the"這個詞所含有的「唯一性」意義,這是自Russell以來對"the"這個詞的一種常見語義解釋。
在1980年代初,Barwise和Cooper發表Generalized Quantifiers and Natural Language一文,這是「
廣義量詞理論」中的另一篇代表作。他們一方面秉承Montague的某些思想,把「帶有限定詞的名詞短語」視為
一個語義單位,把它們稱為「量詞」(註17),並把專有名詞也歸入「量詞」的範圍。他們也把「量詞」的語義
類型確定為「集合族」,並確定其真值條件。
不過,另一方面,他們並不採納Montague保留「一階謂詞邏輯」表達式的做法,這是因為如前面3.2節所說,「
一階謂詞邏輯」的表達力不夠強,而且有些表達式過於繁瑣。舉例說,如果用Montague的方法寫出「剛好兩個」
的λ表達式,式子會非常冗長。因此,Barwise和Cooper採用集合論語言定義「量詞」,這是因為集合論
語言(註18)具有以下優點:一方面它具有數學的形式化特點,方便進行形式化定義和推導;另一方面它又較「
一階謂詞邏輯」直觀和靈活,較易為人理解。它的靈活性在於,在定義集合時沒有嚴格規定所用的語言,人們
隨時可以使用通用的數學或邏輯符號(例如表達集合基數Cardinal,即集合元素個數的符號| |),或者臨時定義
一個謂詞或函項,或甚至使用日常語言。舉例說,"all students"、"exactly two teachers"、"a finite
number of integers"和"John"等「量詞」的真值條件便可以分別定義為(在以下定義中B代表謂詞,即論域U下
的一個集合):
| (all students)U(B) ⇔ B ∈ {Y ⊆ U: STUDENT ⊆ Y} | (12) |
| (exactly two teachers)U(B) ⇔ B ∈ {Y ⊆ U: |TEACHER ∩ Y| = 2} | |
| (a finite number of integers)U(B) ⇔ B ∈ {Y ⊆ U: |INTEGER ∩ Y|是 有限數} | |
| JohnU(B) ⇔ B ∈ {Y ⊆ U: j ∈ Y} |
上面的真值條件在實質上跟前述Mostowski的真值條件(2)完全相同。不過,Barwise和Cooper所研究的「量詞」
包含「帶有限定詞的名詞短語」和專有名詞,因此較Mostowski的研究增加了內容。以專有名詞"John"為例,以
往「一階謂詞邏輯」是把專有名詞處理成個體,作為謂詞的論元,從集合論上看即是元素,因此句子"John
talked"要表達成j ∈ TALK,用日常語言說就是「John屬於TALK這個集合」或「John具有TALK這種性質/
行為」。但現在根據上述定義,JohnU變成「集合的集合」,即「John所具有的性質/行為的集合」
。這樣句子"John talked"要表達成TALK ∈ JohnU,用日常語言說就是「TALK屬於John所具有
的性質/行為之一」。十分有趣的是,我們在上述定義中也看到上面4.4.4節所述的「類型轉換」,就是"John"
這個詞具有雙重性質:一方面它表現為JohnU,即「集合的集合」;但另一方面它又可表現為j,即
元素。
其他「量詞」的語義解釋跟專有名詞類似,也是「集合的集合」,例如(exactly two teachers)U
的意思就是「剛好兩名教師所具有的性質/行為的集合」。這樣句子"Exactly two teachers sang."就要表達
成SING ∈ (exactly two teachers)U,用日常語言說就是「SING屬於剛好兩名教師所具有的
性質/行為之一」。
在上面我們把「限定詞」"all"、"exactly two"、"a finite number of"等與其後的名詞視為一個單位,即「 帶有限定詞的名詞短語」。但其實我們也可以把「限定詞」抽離出來,方法是把(12)中的名詞"students"、 "teachers"、"integers"等抽象成謂詞變項。這樣我們便可得到這些「限定詞」的真值條件:
| [allU(A)](B) ⇔ B ∈ {Y ⊆ U: A ⊆ Y} | (13) |
| [(exactly two)U(A)](B) ⇔ B ∈ {Y ⊆ U: |A ∩ Y| = 2} | |
| [(a finite number of)U(A)](B) ⇔ B ∈ {Y ⊆ U: |A ∩ Y|是有限數} |
根據上述定義,「限定詞」就是把集合(即定義中的A)映射到「集合族」(即「帶有限定詞的名詞短語」)的函項
。舉例說,假如我們把集合STUDENT代入上面allU的論元A,便會得到(12)中的
(all students)U。
請注意「集合族」可以被看成把集合映射到真值的函項,例如allU(A)本身也是一個函項,它也有
一個論元(即上面定義中的B)。因此上述定義是把「限定詞」看成一種「雙層函項」,這是「廣義量詞理論」對
「限定詞」的第一種語義解釋。以上面第一個定義為例,其內層函項為allU,它以A為論元;當這
個函項與A結合後便得到外層函項allU(A),它以B為論元。
可是,根據註(16),我們可以把「雙層函項」重新理解為含有兩個論元的「單層函項」。舉例說,我們可以把
(13)中的第一個定義改寫為
但上式還可以進一步化簡為
同理,(13)中的其餘兩個定義亦可以改寫為
這樣我們便可以把「限定詞」的語義理解為兩個集合A和B之間的關係,這是「廣義量詞理論」對「限定詞」的
第二種語義解釋。
上述兩種語義解釋雖然是等價的,但各有不同的用處。第一種語義解釋的結構較為複雜(表現為「雙層函項」)
,但它較符合自然語言的語法結構,因為(13)中的各行可以進一步抽象化為[D(A)](B) (D代表「限定詞」),而
其中的D(A)和B其實分別對應於自然語言中的主語和謂語,因此把D和A先合成一個單位,然後再與B結合,較能
準確反映自然語言句子的主謂結構。因此Barwise和Cooper在其形式語言系統L(GQ)中,也是採取[D(A)](B)的結
構。第二種語義解釋的結構則較為簡單,較適合用於進行計算或推理,所以後來的學者在研究「限定詞」時,
大多使用這種語義解釋。
上兩小節的內容主要是繼承和發展Mostowski、Lindstrom和Montague的原有理論。但除此以外,Barwise和 Cooper對「廣義量詞理論」也有新的貢獻。Barwise和Cooper提出了「量詞」的某些性質,例如「邏輯性」 (Logicality)、「駐留性」(Live-on)、「單調性」(Monotonicity)、「對偶性」(Duality)等(註19)。特別是 有關「單調性」和「對偶性」的研究揭示了某些古典形式邏輯和現代數理邏輯都沒有研究的自然語言推理, 例如:
| 所有學生都穿校服 ⇒ 所有男生都穿校服 | (左單調性推理) |
| 有學生穿冬季校服 ⇒ 有學生穿校服 | (右單調性推理) |
| 並非過半數人走了 ⇔ 至少一半人沒有走 | (對偶性推理) |
此外,Barwise和Cooper還嘗試總結出「量詞」的某些「普遍性質」(Universal),例如他們便提出以下這條(未 經證明)的「普遍性質」:「任何自然語言的簡單名詞短語都表達單調量詞或單調量詞的合取」。此外,他們還 在論文中提出多條命題和定理,並附有數學證明,使「廣義量詞理論」儼然成為一個獨立的數理邏輯學科。因 此可以說,他們的理論標誌著「廣義量詞理論」的最終形成。
從1980年代起,「廣義量詞理論」獲得長足發展,大批語言學家和邏輯學家加入研究行列,使這套理論成為「 形式語義學」中僅次於「蒙太格語法」的最重要分支學科。以下僅就筆者的有限知識,簡述「廣義量詞理論」 在不同方面的發展。以下的介紹將含有很多本文不會解釋的概念,其中某些概念將留待以後再介紹。
繼Barwise和Cooper之後,很多學者廣泛挖掘自然語言中各種量詞,並進行深入研究,使「廣義量詞理論」涵蓋 的量詞範圍得到空前膨脹。某些結構複雜或存在語義疑難問題的量詞或量化結構更成為眾多學者的研究熱點, 例如「所有格結構」(Possessive Construction)、「部分格結構」(Partitive Construction)、「比較結構」 (Comparative Construction)、「例外結構」(Exceptive Construction)、「模糊量詞」(Fuzzy Quantifier) 、「統指量詞」(Collective Quantifier)、「結構化量詞」(Structured Quantifier)以及各種「多式量詞」 (參見註9的定義),如「迭代量詞」(Iterated Quantifier)、「概括量詞」(Resumptive Quantifier)、「累指 量詞」(Cumulative Quantifier)、「分枝量詞」(Branching Quantifier)、「相互量詞」(Reciprocal Quantifier)等。此外,根據「生成語法」(Generative Grammar)有關「邏輯式」(Logical Form)的理論,「疑 問詞」(Interrogative)也可被看成一種「準量詞」(Quasi-Quantifier)。可是,對「疑問詞」的研究卻似乎是 「廣義量詞理論」的薄弱環節,較少學者問津。不過,筆者相信隨著「廣義量詞理論」研究的進一步深入,此 一情況將來也會有所改觀。
除了Barwise和Cooper提出的幾種量詞性質外,後來的學者繼續廣泛挖掘各種量詞的性質,如「守恆性」 (Conservativity)、「同構封閉性」(Isomorphism Closure)、「擴展性」(Extension)、「相交性」 (Intersectivity)、「對稱性」(Symmetry)、「基數性」(Cardinality)、「類可歸約性」(Sortal Reducibility)等。對於一些Barwise和Cooper已提出的量詞性質,後來的學者也繼續深入研究。例如「單調性 」便是一個研究熱點,有些學者在原來左、右單調性的基礎上,又提出某些新的單調性概念以及一個與「單調 性」密切相關的「光滑性」(Smoothness)概念。除了量詞性質外,很多學者亦研究各種對量詞的操作,包括「 關係化」(Relativization)、「限制」(Restriction)、「凍結」(Freezing)等。對這些性質和操作的研究, 使「廣義量詞理論」並非只停留於對量詞的分類或個別詞項的語義研究,而是以尋求量詞的普遍性質為研究目 標,從而成為一門真正的科學學科。
前文提過,現代數理邏輯的興起使古典形式邏輯研究的課題失去獨立意義,逐漸成為一種再沒有新發展的「古
董」。不過,當代某些學者運用「廣義量詞理論」或現代數學的某些方法,對古典形式邏輯研究的某些課題重
新進行研究,使這些課題重獲新生。舉例說,van Eijck、van Benthem、Westerstahl等人便從「廣義量詞理論
」的角度重新考察傳統的「三段論」推理,證明了一些結果。其他一些學者則致力推廣傳統的「三段論」概念
,以發掘新的「三段論」推理,例如Reichenbach提出包含「主詞否定」的「三段論」,Peterson把「三段論」
推廣至某些模糊量詞(如"almost all"、"most"、"many")以及表示數量、比例的量詞(他稱為「中間量詞」
Intermediate Quantifier),Ferdinando和Antonio則綜合前人的成果,發展出多種新的「三段論」(他們稱為
「特殊三段論」Distinctive Syllogism、「數值三段論」Numerical Syllogism、「模糊三段論」Fuzzy
Syllogism等)。
除了「三段論」推理外,「對當關係」推理在近年也有新的發展。周家發在《論自然語
言量化結構的單調推理關係》一文中,揭示了「古典對當方陣」背後的理據,總結出「對當方陣一般模式」
,從而發掘出自然語言中很多前人未曾發現的「對當關係」。Brown則從量詞邏輯關係的角度推導出4大類(下分
34小類)「對當方陣」,大大擴展了「對當方陣」的定義。有些學者則把「古典對當方陣」中的「矛盾關係」、
「(下)反對關係」和「差等關係」分別修改為「外部否定(Outer Negation)關係」(又稱「前補(Complement)關
係」)、「內部否定(Inner Negation)關係」(又稱「後補(Post-Complement)關係」和「對偶(Dual)關係」,並
以這些新關係構成「對當方陣」。這樣,繼前述的「古典對當方陣」和「布爾對當方陣」之後,我們又有第三
種對當方陣,姑名之為「新型對當方陣」:

請注意上圖中的關係並不等同於「古典對當方陣」中的關係(惟「外部否定關係」卻是例外,這種關係等同於「
古典對當方陣」中的「矛盾關係」),亦請注意上圖中「對偶關係」的雙箭頭,這有別於「古典對當方陣」中「
差等關係」的單箭頭。
順帶一提的是,當代有很多學者致力把傳統的「對當方陣」改造成其他幾何圖形,包括三角形、六角形、八角
形、立方體、十四面體,乃至更複雜的圖形,形成了邏輯學與幾何學的奇妙結合。2007年世界各地學者更舉行
「第一屆對當方陣世界大會」,總結了當代學者從不同角度對「對當方陣」的研究成果,證明了此一古老課題
在新世紀仍然具有巨大的魅力。
由於量詞與數學關係密切,很多研究「廣義量詞理論」的學者(尤其是數理邏輯基礎強的學者)很自然會傾向於
從數學或數理邏輯的角度研究量詞,因此當代「廣義量詞理論」的研究重點也包括某些與邏輯密切相關的課題
。由於這方面的研究涉及很強的技術性,有些研究結果的艱深程度可媲美當代的數學和邏輯學,所以這裡只能
提供很膚淺的介紹。
與「廣義量詞理論」有關的其中一個邏輯課題是研究如何用「廣義量詞」擴大「一階謂詞邏輯」推理系統。現
代數理邏輯主要以「一階謂詞邏輯」作為研究對象,可是這個推理系統只有兩個量詞,因此有些學者嘗試把某
些「廣義量詞」加入到「一階謂詞邏輯」中,看看能得到甚麼樣的推理系統,即擴大後的系統能推出甚麼結果
,以及這個系統滿足哪些「元邏輯性質」。當然,加入不同的「廣義量詞」會得到不同的推理系統,這些系統
的「公理化」(Axiomatization)問題、「證明論」(Proof Theory)問題以及系統之間的關係也是學者研究的課
題之一。
另一個廣受關注的課題是自然語言或邏輯語言對量詞的「表達力」(Expressive Power)問題,即是否能用這些
語言表達某些量詞的問題。前面說過,「一階謂詞邏輯」的「表達力」很弱(例如前面說過,用「一階謂詞邏輯
」的語言無法表達「偶數個」、「有限個」、「多數」等量詞),可是究竟弱到甚麼程度,這是值得研究的問題
。如同邏輯系統一樣,我們也可以透過把某些「廣義量詞」加入到「一階謂詞邏輯」的語言中,以加強其「表
達力」。由此可見,這個問題跟上段的問題很相似,但兩者畢竟是不同的概念,因此如何準確定義自然語言或
邏輯語言的「表達力」和「廣義量詞」的「可定義性」(Definability),以及「表達力」和「可定義性」與邏
輯推理之間的關係,這就不是一個簡單的問題。Peters和Westerstahl在Quantifiers in Language and
Logic一書中便用了超過四分一的篇幅專門討論這個課題,由此可見這個課題的重要性。
除了上述課題外,有些學者亦把「廣義量詞理論」與某些邏輯學分支(例如「模態邏輯」、「條件句邏輯」等)
、數學學科(例如「組合學」Combinatorics、「博奕論」Game Theory等)乃至電腦學學科(例如「自動機
Automaton理論」「計算複雜性Computational Complexity理論」等)的理論相結合,形成新的課題。筆者對這
些課題認識甚少,不能作詳盡的介紹。
除了「廣義量詞理論」外,當代「形式語義學」尚有其他研究量化問題的分支理論,也值得我們關注。有些理 論是由於研究某些個別的量化問題而產生的。舉例說,對於英語的「不定冠詞」"a(n)"的語義,從Russell以來 便把它理解成等同於「特稱量詞」。可是在以下的「驢子句」(Donkey Sentence)中,
兩個"a"的語義都必須理解為「全稱量詞」而非「特稱量詞」,即上句的「一階謂詞邏輯」表達式應為
上述這種問題驅使Kamp和Heim分別創立了「話語表現理論」(Discourse Representation Theory)和「文本更新
語義學」(File Change Semantics),有些人又把這兩套有共通性的理論合稱為「坎普-海姆理論」(Kamp-Heim
Theory)。不過,後來有些人認為「坎普-海姆理論」仍有缺陷,於是又發展出其他理論,例如Chierchia的「動
態約束理論」(Dynamic Binding Theory)以及Groenendijk和Stokhof的「動態謂詞邏輯」(Dynamic Predicate
Logic)。以上這些理論都可合稱為「動態語義學」(Dynamic Semantics),是當代「形式語義學」的另一個重要
分支。我們可以說,「動態語義學」是為了解決某些疑難的量化問題而產生的。
當代「形式語義學」的另一分支「類型-邏輯語義學」(Type-Logical Semantics)也相當重視量化問題,例如
Carpenter在其Type-Logical Semantics一書中便設計了多個量化算子,用來表達某些語義問題,例如
「反身代詞」(Reflexive Pronoun)、「相互代詞」(Reciprocal Pronoun)、「複數名詞短語」的「逐指解」
(Distributive Reading)和「統指解」(Collective Reading)等。
除了「形式語義學」外,當代「語用學」(Pragmatics)的某些理論也涉及量詞用法的解釋。舉例說,Grice的「
合作原則」(Cooperative Principle)便可用來解釋「特稱量詞」的「會話隱涵」(Conversational
Implicature)現象,即在日常會話中當我們說「有些學生及格」時,我們是隱含著「並非所有學生及格」的意
思(雖然在邏輯上「有些學生及格」與「所有學生及格」並不矛盾)。後來Horn更把這種涉及量詞或程度詞的「
會話隱涵」現象概括為他的「梯級隱涵」(Scalar Implicature)理論。
近年來某些學者的研究方向是研究如何把「語用學」形式化,以發展出一套能與「形式語義學」和「形式語法
學」鼎足而立的「形式語用學」(Formal Pragmatics)。Kadmon的Formal Pragmatics一書便是這方面的
嘗試,不過該書只著重介紹「坎普-海姆理論」以及有關「預設」和「焦點」的形式化理論。由Searle和
Vanderveken開創的「語力邏輯」(Illocutionary Logic)則是對「語用學」中Austin的「言語行為理論」
(Speech Act Theory)進行形式化的嘗試。後來蔡曙山將「語力邏輯」發展為完整的形式推理系統(蔡曙山將
"Illocutionary Logic"譯作「語用邏輯」),其中包括語力邏輯的量詞理論。
「語法學」也有研究量詞(本文所述的「量詞」主要對應於語法學上的「名詞短語」和「限定詞」)。儘管當代
的「生成語法」也很關注「多重量化句」(即含有多個量詞的句子)的「轄域歧義」(Scope Ambiguity)問題,並
因而提出「邏輯式」的概念,從而使「生成語法」研究在這方面與邏輯學研究有重合的地方;但語法學對量詞
的研究取向畢竟與「形式語義學」的研究取向很不相同,兩者的理論框架的重合地方不多。
不過在Fillmore、Kay和O'Connor開創的「構式語法」(Construction Grammar)框架下,有一個「梯級模型」
(Scalar Model)卻值得我們關注。「梯級模型」最初是Fillmore等人用來解釋英語的"even"(相當於漢語的「連
」)、"let alone"(相當於漢語的「更遑論」)等詞項的語義語用特點而設計的。這些詞項的共同特點是它們都
是「極性敏感詞」(Polarity Sensitive Item),即只能用於肯定或否定/疑問語境,用來加強或減弱語氣。後
來Israel在Polarity Sensitivity as Lexical Semantics一文中把「梯級模型」視為解釋所有「極性
敏感詞」的理論框架。雖然「極性敏感詞」不是量詞,但它們表達了某種程度和比較關係,可以說是表達了一
種抽象的「量」,而且其中一個「極性敏感詞」"any"(相當於漢語的「任何」)(註20)就常被看成具有「全稱量
詞」或「特稱量詞」的性質。筆者認為,「梯級模型」應有廣闊的應用前景。


