
在前面幾章,筆者介紹了量詞的多種性質,本章將繼續介紹量詞的其他重要性質。本章討論的量詞將以有限論
域下的「邏輯限定詞」為主,即滿足「右守恆性」、「擴展性」和「同構封閉性」(亦即「數量性」)的「有限
論域限定詞」。此外,為簡化討論,以下一般只考慮「局部限定詞」,即定義在同一論域U下的限定詞。我們把
由「邏輯限定詞」和「有限論域限定詞」組成的集合分別記作LOG和FIN。
由於限定詞可被看成表達兩個集合之間的關係,所以集合論中的各種二元關係也可以被看成限定詞的性質,本
文把這些性質統稱為「關係性質」(Relational Properties)。有關這些性質的討論,主要見於van Benthem的
Questions About Quantifiers、Zwarts的Determiners: A Relational Perspective和
Westerstahl的Some Results on Quantifiers,本章的主旨是綜合和擴充上述論文的成果。
在前面幾章,筆者曾指出「邏輯限定詞」的真值條件可以表現為集合函數Q(A)(B)和數字函數Q[x, y]這兩種形 式,其中A和B是Q的「集合論元」,x和y則是Q的「數字論元」,而且這兩類論元存在以下關係:x = |A − B|,y = |A ∩ B|。例如"every"的真值條件便可以表達為
對於「有限論域邏輯限定詞」而言,我們還可以把它們表現為「數字三角形」的形式,即由「+」號和 「−」號組成的三角形,三角形上的位置對應著下圖中的有序對:

請注意學者一般把「數字三角形」上的三個方向分別稱為「對角線」(Diagonal)、「行」(Row)和「列」
(Column)。利用「數字三角形」,我們可以很直觀地表達某些限定詞的真值條件,例如"every"在「數
字三角形」上便表現為,最右一「行」全為「+」號,其他位置全為「−」號。
「邏輯限定詞」的各種性質的定義也可以表現為集合和數字這兩種形式。Westerstahl指出,如果有關定義採取
「純全稱量化」(即除了「全稱量詞」外,不含其他量詞)的形式,那麼有一種機械的方法把該定義從集合形式
轉換為數字形式。假設有關定義的集合形式僅涉及兩個集合變項A和B,那麼我們可以利用x = |A − B|,
y = |A ∩ B|,z = |B − A|和u = |U − (A ∪ B)|以及前述「集合論元」與「數字論元」
的關係,把集合形式轉換為數字形式。舉例說,下文將會介紹的「連通性」的集合定義為
根據前述「集合論元」與「數字論元」的關係,以及A = B等價於A ⊆ B ∧ B ⊆ A,上述定義等 價於
把適當的x、y、z、u代入上式,便可得到「連通性」的數字定義(註1):
如果集合定義涉及三個集合變項,我們便要利用下圖:

舉例說,下文將會介紹的「傳遞性」的集合定義為
利用前述「集合論元」與「數字論元」的關係以及上圖,便可把上式改寫為
在「有限論域邏輯限定詞」中,有兩個具有特殊地位,分別是「恆真限定詞」(又稱「全集限定詞」,記作"1") 和「恆假限定詞」(又稱「空集限定詞」,記作"0"),在「數字三角形」上它們分別表現為全部取「+」號和全 部取「−」號。我們把這兩個限定詞的極端性質稱為「平凡性」(Triviality),以下記作TRIV ,即
設P為某種限定詞性質,一般而言,P可表達為條件句(包括「無條件句」,即沒有前提,只有結論的條件句), 我們可以把P看成由滿足該種性質的限定詞組成的集合。由於兩個「平凡限定詞」分別具有恆真和恆假的性質, 若P的結論具有Q(A)(B)的形式,必有1 ∈ P;若P的結論具有~Q(A)(B)的形式,則必有0 ∈ P。舉例 說,"1"和"0"便分別屬於以下這兩個自相矛盾的性質:
由此可見,「平凡限定詞」對於限定詞性質的研究沒有多大意義。為此我們引入「非平凡性」 (Non-Triviality)(記作~TRIV)的定義,即Q是「非平凡」的當且僅當
在「數字三角形」上,「非平凡限定詞」表現為:存在至少一個「+」號和至少一個「−」號。我們可以 把「非平凡性」看成對限定詞的一種最低要求,即限定詞不應在任何情況下都只取一個常值而毫無變化。某些 學者把這種要求加以推廣,從而得到「變異性」(Variety)(記作VAR)的概念,其定義為:Q是「變異」 的當且僅當
在「數字三角形」上,「變異限定詞」表現為:除了[0, 0]所在的「對角線」外,在每條「對角線」上,都有 至少一個「+」號和至少一個「−」號。容易看到,「變異性」是比「非平凡性」嚴格得多的要求,由此 我們有
在以下的討論中,我們將會看到「變異性」如何限制限定詞的可能範圍。
下表列出限定詞的各種「關係性質」的定義(註2):
| 名稱 | 代號 | 定義 |
|---|---|---|
請注意上表所列的各種「否」性質/「反」性質並非相關性質的矛盾概念。以「自反性」為例,以下列出其矛 盾概念以及「否自反性」的定義以作比較:
上述兩個定義顯然不是等價的。換句話說,一個限定詞若不是「自反」的,也不一定是「否自反」的,即存在
既非「自反」又非「否自反」的限定詞,例如"some"就是這樣的限定詞,因為一方面若A ≠ Φ,
我們有some(A)(A);另一方面亦有~some(Φ)(Φ)。
不過,我們可以把「否自反性」看成「自反性」的「外補性質」。「外補性質」的定義如下:設P、P'為限定詞
的某兩種性質,我們說P'是P的「外補性質」當且僅當對任何限定詞Q,均有
此外,我們說P是「自外補性質」當且僅當對任何限定詞Q,均有
根據上表的定義,容易得到以下定理:
| 定理1: | (i) REF與I-REF互為「外補性質」 |
| (ii) Q-REF與Q-UNI互為「外補性質」 | |
| (iii) W-REF與W-UNI互為「外補性質」 | |
| (iv) S-LIN與A-SYM互為「外補性質」 | |
| (v) AN-SYM與CONN互為「外補性質」 | |
| (vi) TRANS與AL-CONN互為「外補性質」 | |
| (vii) SYM為「自外補性質」 |
以下僅證(vi)以作示範。先證Q ∈ TRANS ⇒ ~Q ∈ AL-CONN,故設Q ∈ TRANS,那麼對所有 A、B、C,有
| (Q(A)(B) ∧ Q(B)(C)) ⇒ Q(A)(C) | |
| ≡ | ~Q(A)(C) ⇒ ~(Q(A)(B) ∧ Q(B)(C)) |
| ≡ | ~Q(A)(C) ⇒ (~Q(A)(B) ∨ ~Q(B)(C)) |
即~Q ∈ AL-CONN。同理,易證Q ∈ AL-CONN ⇒ ~Q ∈ TRANS。
表1提供了各種限定詞性質的標準定義。可是,在「有限論域」和「邏輯性」的假設下,這些定義往往可以得到 簡化,或者變得較便於操作,以下定理提供表1中六種性質的新定義(註3):
| 定理2: | 在LOG ∩ FIN下, |
| (i) Q ∈ REF當且僅當A ⊆ B ⇒ Q(A)(B),即x = 0 ⇒ Q[x, y] | |
| (ii) Q ∈ I-REF當且僅當Q(A)(B) ⇒ A ~⊆ B,即Q[x, y] ⇒ x ≠ 0 | |
| (iii) Q ∈ AN-SYM當且僅當Q(A)(B) ⇒ A ⊆ B,即Q[x, y] ⇒ x = 0 | |
| (iv) Q ∈ CONN當且僅當A ~⊆ B ⇒ Q(A)(B),即x ≠ 0 ⇒ Q[x, y] | |
| (v) Q ∈ SYM當且僅當Q(A)(B) ⇔ Q(A ∩ B)(A ∩ B),即Q[x, y] ⇔ Q[0, y] | |
| (vi) Q ∈ AN-EUCLID當且僅當Q(A)(B) ⇔ Q(A)(A),即Q[x, y] ⇔ Q[0, x + y] |
請注意上述定理同時提供了集合形式和數字形式,而後者是用2.1小節介紹的方法從前者轉換而來的。因此在證
明上述定理的各部分時,我們可以選擇證明其集合形式或數字形式,視乎哪一種方式較為方便。對於(i),筆者
選擇證明其集合形式。在以下證明中,我們假設A、B為任意集合。首先設Q ∈ REF,並且A ⊆ B。根
據表1中「自反性」的定義,有Q(A)(A)。由A ⊆ B得A = A ∩ B,故有Q(A)(A ∩ B)。根據「右守
恆性」,有Q(A)(B)。由此證得若Q ∈ REF,則A ⊆ B ⇒ Q(A)(B)。
其次設A ⊆ B ⇒ Q(A)(B)成立,那麼由於A ⊆ A,必有Q(A)(A),即Q ∈ REF。由此證得若A
⊆ B ⇒ Q(A)(B),則Q ∈ REF。綜合以上結果,(1)得證。請注意由於I-REF是REF的「外補性質」
(定理1(i)),從(i)可得Q ∈ I-REF當且僅當~Q ∈ REF,當且僅當A ⊆ B ⇒ ~Q(A)(B),即
Q(A)(B) ⇒ A ~⊆ B,故(ii)得證。
對於(iii),筆者選擇證明其數字形式,為此須先把表1中「反對稱性」的定義轉換為數字形式,即
首先設Q ∈ AN-SYM,即(5)成立,並設Q[x, y],由於Q[x, y]等價於Q[x, y] ∧ Q[x, y],從(5)馬上
推得x = 0,由此證得若Q ∈ AN-SYM,則Q[x, y] ⇒ x = 0。
其次設Q[x, y] ⇒ x = 0,那麼從Q[x, y] ∧ Q[z, y]可馬上推得x = 0 ∧ z = 0,由此證得若
Q[x, y] ⇒ x = 0,則(5)成立,即Q ∈ AN-SYM。綜合以上結果,(iii)得證。請注意由於CONN是
AN-SYM的「外補性質」(定理1(v)),從(iii)可得Q ∈ CONN當且僅當~Q[x, y] ⇒ x = 0,即x ≠ 0
⇒ Q[x, y],故(iv)得證。
接著考慮(v),根據《廣義量詞系列:量詞的代數性質》的「定理12(i)」
,在「右守恆性」的條件下,SYM等價於INT;而《廣義量詞系列:單調性的進
階研究》的「定理2」已證明了Q ∈ INT當且僅當Q(A)(B) ⇔ Q(A ∩ B)(A ∩ B)。綜合以
上結果,(v)的集合形式得證。
最後考慮(vi),筆者選擇證明其數字形式,為此須先把「反歐幾里德性」的定義轉換為數字形式,即
首先設Q ∈ AN-EUCLID,即(6)成立。由於(6)對任何非負整數均成立,我們可以把適當的整數代入(6)從而 得到我們需要的結果。把x2 = x4 = x6 = x7 = 0, x3 = x和x1 = y代入(6),得
同理,把x3 = x4 = x7 = 0,x2 = x6 = x, x1 = y代入(6),得
綜合以上結果,證得若Q ∈ AN-EUCLID,則Q[x, y] ⇔ Q[0, x + y]。
其次假設Q[x, y] ⇔ Q[0, x + y]成立。設Q[x3 + x4, x1 +
x2],從上述假設可推得Q[0, x1 + x2 + x3 +
x4]。由此再次根據上述假設,又可推得Q[x2 + x4, x1 +
x3],即(6)成立。由此證得若Q[x, y] ⇔ Q[0, x + y],則Q ∈ AN-EUCLID。綜合以上結
果,(vi)得證。
接著我們從「數字三角形」的角度理解上述定理。(i)是說,「自反限定詞」的「數字三角形」上最右一「行」
全為「+」號(此外其他位置亦可能有「+」號)。(ii)是說,「否自反限定詞」的「數字三角形」上最右一「行」
全為「−」號(此外其他位置亦可能有「−」號)。(iii)是說,「反對稱限定詞」的「數字三角形」
上最右一「行」以外各「行」全為「−」號(此外最右一「行」上亦可能有「−」號)。(iv)是說,
「連通限定詞」的「數字三角形」上最右一「行」以外各「行」全為「+」號(此外最右一「行」上亦可能有「+
」號)。下圖顯示上述四種性質的「數字三角形」特徵:
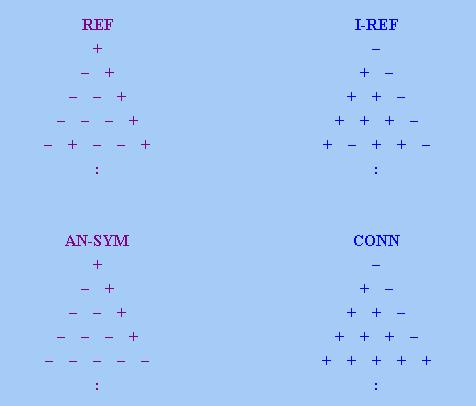
至於其餘兩點,(v)是說,「對稱限定詞」的「數字三角形」上每「列」要麼全為「+」號,要麼全為「− 」號。(vi)是說,「反歐幾里德限定詞」的「數字三角形」上每條「對角線」要麼全為「+」號,要麼全為「 −」號。請注意此一結果跟《廣義量詞系列:單調性的進階研究》 5.3小節中的圖完全吻合(請記著在本文中,SYM等價於INT)。由此也證明了,本文對「反歐幾里德性」的定義跟 上述網頁的定義等價。下圖顯示上述兩種性質的「數字三角形」特徵:

在眾多「關係性質」中,「傳遞性」和「近連通性」最為特殊,因為它們可以表述為特別的形式,詳見以下定 理:
| 定理3: | 在LOG ∩ FIN下, | |
| (i) | 若Q ∈ TRANS,則Q(A)(B) ⇒ (A ⊆ B ∨ Q(A)(Φ)), 即Q[x, y] ⇒ (x = 0 ∨ Q[x + y, 0]) | |
| (ii) | 若Q ∈ TRANS,則Q(A)(Φ) ⇒ Q(A)(B),即Q[x + y, 0] ⇒ Q[x, y] | |
| (iii) | 若Q ∈ TRANS,則(Q(A)(A) ∧ Q(C)(D) ∧ C
~⊆ D ∧ |C| > |A|) ⇒ Q(A)(B), 即(Q[0, x + y] ∧ Q[v, w] ∧ v ≠ 0 ∧ v + w > x + y) ⇒ Q[x, y] |
|
| (iv) | Q ∈ TRANS當且僅當存在兩個由非負整數組成的集合S和T
,使得S < T,並且 Q(A)(B) ⇔ |A| ∈ S ∨ (A ⊆ B ∧ |A| ∈ T), 即Q[x, y] ⇔ x + y ∈ S ∨ (x = 0 ∧ x + y ∈ T) |
|
| (v) | Q ∈ AL-CONN當且僅當存在兩個由非負整數組成的集合S和T
,使得S < T,並且 Q(A)(B) ⇔ |A| ∈ ~(S ∪ T) ∨ (A ~⊆ B ∧ |A| ∈ T), 即Q[x, y] ⇔ x + y ∈ ~(S ∪ T) ∨ (x ≠ 0 ∧ x + y ∈ T) |
|
在上述定理中,S和T可以為空集,S < T代表S中所有元素均小於T中所有元素。請注意在上述定理中,(iv)和 (v)才是我們最終想得到的結果,(i)-(iii)可以被看成(iv)的「引理」。現在讓我們證明上述定理,以下將主 要採用上述定理的數字形式。為此首先把「傳遞性」的定義轉換為數字形式,即
把x2 = x6 = 1,x3 = 0,x5 = x,x1 = y, x4 = x + 1代入(7),得
從上式可以推得
我們可以重覆運用上式,直至Q的第二論元變成0為止,因此從上式又可推得
(i)至此得證。
接著考慮(ii),把x1 = x2 = x6 = 0,x4 = x,
x3 = y,x5 = x + y代入(7),得
(ii)乃得證。
接著考慮(iii),設Q[0, x + y] ∧ Q[v, w] ∧ v ≠ 0 ∧ v + w > x + y。取v' = x,w' = v +
w − x,那麼我們有v' ≥ x、w' ≥ y並且v + w = v' + w'。根據(i),我們可以從Q[v, w]推出
Q[v + w, 0],即Q[v' + w', 0]。由此根據(ii),可以推出Q[v', w']。現在如果我們把x3 =
x4 = 0、x2 = x,x1 = y,x5 = v' − x,
x6 = w' − y代入(7),便可得到
由於我們在前面假設Q[0, x + y],並已證明了Q[v', w'],從上式可推出Q[x, y],至此(iii)乃得證。
接著證明(iv),首先設Q ∈ TRANS。設S = {x: Q[x, 0]},T = {y: S < {y} ∧ Q[0, y]},那麼S中所
有元素都少於T中所有元素。接著讓我們證明S和T具有(iv)中所述的性質,若x + y ∈ S,即Q[x + y, 0]
,那麼根據(ii),有Q[x, y];若x = 0 ∧ x + y = y ∈ T,那麼根據T的定義,亦有Q[x, y]。至此證
明了x + y ∈ S ∨ (x = 0 ∧ y ∈ T) ⇒ Q[x, y]。接著設Q[x, y],這時有兩種可能情
況。第一種情況是x ≠ 0,由此根據(i),有Q[x + y, 0],即x + y ∈ S。第二種情況是x = 0,這時又
有兩種子情況,第一種子情況是S < {y},由此根據T的定義,有x + y = y ∈ T。第二種子情況是S ~<
{y},即存在z ∈ S使得z ≥ y。若z = y,則有y ∈ S,亦即x + y ∈ S;若z > y,則我們有
由此根據(iii),有Q[y, 0]。根據S的定義,有y ∈ S,亦即x + y ∈ S。至此證明了Q[x, y] ⇒
x + y ∈ S ∨ (x = 0 ∧ x + y ∈ T)。綜合以上情況,我們證明了以上定義的S和T的確具有
(iv)中所述的性質。
其次,我們使用(iv)的集合形式來證明,若存在(iv)中所述的集合S和T,滿足S < T並且
則Q ∈ TRANS。為此,設Q(A)(B) ∧ Q(B)(C)。現在有兩種可能情況,第一種情況是|A| ∈ S,由
此根據上式,有Q(A)(C)。第二種情況是A ⊆ B ∧ |A| ∈ T,由於|A| ≤ |B|,所以|B|
~∈ S,故必有B ⊆ C ∧ |B| ∈ T。由此推得A ⊆ C ∧ |A| ∈ T,即Q(A)(C)
。至此證得Q(A)(B) ∧ Q(B)(C) ⇒ Q(A)(C),即Q ∈ TRANS。綜合以上情況,(iv)得證。
最後考慮(v),根據「定理1(vi)」,Q ∈ AL-CONN ⇔ ~Q ∈ TRANS,而根據(iv),~Q(A)(B)當且
僅當
| ~(x + y ∈ S ∨ (x = 0 ∧ x + y ∈ T)) | |
| ⇔ | x + y ~∈ S ∧ ~(x = 0 ∧ x + y ∈ T) |
| ⇔ | x + y ~∈ S ∧ (x ≠ 0 ∨ x + y ~∈ T) |
| ⇔ | x + y ~∈ S ∧ ((x ≠ 0 ∧ x + y ∈ T) ∨ x + y ~∈ T) |
| ⇔ | (x + y ~∈ S ∧ x ≠ 0 ∧ x + y ∈ T) ∨ (x + y ~∈ S ∧ x + y ~∈ T) |
| ⇔ | (x + y ∈ T ∧ x ≠ 0) ∨ x + y ∈ ~(S ∪ T) |
(v)乃得證。
現在讓我們看(iv)和(v)分別為我們提供甚麼樣的限定詞。首先,把S = {0},T = {1, 2, ...}代入(iv)和(v)
中的集合條件,所得限定詞分別為
Q和Q'分別是"every"和"(not every)",容易驗證前者滿足「傳遞性」,後者滿足「近連通性」 。其次,把S = {3},T = {5, 6, ...}代入(iv)和(v)中的條件,所得限定詞分別為
上述兩個限定詞似乎可以用自然語言分別表達為"(some or none of 3; or all of 5 or more)"和 "(some or none of 0 or 1 or 2 or 4; or not all of 5 or more)"。一般地,任意「傳遞限定詞」 均可表達為
其中s1, ... sm ∈ S,t1, ... tn∈ T,並且S < T。類似地,任意「近連通限定詞」均可表達為
其中s1, ... sm ∈ ~(S ∪ T),t1, ... tn ∈
T,並且S < T (註4)。
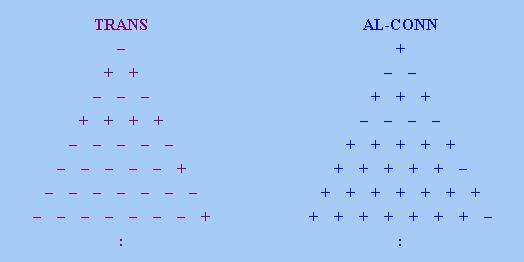
從「數字三角形」的角度看,根據(iv),「傳遞限定詞」的「數字三角形」分為上下兩部分,上半部的每條「
對角線」要麼全是「+」號,要麼全是「−」號;而下半部的每條「對角線」要麼全是「−」號,要
麼只有最右的位置取「+」號。類似地,「近連通限定詞」的「數字三角形」也分為上下兩部分,上半部的每條
「對角線」要麼全是「+」號,要麼全是「−」號;而下半部的每條「對角線」要麼全是「+」號,要麼只
有最右的位置取「−」號。下圖顯示「傳遞限定詞」和「近連通限定詞」的「數字三角形」特徵:
利用上述定義和結果,我們可以推導出與「關係性質」有關的一系列定理。為方便以下某些定理的證明,我們
首先引入以下定理:
定理4:

上圖中的x和y代表所在子集的基數。根據A'的定義,我們有Q(A)(A ∩ A')。從而根據「右守恆性」,有
Q(A)(A')。由於|A ∩ A'| = |A' ∩ A| = y並且|A − A'| = |A' − A| = x,根據「邏
輯性」,我們可以從Q(A)(A')推出Q(A')(A)。
以下定理表達某些「關係性質」之間的包含關係:
| 定理5: | 在LOG ∩ FIN下, |
| (i) REF ⊆ W-REF ⊆ Q-REF | |
| (ii) I-REF ⊆ W-UNI ⊆ Q-UNI | |
| (iii) AN-SYM ⊆ TRANS ⊆ Q-REF | |
| (iv) CONN ⊆ AL-CONN ⊆ Q-UNI | |
| (v) SYM ⊆ W-SYM |
以下證明上述定理。(i)和(ii)的前半部可以從表1的集合定義直接推得。設Q ∈ REF,那麼對任何B都有
Q(B)(B)。而W-REF的定義比REF的定義弱,因此如果有Q(A)(B),自然便有Q(B)(B),即Q ∈ W-REF,故有
REF ⊆ W-REF。同理,根據I-REF的定義以及W-UNI定義的逆否命題,容易證得I-REF ⊆ W-UNI。
(i)和(ii)的後半部可以從數字三角形的角度推得。根據表1,W-REF、Q-REF、W-UNI和Q-UNI的數字定義分別為
從「數字三角形」去理解,(8)的意思是,「弱自反限定詞」的「數字三角形」上某位置[x, y]若取「+」號, 則最右一「行」的[0, y]及其右下全部位置都取「+」號。(9)的意思是,「準自反限定詞」的「數字三角形」 上某位置[x, y]若取「+」號,則[x, y]所在的「對角線」上最右面的位置也取「+」號。(10)的意思是,「弱 全集限定詞」的「數字三角形」最右一「行」上某位置[0, w]若取「+」號,則[0, w]所在的整「列」以及其左 上方的所有「列」都取「+」號(此外其他「行」上的某些位置亦可能取「+」號)。(11)的意思是,「準全集限 定詞」的「數字三角形」最右一「行」某位置[0, w]若取「+」號,那麼[0, w]所在的整條「對角線」都取「+」 號(此外其他「行」上的某些位置亦可能取「+」號)。下圖顯示上述四種性質的「數字三角形」特徵:

按照上述理解,容易看到(8) ⇒ (9)並且(10) ⇒ (11),由此證得W-REF ⊆ Q-REF和W-UNI
⊆ Q-UNI。綜合以上結果,(i)和(ii)得證。
接著考慮(iii)。首先設Q ∈ AN-SYM,並設Q(A)(B) ∧ Q(B)(C),那麼根據「定理2(iii)」,有A
⊆ B ∧ B ⊆ C。由此得A ⊆ C。另外,根據「右守恆性」,我們可以從Q(A)(B)推得Q(A)(A
∩ B),由此得Q(A)(A)(因為A ⊆ B ⇔ A ∩ B = A),並由此得Q(A)(A ∩ C)(因為A
⊆ C ⇔ A ∩ C = A)。最後,根據「右守恆性」,可以推得Q(A)(C)。至此證得(Q(A)(B) ∧
Q(B)(C)) ⇒ Q(A)(C),即Q ∈ TRANS。
其次設Q ∈ TRANS,並設Q(A)(B)。根據「定理4」,存在集合A'使得Q(A)(A') ∧ Q(A')(A)。根據「傳
遞性」,我們可以從Q(A)(A')和Q(A')(A)推出Q(A)(A)。至此證明了Q(A)(B) ⇒ Q(A)(A),即Q ∈
Q-REF。綜合以上結果,(iii)得證。
接著考慮(iv)。首先設Q ∈ CONN,那麼根據「定理1(v)」,~Q ∈ AN-SYM。由此根據(iii),有~Q
∈ TRANS。再根據「定理1(vi)」,Q ∈ AL-CONN。利用類似方法,亦可證得Q ∈ AL-CONN
⇒ Q ∈ Q-UNI,(iv)乃得證。
最後,(v)可以從表1的集合定義直接推得,設Q ∈ SYM,那麼對任何A、B都有Q(A)(B) ⇒ Q(B)(A)。
而W-SYM的定義比SYM的定義弱,因此如有Q(A)(B) ∧ Q(B)(C),就自然有Q(B)(A),即Q ∈ W-SYM,由
此證得(v)。
利用前述的定義和定理,我們還可以推導出一些否定性結果。首先,表1所列的某些性質在LOG ∩ FIN − TRIV的條件下並無實例,請看以下定理:
| 定理6: | 在LOG ∩ FIN − TRIV下, |
| (i) S-LIN = Φ | |
| (ii) A-SYM = Φ | |
| (iii) EUCLID = Φ | |
| (iv) CIRC = Φ |
為證明(i),首先寫出S-LIN的數字定義如下:
設有Q ∈ S-LIN,並設x、y為任意非負整數,把x代入z,上式便等價於Q[x, y],即對任意非負整數Q[x,
y]均成立,但這違反「非平凡性」,所以S-LIN = Φ。從(i)可以馬上證得(ii),這是因為如果有Q ∈
A-SYM,那麼根據「定理1(iv)」,必有~Q ∈ S-LIN,但這與(i)矛盾,所以A-SYM = Φ。
接著證明(iii),首先寫出EUCLID的數字定義如下:
把x2 = x3 = x5 = 0,x4 = x,x1 = y, x6 = z代入(13),得
把x2 = x3 = x4 = x6 = 0,x1 = x5 = u代入(13),得
把x1 = x4 = x5 = x6 = 0,x2 = x3 = u代入(13),得
接著把y = z = 0,x = u代入(14),得
最後把x1 = x2 = x3 = x4 = 0,x5 = v, x6 = w代入(13),得
可是,根據(14),如果Q[x, y],那麼可以推出Q[0, u],其中u ≥ y。由此根據(15)-(17),可以推出Q[0,
0]。最後根據(18),可以推出Q[v, w]。由於x、y、v、w為任意非負整數,這即是說,Q的「數字三角形」要麼
全為「+」號,要麼全為「−」號,這違反「非平凡性」,所以不可能有Q ∈ EUCLID,(iii)得證。
最後使用CIRC的集合定義證明(iv),為此設有Q ∈ CIRC,並設Q(A)(B) ∧ Q(A)(C)。根據「定理4」,
存在集合A'使得Q(A)(A') ∧ Q(A')(A)。根據「循環性」,我們可以從Q(A)(A')和Q(A')(A)推出Q(A)(A)。
由此根據「循環性」和Q(A)(C)推得Q(C)(A)。由此再根據「循環性」和Q(A)(B)推得Q(B)(C)。至此證明了
(Q(A)(B) ∧ Q(A)(C)) ⇒ Q(B)(C),即Q ∈ EUCLID。但根據(iii),EUCLID = Φ,所以不可
能有Q ∈ CIRC,(iv)乃得證。
除了上述四種性質表現為空集外,某些性質的交集也表現為空集,請看以下定理:
| 定理7: | 在LOG ∩ FIN − TRIV下, |
| (i) REF ∩ AL-CONN = Φ | |
| (ii) I-REF ∩ TRANS = Φ | |
| (iii) REF ∩ CONN = Φ | |
| (iv) I-REF ∩ AN-SYM = Φ | |
| (v) W-REF ∩ CONN = Φ | |
| (vi) W-UNI ∩ AN-SYM = Φ | |
| (vii) SYM ∩ TRANS = Φ | |
| (viii) SYM ∩ AL-CONN = Φ | |
| (ix) SYM ∩ REF = Φ | |
| (x) SYM ∩ I-REF = Φ | |
| (xi) REF ∩ I-REF = Φ | |
| (xii) AN-SYM ∩ CONN = Φ |
以下證明上述定理。首先考慮(i),設有Q ∈ REF ∩ AL-CONN。根據「定理5(iv)」,Q ∈ Q-UNI
。根據REF的定義,對任何A都有Q(A)(A)。由此根據Q-UNI的定義,對任何A、B,都有Q(A)(B),違反「非平凡性
」,由此可知不存在Q ∈ REF ∩ AL-CONN,(i)乃得證。從(i)容易推出(ii),這是因為如果有Q
∈ I-REF ∩ TRANS,那麼根據「定理1(i)和(vi)」,必有~Q ∈ REF ∩ AL-CONN,但這與(i)
矛盾,(ii)乃得證。
利用(i)、(ii)以及「定理5(iv)和(iii)」,容易證得(iii)及(iv)。但我們可以從另一角度去證明,方法是證
明根據有關性質的集合定義,
首先證明(19),設Q ∈ S-LIN,那麼根據表1,容易看到Q ∈ CONN。此外,只要把A代入S-LIN定義中
的B,便可得到Q(A)(A),即Q ∈ REF,由此證得S-LIN ⊆ REF ∩ CONN。其次設Q ∈ REF
∩ CONN,我們考慮兩種情況。若A = B,那麼根據REF的定義,必有Q(A)(A),即Q(A)(B) ∨ Q(B)(A)。若
A ≠ B,那麼根據CONN的定義,必有Q(A)(B) ∨ Q(B)(A),因此Q ∈ S-LIN。綜合以上結果,(19)乃
得證。
(20)可以證明如下:
| Q ∈ A-SYM | ⇔ ~Q ∈ S-LIN | (根據「定理1(iv)」) |
| ⇔ ~Q ∈ REF ∩ CONN | (根據(19)) | |
| ⇔ Q ∈ I-REF ∩ AN-SYM | (根據「定理1(i)和(v)」) |
證明了(19)和(20)後,根據「定理6(i)和(ii)」,(iii)和(iv)得證。
接著我們從「數字三角形」的角度證明(v),設有Q ∈ W-REF ∩ CONN。根據3.2小節對CONN的「數字
三角形」的描述,Q的「數字三角形」上最右一「行」以外的各「行」全為「+」號。另外,根據4.1小節對W-REF
的「數字三角形」的描述,Q的「數字三角形」上某位置[x, y]若取「+」號,則最右一「行」的[0, y]及其右
下全部位置都取「+」號。結合前面的討論,必有整個「數字三角形」都是「+」號,違反「非平凡性」,由此可
知不存在Q ∈ W-REF ∩ CONN,(v)乃得證。從(v)以及「定理1(iii)和(v)」,容易推得(vi)。
接著考慮(vii),設有Q ∈ SYM ∩ TRANS,根據TRANS和SYM的集合定義,容易推得(Q(A)(B) ∧
Q(B)(C)) ⇒ Q(C)(A),即Q ∈ CIRC,但這與「定理6(iv)」矛盾,所以不存在Q ∈ SYM ∩
TRANS,(vii)乃得證。從(vii)以及「定理1(vi)和(vii)」,容易推得(viii)。
接著我們從「數字三角形」的角度證明(ix),設有Q ∈ SYM ∩ REF。根據「定理2(i)」,Q的「數字三
角形」上所有[0, y]位置都取「+」號。由此根據「定理2(v)」,所有[x, y]位置都取「+」號,違反「非平凡
性」,由此可知不存在Q ∈ SYM ∩ REF,(ix)乃得證。從(ix)以及「定理1(i)和(vii)」,容易推得
(x)。
(xi)可以根據REF和I-REF的集合定義直接推得,由於REF和I-REF的集合定義不可能同真,所以不可能有Q
∈ REF ∩ I-REF。
最後,設有Q ∈ AN-SYM ∩ CONN,那麼根據「定理2(iv)和(iii)」,可以推出x ≠ 0 ⇒ x =
0,此一矛盾說明不存在Q ∈ AN-SYM ∩ CONN,(xii)乃得證。
以上的定理都假設限定詞具有「非平凡性」,現在如果把「非平凡性」改為更嚴格的「變異性」,我們將有更
多否定性結果,以下僅提供兩個簡單的結果:
| 定理8: | 在LOG ∩ FIN ∩ VAR下, |
| (i) AN-EUCLID = Φ | |
| (ii) Q-REF ∩ Q-UNI = Φ |
我們從「數字三角形」的角度證明上述定理。首先考慮(i),設有Q ∈ AN-EUCLID。根據3.2小節對
AN-EUCLID的「數字三角形」的描述,Q的「數字三角形」的每條「對角線」要麼全為「+」號,要麼全為「
−」號,但這與「變異限定詞」的「數字三角形」特徵相悖,(i)乃得證。
其次考慮(ii),設有Q ∈ Q-REF ∩ Q-UNI。根據Q-REF和Q-UNI的數字定義(9)和(11),我們有
Q[x, y] ⇔ Q[0, x + y]。但根據「定理2(vi)」,這正是AN-EUCLID的數字定義,即在LOG ∩
FIN − TRIV下,
由此從(i)可馬上推出(ii)。
某些限定詞可以被表述為某些關係性質的交集,請看以下定理(在以下各點中,n為非負整數):
| 定理9: | 在LOG ∩ FIN − TRIV下, |
| (i) REF ∩ AN-SYM = {every} | |
| (ii) I-REF ∩ CONN = {(not every)} | |
| (iii) REF ∩ TRANS = ∪n ≥ 0{(some or none of n or fewer; or all of n + 1 or more)} | |
| (iv) I-REF ∩ AL-CONN = ∪n ≥ 0{(not all of n or more)} | |
| (v) W-REF ∩ SYM = {some, (at least 2), (at least 3) ...} | |
| (vi) W-UNI ∩ SYM = {no, (at most 1), (at most 2) ...} | |
| (vii) W-SYM ∩ AN-SYM = ∪n ≥ 0{(all of n)} | |
| (viii) W-SYM ∩ CONN = {(some or none of 1 or more)} |
首先證明(i)和(ii),設Q ∈ REF ∩ AN-SYM,根據「定理2(i)和(iii)」,Q(A)(B) ⇔ x = 0,即
Q的「數字三角形」上最右一「行」全為「+」號,其他位置全為「−」號,但這正是"every"的「
數字三角形」,(i)乃得證。根據「定理1(i)和(v)」以及~every = (not every),我們可以從
(i)直接推出(ii)。
接著證明(iii)和(iv),根據3.2和3.3小節對REF和TRANS的「數字三角形」的描述,Q ∈ REF ∩ TRANS
當且僅當其「數字三角形」分為上下兩部分,上半部的每條「對角線」全是「+」號,而下半部的每條「對角線
」只有最右的位置取「+」號,即S = {0, ... n},T = {n + 1, ...}。具有上述特徵的Q就是"(some or
none of n or fewer; or all of n + 1 or more)"。由於任何非負整數n均可滿足上述條件且不違反「非
平凡性」,(iii)乃得證。
根據「定理1(i)和(vi)」,Q ∈ I-REF ∩ AL-CONN當且僅當~Q ∈ REF ∩ TRANS,當且僅當Q
的「數字三角形」分為上下兩部分,上半部的每條「對角線」全是「−」號,而下半部的每條「對角線」
只有最右的位置取「−」號,即S = {0, ... n − 1},T = {n, ...}。由於~(S ∪ T) = Φ
,具有上述特徵的Q就是"(not all of n or more)"。由於任何非負整數n均可滿足上述條件且不違反「
非平凡性」,(iv)乃得證。
接著證明(v)和(vi),根據3.2和4.1小節對SYM和W-REF的「數字三角形」的描述,Q ∈ W-REF ∩ SYM且
不違反「非平凡性」,當且僅當其「數字三角形」有一條從右上到左下的「分界線」,在該「分界線」左上方
各「列」均取「−」號,右下方各「列」均取「+」號。具有上述特徵的Q就是"some"或"(at
least n)" (其中n ≥ 2),(v)乃得證。根據「定理1(iii)和(vii)」以及~some = no和
~(at least n) = (at most n − 1),我們可以從(v)直接推得(vi)。
為證明(vii)和(viii),我們首先推導W-SYM的一個只涉及數字變項x、y、z、w的數字定義。根據表1,W-SYM的
集合定義涉及Q(A)(B)、Q(B)(C)和Q(B)(A),其中Q(A)(B)和Q(B)(A)可分別表達為Q[x, y]和Q[z, y]。此外,由
於|B| = |B − A| + |B ∩ A| = |B − C| + |B ∩ C|,如果我們把|B ∩ C|寫成w,便
可以把Q(B)(C)表達為Q[y + z − w, w]。由此可得W-SYM的數字定義如下:Q ∈ W-SYM當且僅當對任
意非負整數x、y、z以及w ≤ y + z,均有
根據上式,Q ∈ W-SYM當且僅當其「數字三角形」上若有兩點取「+」號,只要該兩點不在同一「列」或同 一條「對角線」上,那麼其中一點所在「列」以及另一點所在「對角線」的交點也取「+」號(如果該交點在「 數字三角形」上的話)。下圖顯示W-REF的「數字三角形」特徵:

接著證明(vii),根據3.2小節以及上面對AN-SYM和W-SYM的「數字三角形」的描述,Q ∈ W-SYM ∩
AN-SYM且不違反「非平凡性」,當且僅當其「數字三角形」的最右一「行」上剛好有一點取「+」號,而「數字
三角形」的其餘部分則全為「−」號。具有上述特徵的Q就是(all of n)" (其中n ≥ 0),
(vii)乃得證。
最後證明(viii),根據3.2小節以及上面對CONN和W-SYM的「數字三角形」的描述,Q ∈ W-SYM ∩
CONN且不違反「非平凡性」,當且僅當其「數字三角形」只有唯一一個位置[0, 0]取「−」號。具有上述
特徵的Q就是"(some or none of 1 or more)"。
請注意如果我們把上述定理中的~TRIV改為VAR,(i)和(ii)不受影響,這是因為"every"和"(not
every)"符合VAR的定義。其餘各點中的限定詞則大幅減少,為證明這一點,我們首先引入以下定理:
| 定理10: | 在LOG ∩ FIN ∩ VAR下, |
| (i) AN-SYM = TRANS | |
| (ii) CONN = AL-CONN |
我們從「數字三角形」的角度證明(i),由於根據「定理5(iii)」,AN-SYM ⊆ TRANS,所以我們只需證明
TRANS ⊆ AN-SYM。設Q ∈ TRANS,根據3.3小節對TRANS的「數字三角形」的描述,如果S不等於Φ
和{0},那麼Q的「數字三角形」上除了[0, 0]外,還有某些「對角線」全為「+」號,違反「變異性」,因此必
有S等於Φ或{0},即Q的「數字三角形」只有最右一「行」有「+」號,但這正是AN-SYM的「數字三角形」特
徵,由此證得TRANS ⊆ AN-SYM,(i)乃得證。
接著證明(ii),由於根據「定理5(iv)」,CONN ⊆ AL-CONN,所以我們只需證明AL-CONN ⊆ CONN。設
Q ∈ AL-CONN,那麼根據「定理1(vi)」,~Q ∈ TRANS。根據(i),~Q ∈ AN-SYM。再根據「定理
1(v)」,Q ∈ CONN。由此證得AL-CONN ⊆ CONN,(ii)乃得證。
接著我們有以下定理:
| 定理11: | 在LOG ∩ FIN ∩ VAR下, |
| (i) REF ∩ TRANS = {every} | |
| (ii) I-REF ∩ AL-CONN = {(not every)} | |
| (iii) W-REF ∩ SYM = {some} | |
| (iv) W-UNI ∩ SYM = {no} | |
| (v) W-SYM ∩ AN-SYM = Φ | |
| (vi) W-SYM ∩ CONN = Φ |
本定理可從「定理9」推得。首先(i)可以從「定理9(i)」和「定理10(i)」直接推得。同理,(ii)也可以從「定
理9(ii)」和「定理10(ii)」直接推得。
其次考慮(iii),設Q ∈ W-REF ∩ SYM。在「定理9(v)」的結果中,若Q = (at least n)(其中
n ≥ 2),那麼Q的「數字三角形」的靠左面n「列」全為「−」號,這亦意味著首n條「對角線」全為「
−」號,違反「變異性」,因此Q只能是"some",(iii)乃得證。根據「定理1(iii)和(vii)」以及
~some = no,(iv)亦得證。
接著考慮(v),設有Q ∈ W-SYM ∩ AN-SYM。根據「定理9(vii)」,Q的「數字三角形」只有最右一「行
」上某個位置取「+」號,其餘的位置全為「−」號。但這顯然違反「變異性」,因此不存在這樣的Q,
(v)乃得證。
最後,根據「定理9(viii)」,Q ∈ W-SYM ∩ CONN當且僅當Q = (some or none of 1 or
more),但這個限定詞顯然違反「變異性」,(vi)乃得證。
現把以上提到的各個定理總結成下圖:

請注意為簡化上圖,上圖以LOG ∩ FIN ∩ VAR作為論域。上圖並不包括S-LIN、A-SYM、EUCLID、CIRC和 AN-EUCLID,這是因為這五種性質在上述論域下等於空集。此外,從上圖還可以容易推導出上文沒有提出的結果 ,例如在LOG ∩ FIN ∩ VAR下,TRANS ∩ CONN = Φ,W-REF ∩ W-UNI = Φ等等。
本文介紹的某些「關係性質」與「單調性」存在一定關係。事實上,根據「定理9」、「定理11」以及相關限定 詞的「單調性」,我們容易推導出某些結果,例如由於"some"以及"(at least n)"是「左、右 遞增」的,我們可以從「定理9(v)」得出以下結論:在LOG ∩ FIN − TRIV下,W-REF ∩ SYM ⊆ ↑MON↑。可是,這樣得來的結果似乎沒有多大意義。為此,我們放寬對限定詞的限制,看看 在這種情況下「關係性質」與「單調性」存在甚麼關係。事實上,我們有以下定理:
| 定理12: | 在CONSr下, |
| (i) REF ∩ TRANS ⊆ ↓MON↑ | |
| (ii) I-REF ∩ AL-CONN ⊆ ↑MON↓ |
以下證明(i),設Q ∈ REF ∩ TRANS,並設Q(A)(B)和A' ⊆ A。根據「自反性」,必有Q(A')(A')
。由於A' ⊆ A,這等價於Q(A')(A' ∩ A)。由此根據「右守恆性」,有Q(A')(A)。根據「傳遞性」,
可以從Q(A')(A)和Q(A)(B)推得Q(A')(B)。至些證得Q ∈ ↓MON。
其次設Q(A)(B)和B ⊆ B'。根據「自反性」,必有Q(B)(B)。由於B ⊆ B',這等價於Q(B)(B ∩
B')。由此根據「右守恆性」,有Q(B)(B')。根據「傳遞性」,可以從Q(A)(B)和Q(B)(B')推得Q(A)(B')。至些
證得Q ∈ MON↑。綜合以上結果,(i)乃得證。
至於(ii),根據「定理1(i)和(vi)」,Q ∈ I-REF ∩ AL-CONN當且僅當~Q ∈ REF ∩
TRANS。根據(i),我們有~Q ∈ ↓MON↑,由此得Q ∈ ↑MON↓,(ii)乃得證。
「對稱性」與「單調性」有一種特殊的聯繫,詳見以下定理:
| 定理13: | 設Q ∈ SYM, |
| (i) Q ∈ ↑MON ⇔ Q ∈ MON↑ | |
| (ii) Q ∈ ↓MON ⇔ Q ∈ MON↓ |
以下只證明(i),(ii)的證明大同小異。設Q ∈ ↑MON,並設Q(A)(B)和B ⊆ B'。根據「對稱性」
,我們有Q(B)(A)。由此根據「左遞增性」,有Q(B')(A)。由此再根據「對稱性」,有Q(A)(B')。至此證明了Q
∈ ↑MON ⇒ Q ∈ MON↑。類似地,我們亦可證明Q ∈ MON↑ ⇒ Q
∈ ↑MON。綜合以上結果,(i)乃得證。
現在如果假設Q ∈ CONSr ∩ SYM,我們將可得到以下結果:
| 定理14: | 在CONSr ∩ SYM下, |
| (i) Q-REF = ↑MON↑ | |
| (ii) Q-UNI = ↓MON↓ |
以下證明(i),首先設Q ∈ Q-REF,並設Q(A)(B)和B ⊆ B'。由於如前所述,在CONSr下,
SYM等價於INT,而A ∩ B = (A ∩ B') ∩ (A ∩ B),我們可以從Q(A)(B)推出Q(A ∩
B')(A ∩ B) (註5)。由此根據Q-REF的定義,有Q(A ∩ B')(A ∩ B')。由此再根據「定理2(v)」,
有Q(A)(B')。至此證得Q ∈ MON↑。根據「定理13(i)」,亦有Q ∈ ↑MON。由此證得Q-REF
⊆ ↑MON↑。
其次設Q ∈ ↑MON↑,並設Q(A)(B)。根據「右守恆性」,有Q(A)(A ∩ B)。由於A ∩ B
⊆ A,由此根據「右遞增性」,有Q(A)(A)。至此證得Q ∈ Q-REF,即↑MON↑ ⊆ Q-REF
。綜合以上結果,(i)乃得證。
(ii)可以證明如下:
| Q ∈ Q-UNI | ⇔ ~Q ∈ Q-REF | (根據「定理1(ii)」) |
| ⇔ ~Q ∈ ↑MON↑ | (根據(i)) | |
| ⇔ Q ∈ ↓MON↓ |


