筆者在《廣義量詞系列:單調性推理原理》和
《廣義量詞系列:單調性推理的擴展》中詳細介紹了量詞的「單調性推理」
。「單調性」在當代形式語言學中是備受關注的課題,可用來解釋多種語言現象,例如筆者在
《日常語言中的梯級推理》一文中便指出,日常語言中常見的「梯級推理」
在本質上便是一種「單調性推理」。
除了前述各篇文章所介紹的「單調性推理」外,「單調性」本身還有很豐富的內容。本文主旨就是介紹當代學
者總結出與「單調性」有關的理論,本文還會介紹「單調性」在當代語言學上的一個重要應用-對自然語言中
各種「極性敏感詞」的語義學解釋。
為簡化討論,本文將集中介紹與「<1,1>型量詞」(即「限定詞」)有關的「單調性」課題。「單調性」是量詞關
於其各個論元的性質,由於限定詞有左、右兩個論元,所以每個限定詞各有左、右兩種「單調性」,即每個限
定詞關於其左/右論元可以是遞增、遞減或非單調的,例如"(more than 10%)"便是「左非單調、右遞
增」的,我們把此一結果標記為
有關「左/右遞增」、「左/右遞減」和「左/右非單調」的定義以及限定詞「單調性」的標記法,請參閱 《廣義量詞系列:單調性推理原理》,茲不贅。
筆者在《廣義量詞系列:單調性推理原理》一文中指出,並非所有限定詞 關於其左、右兩個論元都是遞增/遞減的。Glockner在Fuzzy Quantifiers: A Computational Theory 一書中提出「局部單調性」(Local Monotonicity)的概念,擴大了「遞增/遞減性」的適用性(註1) 。「局部單調性」的要旨是找出左、右論元的變異範圍,使得左、右論元在這個範圍內滿足「遞增/遞減性」 。具體地說,設Q為論域U上的限定詞,X1、Y1、X2、Y2為集 合使得X1 ⊆ X2並且Y1 ⊆ Y2。現設A、A'、B、B' 為集合,那麼Q是在「局部範圍」((X1, Y1), (X2, Y2))內 「局部遞增」(Locally Increasing)的當且僅當
Q是在「局部範圍」((X1, Y1), (X2, Y2))內「局部遞減」 (Locally Decreasing)的當且僅當
在以上定義中,X1、Y1、X2、Y2分別是「局部範圍」的「左
論元下限」、「右論元下限」、「左論元上限」、「右論元上限」。請注意在確定「局部範圍」時,左、右論
元的上、下限往往互相依存,所以在以上定義中,我們難以區分限定詞Q是關於哪一論元「局部遞增/遞減」,
而只能從整體上說Q是「局部遞增/遞減」的。
舉例說,如前所述,"(more than 10%)"是「左非單調、右遞增」的。可是根據Glockner,這個限定詞
在((X, Y), (X ∪ Y, Y))內是「局部遞增」,而在((X, Y), (X ∪ ~Y, Y))內則是「局部遞減」的。以
下首先證明上述「局部遞增範圍」。為方便證明,以下把X和Y寫成不相交集合的并,即
若X ⊆ A ⊆ A' ⊆ X ∪ Y並且Y ⊆ B ⊆ B' ⊆ Y,那麼A、A'、B和B'也可寫 成不相交集合的并:
其中C ⊆ C' ⊆ (Y − X)。根據"(more than 10%)"的真值條件,
容易看到,以上兩個分數的分子之差剛好等於它們的分母之差,即|C' − C|,根據簡單的算術知識,可
知(4)中的分數必定不小於(3)中的分數(註2)。由此可推得,若(3)成立,則(4)必成立,即Q(A)(B) ⇒
Q(A')(B')。
其次證明上述「局部遞減範圍」。同樣,以下把X和~Y寫成不相交集合的并,即
若X ⊆ A' ⊆ A ⊆ X ∪ ~Y並且Y ⊆ B' ⊆ B ⊆ Y,那麼A、A'、B和B'也可寫 成不相交集合的并:
其中D' ⊆ D ⊆ (U − X − Y)。根據"(more than 10%)"的真值條件,
以上兩個分數的分子相同,而(5)中的分母不小於(6)中的分母,因此(6)中的分數必定不小於(5)中的分數。由 此可推得,若(5)成立,則(6)必成立,即Q(A)(B) ⇒ Q(A')(B')。有了「局部單調性」的概念,我們便可 以為每個「非單調限定詞」找出其「局部遞增範圍」及「局部遞減範圍」,這方面的工作還有待展開。
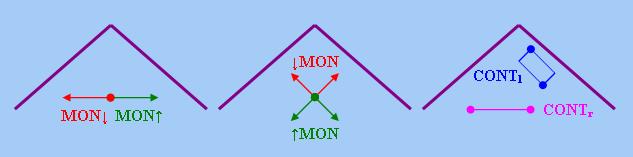
「連續性」(Continuity)是對「單調性」概念的另一種擴展,其定義如下:設Q為限定詞,A、A'、 A''、B、B'、B''為集合,則Q是「左連續」(Left Continuous)的當且僅當
Q是「右連續」(Right Continuous)的當且僅當
以下把由「左連續限定詞」和「右連續限定詞」組成的集合分別記作CONTl和CONTr。 根據上述定義,所有「左(右)遞增/遞減」限定詞都是「左(右)連續」的。此外,某些限定詞雖然在某個論元 上是「非單調」的,但在該論元上卻可以是「連續」的。舉例說,"(exactly n)"雖然是「左、右非單 調」的,但卻是「左、右連續」的,以下是一些推理實例:
「連續性」與「單調性」的關係還體現在以下定理中:
| 定理1: | 設Q為限定詞,則Q ∈ CONTl (CONTr)當且僅當Q = Q1 ∧ Q2,其中Q1 ∈ ↑MON (MON↑) ∧ Q2 ∈ ↓MON (MON↓),而上述等式的意義為對任何A 、B均有,Q(A)(B) ⇔ Q1(A)(B) ∧ Q2(A)(B)。 |
以下證明上述定理,我們僅考慮「左連續性」和「左單調性」的情況。首先,設Q = Q1 ∧
Q2,其中Q1 ∈ ↑MON ∧ Q2 ∈ ↓MON,我們證明
Q ∈ CONTl。為此,設A ⊆ A' ⊆ A'',並且Q(A)(B) ∧ Q(A'')(B)。利用Q =
Q1 ∧ Q2,我們可以把上式改寫為Q1(A)(B) ∧
Q2(A)(B) ∧ Q1(A'')(B) ∧ Q2(A'')(B)。由於Q1
∈ ↑MON ∧ Q2 ∈ ↓MON,我們有Q1(A')(B) ∧
Q2(A')(B),即Q(A')(B),至此證得Q ∈ CONTl。
其次,設Q ∈ CONTl,我們可以定義以下兩個限定詞:
以下先來證明Q1 ∈ ↑MON ∧ Q2 ∈ ↓MON。設A ⊆ A'並
且Q1(A)(B),那麼根據(9),∃C (C ⊆ A ∧ Q(C)(B))。由於A ⊆ A',我們有
∃C (C ⊆ A' ∧ Q(C)(B))。根據(9),有Q1(A')(B),由此證得Q1
∈ ↑MON。利用類似的方法,亦可證得Q2 ∈ ↓MON。
最後證明Q = Q1 ∧ Q2,即對任何A、B,Q(A)(B) ⇔ Q1(A)(B)
∧ Q2(A)(B)。設Q(A)(B),那麼只要把C和D都設定為A,我們便有∃C (C ⊆ A ∧
Q(C)(B)) ∧ ∃D (A ⊆ D ∧ Q(D)(B)),根據(9)和(10),由此證得Q(A)(B) ⇒
Q1(A)(B) ∧ Q2(A)(B)。其次設Q1(A)(B) ∧
Q2(A)(B),那麼根據(9)和(10),∃C (C ⊆ A ∧ Q(C)(B)) ∧ ∃D (A
⊆ D ∧ Q(D)(B)),此即∃C, D (C ⊆ A ⊆ D ∧ Q(C)(B) ∧ Q(D)(B))。由於Q
∈ CONTl,得Q(A)(B),由此證得Q1(A)(B) ∧ Q2(A)(B) ⇒
Q(A)(B)。
「定理1」告訴我們,即使某限定詞Q是「非單調」的,只要它是「連續」的,我們總能把它寫成一個「遞增」
限定詞和一個「遞減」限定詞的合取,(9)和(10)提供這兩個限定詞的公式,由此可見單調限定詞在自然語言中
的重要性。舉例說,"(exactly n)"是「左、右非單調」的,現在我們把它寫成Q1 ∧
Q2。根據(9)和(10),我們有
容易看到,以上兩個限定詞實際分別等同於"(at least n)"和"(at most n)",而這兩個限定詞 正分別是「左、右遞增」和「左、右遞減」的。由此我們有
上述結果符合我們的直觀。當然有一些限定詞具有「左非連續性」(Left Discontinuity)(記作 ~CONTl)或「右非連續性」(Right Discontinuity)(記作~CONTr),例如 "(an even number of)"、"(more than n or fewer than m)"等便是「左、右非連續」的。此 外,"most"也是「左非連續」的,設A = {1},A' = {1, 2},A'' = {1, 2, 3},B = {1, 3},那麼容 易驗證「most(A)(B)」和「most(A'')(B)」成立,但「most(A')(B)」卻不成立。
筆者在《廣義量詞系列:量詞的普遍性質與操作》中介紹了「邏輯限定詞」 的「數字函數」形式,這種函數具有Q[x, y]的形式,並且與「邏輯限定詞」的「集合函數」形式Q(A)(B)存在 以下關係:
上式的理據是「邏輯限定詞」的真值條件只依賴於|A − B|和|A ∩ B|這兩個數值。由於存在上述對 應關係,我們可以把「邏輯限定詞」的「單調性」定義寫成「數字函數」的形式。我們首先考慮較簡單的「右 單調性」的情況。設Q為「邏輯限定詞」,x、y為非負整數,那麼Q是「右遞增」的當且僅當
Q是「右遞減」的當且僅當
以上兩式的理據是,「右單調性」的要旨為在A保持不變的條件下擴大或縮小B。由於|A| = |A − B| +
|A ∩ B|,如要讓A保持不變,我們必須使「數字函數」的兩個論元之和保持不變。如要在此條件下擴大(縮
小) B,便必須使Q的第二論元增加(減小)為y',並同時保持x + y = x' + y'。
從以上兩式,容易得到「右連續性」的定義,即Q是「右連續」的當且僅當
「左單調性」的情況則大為不同。儘管「左單調性」的要旨為在B保持不變的條件下擴大或縮小A,但由於Q的「 數字函數」形式並不包含|B − A|的信息,我們無法像(13)和(14)那樣用x和y來表達「B保持不變」這個 條件。不過,我們仍然有以下定義:Q是「左遞增」的當且僅當
Q是「左遞減」的當且僅當
以下證明Q ∈ ↑MON的「數字函數」定義(即(16))與通常的「集合函數」定義等價(Q ∈
↓MON的證明大同小異)。首先設(16)成立,並設Q(A)(B)和A ⊆ A',那麼根據(12),有Q[|A −
B|, |A ∩ B|]。從A ⊆ A'可以推出|A − B| ≤ |A' − B| ∧ |A ∩ B| ≤
|A' ∩ B|。由此根據(16),有Q[|A' − B|, |A' ∩ B|]。根據(12),此即Q(A')(B),由此證得在
「集合函數」定義下,Q ∈ ↑MON。
其次設在「集合函數」定義下,Q ∈ ↑MON,並設Q[x, y]和x ≤ x' ∧ y ≤ y',那麼根據
(11),存在A、B使得|A − B| = x,|A ∩ B| = y,並且Q(A)(B)。接著我們選取A'使得A ⊆ A'
並且|A' − B| = x',|A' ∩ B| = y' (請注意根據「擴展性」,我們可以任意擴大論域,從而保證
必能選取所需的A')。由於Q ∈ ↑MON,必有Q(A')(B)。根據(12),此即Q[x', y'],由此證得(16)成
立。
從(16)和(17),容易得到「左連續性」的定義,即Q是「左連續」的當且僅當
筆者在上述網頁亦介紹了「數字三角形」的概念,指出可以用這種圖形來表示各種「有限論域邏輯限定詞」的 真值條件以及量詞的各種普遍性質,上述結論當然也適用於「單調性」。「數字三角形」就是由「+」號和 「−」號組成的三角形,三角形上的位置代表數字有序對[x, y],以下是這些有序對在三角形上的分佈情 況:
| [x, y] | |
|---|---|
| x + y = 0 | |
| x + y = 1 | |
| x + y = 2 | |
| x + y = 3 | |
| : |
「數字三角形」上對應著有序對[x, y]的位置如有「+」號或「−」號,代表Q[x, y]為真或假。利用「數
字三角形」,我們便可以形象地表達「單調性」和「連續性」。為方便表達在「數字三角形」上移動的方向,
以下沿用Peters and Westerstahl在Quantifiers in language and logic一書中的做法,把「數字三
角形」看作平面地圖,並把豎直向上的方向作為北方。首先,在「數字三角形」中,每一橫行代表某一固定的x
+ y值,而在同一橫行上向東(西)移動代表在維持x + y不變的情況下減少(增加) x值並同時增加(減少) y值。
由此根據(13)-(15),「右遞增(遞減)性」在「數字三角形」上表現為,假如某一位置有「+」號,那麼與該位
置處於同一橫行並在該位置東邊(西邊)的所有其他位置都應有「+」號;而「右連續性」則表現為,假如某一橫
行上的兩個位置有「+」號,那麼夾於該兩個位置之間的所有其他位置都應有「+」號。
以下給出滿足「右遞增性」、「右遞減性」和「右連續性」的「數字三角形」的例子:
除了橫行外,「數字三角形」還包含著兩種平行的斜行:東北-西南走向的斜行(例如由[0, 1]、[1, 1]、[2,
1]組成的斜行)和西北-東南走向的斜行(例如由[1, 0]、[1, 1]、[1, 2]組成的斜行)。容易看到,從「數字三
角形」上某一位置出發,若沿著所在斜行朝西南(東北)方向移動,數字有序對的第二數值保持不變,而第一數
值則遞增(遞減);若沿著所在斜行朝東南(西北)方向移動,則數字有序對的第一數值保持不變,而第二數值則
遞增(遞減)。
此外,如在「數字三角形」上任取兩個位置[x, y]和[x'', y'']使得x ≤ x'' ∧ y ≤ y'',那麼所有
滿足x ≤ x' ≤ x'' ∧ y ≤ y' ≤ y''的[x', y']組成一個平行四邊形,這個平行四邊形以上述
兩個位置為端點,並以該兩個位置所在斜行為邊。例如如果選取[0, 1]和[1, 2]這兩個位置,那麼由[0, 1]、
[1, 1]、[0, 2]、[1, 2]組成的平行四邊形便包含著所有[x', y']使得0 ≤ x' ≤ 1 ∧ 1 ≤ y'
≤ 2。
由此根據(16)-(18),「左遞增(遞減)性」在「數字三角形」上表現為,假如某一位置有「+」號,那麼與該位
置處於同一斜行並在該位置西南方(東北方)或東南方(西北方)的所有其他位置都應有「+」號;而「左連續性」
則表現為,假如某兩個位置[x, y]和[x'', y'']有「+」號,而且該兩個位置滿足x ≤ x'' ∧ y ≤
y'',那麼上述平行四邊形內的所有其他位置都應有「+」號。
以下給出滿足「左遞增性」、「左遞減性」和「左連續性」的「數字三角形」的例子:
|
|
||||
現把上述各種性質在「數字三角形」上的反映總結為下圖:

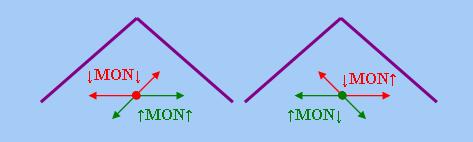
上節的圖顯示,代表「左遞增/遞減性」的圖形各由兩個箭頭組成,這告訴我們「左遞增/遞減性」可以分解
為更基本的概念。正是基於此一觀察,Peters and Westerstahl提出六種「基本單調性」,分別代表
上圖中六個不同方向的箭頭。在這六種「基本單調性」中,兩種屬於「右單調性」,此即「右遞增性」和「右
遞減性」。如前所述,這兩種「右單調性」較為簡單,可以分別用東向和西向的箭頭代表,所以它們本身便屬
於「基本單調性」。
其餘四種「基本單調性」則屬於「左單調性」,可分別用東南、西南、西北和東北方向的箭頭代表,前兩種為
「左遞增性」,後兩種為「左遞減性」。以下列出這四種「基本單調性」的「數字函數」和「集合函數」定義
。設Q為限定詞,x、x'、y、y'為非負整數,A、A'、B為集合,則Q是「東南方向遞增」(記作
↑SEMON)的當且僅當
或者
Q是「西南方向遞增」(記作↑SWMON)的當且僅當
或者
Q是「西北方向遞減」(記作↓NWMON)的當 且僅當
或者
Q是「東北方向遞減」(記作↓NEMON)的當且僅當
或者
下圖顯示上述四種「基本單調性」:

請注意上述四種「基本單調性」之間存在微妙的關係。舉例說,設Q ∈ ↑SEMON,即Q滿 足(20)。我們可以把(20)改寫為
上述條件等價於
根據(22),我們有Q~r ∈ ↑SWMON,由此證得Q ∈ ↑SEMON ⇒ Q~r ∈ ↑SWMON。同理亦易證Q ∈ ↑SWMON ⇒ Q~r ∈ ↑SWMON,由此可知 ↑SEMON與↑SWMON互為「右補性質」。根據相似的推理,亦可證明 ↓NWMON則與↓NEMON互為「右補性質」。
我們可以把上述六種「基本單調性」兩兩加以組合,從而得到各種複合性質。如前所述,傳統的兩種「左單調 性」便可以看成「基本單調性」的複合,即
請注意上式顯示,傳統的兩種「左單調限定詞」是相關的「基本單調限定詞」的子集。事實上,根據上一小節
的定義,所有「左遞增限定詞」都同時滿足(20)和(22),而所有「左遞減限定詞」都同時滿足(24)和(26)。
限定詞的「左、右單調性」也可看成兩種「基本單調性」的複合。以↑MON↑為例,這個「單調性」似
乎是三種「基本單調性」複合的結果,即↑SEMON ∩ ↑SWMON ∩
MON↑。可是在上式中,↑SEMON是多餘的,這是因為
證明如下:設Q ∈ ↑SWMON ∩ MON↑、x = x' ∧ y ≤ y',並且Q[x, y]
。取x'' = x + (y' − y)和y'' = y,那麼根據(21),有Q[x'', y'']。由於y'' ≤ y'並且x'' + y''
= x' + y',根據(13),我們有Q[x', y']。由此根據(19),證得Q ∈ ↑SEMON。
請注意上述證明其實利用了以下原理,如要向東南方某位置移動,可以先向西南方移動至與該位置同一緯度上
的位置,然後朝正東方移動至該位置。由此我們可以把全部四種「左、右單調性」都看成兩種「基本單調性」
的複合:
現把上述結果總結成下圖:
「基本單調性」的以下四種複合在自然語言中似乎難以找到對應概念:↓NEMON ∩ MON↑、↑SWMON ∩ MON↓、↑SEMON ∩ MON↑、 ↓NWMON ∩ MON↓。不過,如果我們定義以下限定詞(在以下定義中,n為自然數,q為 小於1的分數):
那麼我們有
現證明(33)和(35)如下,(34)和(36)的證明大同小異。先證(33),容易看到Q1 ∈ MON↑
,所以以下只證Q1 ∈ ↓NEMON。設Q1(A)(B)以及A' ⊆ A
∧ A ∩ B = A' ∩ B,那麼根據Q1的真值條件,我們有|A| ≤ n ∧ |A ∩ B|
/ |A| ≥ q。根據設定條件,我們亦有|A'| ≤ |A| ∧ |A ∩ B| = |A' ∩ B|,由此得|A'|
≤ |A| ≤ n ∧ |A' ∩ B| / |A'| ≥ |A ∩ B| / |A| ≥ q,因此Q1(A')(B)
。根據(26),證得Q1 ∈ ↓NEMON。
其次證(35),容易看到Q3 ∈ MON↑,所以以下只證Q3 ∈
↑SEMON。設Q3(A)(B)以及A ⊆ A' ∧ A − B = A' − B,那
麼根據Q3的真值條件,我們有|A| ≥ n ∧ |A − B| / |A| ≤ q。根據設定條件,
我們亦有|A| ≤ |A'| ∧ |A − B| = |A' − B|,由此得|A'| ≥ |A| ≥ n ∧ |A'
− B| / |A'| ≤ |A − B| / |A| ≤ q,因此Q3(A')(B)。根據(20),證得
Q3 ∈ ↑SEMON。
可是,上述Q1-Q4是否對應著自然語言中的任何限定詞?根據Peters and
Westerstahl,Q1在自然語言中可以用"(at least q of n or fewer)"來表達(註3)。類似
地,我們也可以用"(at most q of n or more)"來表達Q2。至於Q3和
Q4,根據以下關係:|A − B| / |A| ≤ q ⇔ |A ∩ B| / |A| ≥ 1 − q
,我們可以把它們分別表達為"(at least 1 − q of n or more)"和"(at most 1 − q
of n or fewer)"。
最後,請注意(33)-(36)只提供了上述四種複合的一些特例,並未概括出這四種複合的本質屬性。現把(33)-
(36)總結成下圖:

把六種「基本單調性」兩兩組合,共有15種可能性,在上一小節,我們已討論了其中10種可能組合((27)- (36));在本小節,我們將研究其餘5種組合,這5種組合各對應著一種特殊的限定詞性質。首先考慮MON↑ ∩ MON↓,這類限定詞在「數字三角形」上表現為,如果某位置有「+」號,那麼處於該位置所在橫行 並在該位置東邊和西邊的所有其他位置都有「+」號。換句話說,對於每個橫行而言,要麼整行都是「+」號, 要麼整行都是「−」號。這類限定詞的真值條件只依賴於|A|,在文獻上這種性質稱為「反歐幾里德 性」(Antieuclidity)(註4),即Q是「反歐幾里德」的當且僅當
以下把由「反歐幾里德限定詞」組成的集合記作AN-EUCLID。根據上述討論,我們有
容易看到,兩個「平凡限定詞」1(A)(B) ⇔ A = A和0(A)(B) ⇔ A ≠ A都是「反歐幾里德」的,由 此可見,「反歐幾里德性」是「平凡性」概念的推廣。在自然語言中,"(some or none of n)"和 "(some or none of n or more)"似乎就是「反歐幾里德限定詞」的例子,因為我們可以把這兩個限定 詞的真值條件定為
筆者在《廣義量詞系列:量詞的代數性質》中介紹了「相交性」 (記作INT)和「右補相交性」(記作RC-INT),這兩種性質表面上看跟「單調性」沒有甚麼關連,但其 實都可看成兩種「基本單調性」的複合,即
以上兩個等式顯示,若Q ∈ INT,則Q的「數字三角形」每條東北-西南走向的斜行要麼全為「+」號,要麼 全為「−」號。同理,若Q ∈ RC-INT,則Q的「數字三角形」每條西北-東南走向的斜行要麼全為「+ 」號,要麼全為「−」號。由此我們有以下結果:Q是「相交」的當且僅當
Q是「右補相交」的當且僅當
為證明(38)和(39),我們要使用以下兩個定理:
| 定理2: | 「相交性」的以下兩個定義是等價的: |
| (i) 若A ∩ B = C ∩ D,則Q(A)(B) ⇔ Q(C)(D)。 | |
| (ii) 對任何A、B,Q(A)(B) ⇔ Q(A ∩ B)(A ∩ B)。 |
| 定理3: | 「右補相交性」的以下兩個定義是等價的: |
| (i) 若A − B = C − D,則Q(A)(B) ⇔ Q(C)(D)。 | |
| (ii) 對任何A、B,Q(A)(B) ⇔ Q(A − B)(~(A − B))。 |
現證明「定理2」。首先設(i)成立,並取C = D = A ∩ B,那麼A ∩ B = C ∩ D,由此必有Q(A)(B)
⇔ Q(C)(D) = Q(A ∩ B)(A ∩ B),即(ii)成立。其次設(ii)成立以及A ∩ B = C ∩ D,那
麼必有Q(A)(B) ⇔ Q(A ∩ B)(A ∩ B) = Q(C ∩ D)(C ∩ D) ⇔ Q(C)(D),即(i)成立
。
接著證明「定理3」。首先設(i)成立,並取C = A − B,D = ~(A − B),那麼A − B = C
− D,由此必有Q(A)(B) ⇔ Q(C)(D) = Q(A − B)(~(A − B)),即(ii)成立。其次設
(ii)成立以及A − B = C − D,那麼必有Q(A)(B) ⇔ Q(A − B)(~(A − B)) =
Q(C − D)(~(C − D)) ⇔ Q(C)(D),即(i)成立。
借助「定理2」,我們可以證明(38)。首先設Q ∈ INT,並設Q(A)(B)和A ⊆ A' ∧ A ∩ B =
A' ∩ B,那麼根據「定理2(i)」,有Q(A')(B)。由此根據(22),證得Q ∈ ↑SWMON。
現在再設Q(A)(B)和A' ⊆ A ∧ A ∩ B = A' ∩ B,那麼根據「定理2(i)」,有Q(A')(B)。由此
根據(26),證得Q ∈ ↓NEMON。綜合以上結果,我們有INT ⊆
↑SWMON ∩ ↓NEMON。
其次設Q ∈ ↑SWMON ∩ ↓NEMON,我們要證明「定理2(ii)」成立。
為此,設Q(A)(B)。由於A ∩ B ⊆ A並且A ∩ B = (A ∩ B) ∩ B,根據(26),有Q(A ∩
B)(B)。根據「右守恆性」(註5),有Q(A ∩ B)(A ∩ B)。由此證得Q(A)(B) ⇒ Q(A ∩ B)(A
∩ B)。現在再設Q(A ∩ B)(A ∩ B)。由於A ∩ B ⊆ A並且(A ∩ B) ∩ (A ∩
B) = A ∩ (A ∩ B),根據(22),有Q(A)(A ∩ B)。再根據「右守恆性」,有Q(A)(B)。由此證得
Q(A ∩ B)(A ∩ B) ⇒ Q(A)(B)。至此我們證明了「定理2(ii)」成立,由此得
↑SWMON ∩ ↓NEMON ⊆ INT。綜合以上結果,(38)得證。
借助「定理3」,我們可以證明(39)。首先設Q ∈ RC-INT,並設Q(A)(B)和A ⊆ A' ∧ A −
B = A' − B,那麼根據「定理3(i)」,有Q(A')(B)。由此根據(20),證得Q ∈
↑SEMON。現在再設Q(A)(B)和A' ⊆ A ∧ A − B = A' − B,那麼根據「
定理3(i)」,有Q(A')(B)。由此根據(24),證得Q ∈ ↓NWMON。綜合以上結果,我們有
INT ⊆ ↑SEMON ∩ ↓NWMON。
其次設Q ∈ ↑SEMON ∩ ↓NWMON,我們要證明「定理3(ii)」成立。
為此,設Q(A)(B)。由於A − B ⊆ A並且A − B = (A − B) − B,根據(24),有
Q(A − B)(B)。根據「右守恆性」,有Q(A − B)(~(A − B))。由此證得Q(A)(B) ⇒
Q(A − B)(~(A − B))。現在再設Q(A − B)(~(A − B))。由於A − B ⊆ A
並且(A − B) − ~(A − B) = A − ~(A − B),根據(20),有Q(A)(~(A −
B))。再根據「右守恆性」,有Q(A)(B)。由此證得Q(A − B)(~(A − B)) ⇒ Q(A)(B)。至此我
們證明了「定理3(ii)」成立,由此得↑SEMON ∩ ↓NWMON ⊆
RC-INT。綜合以上結果,(39)得證。
由「基本單調性」複合而成的最後兩種性質是「光滑性」(Smoothness)(記作SMO)和「右補光滑
性」(Right-Complemented Smoothness)(記作RC-SMO),其定義如下:
容易看到「右補光滑性」的確是「光滑性」的「右補」性質,這是因為構成「右補光滑性」的兩種「基本單調
性」正好分別是構成「光滑性」的某種「基本單調性」的「右補」性質。
自然語言中有哪些量詞屬於SMO或RC-SMO?筆者在5.2小節證明了Q1和Q3分別屬於
↓NEMON和↑SEMON。如果略去這兩個量詞真值條件中有關|A|的部分,那麼這
兩個量詞分別相等於"(at least q)"和"(at least 1 − q)"。由於q和1 − q是任
意分數,所以我們得到(at least q) ∈ SMO。請注意"(at least q)"是「左非單調」的,
但卻具有兩種「左基本單調性」,由此可見「基本單調性」是對傳統「單調性」概念的另一種推廣。
根據上述結果以及(20)和(26),我們有以下兩個推理實例:
請注意在上面第一個推理中,我們是以一個否定概念來定義B (即「不參加女子體操隊的個體」),從而
使A − B和A' − B變成肯定概念,(即分別等於「參加女子體操隊的女生」和「參加女子體操隊的
學生」。這樣做的原因是在日常語言中,難以找到否定概念A − B和A' − B使A − B = A'
− B成立。
同理,我們亦可推得(at most q) ∈ RC-SMO (註6)。根據上述結果以及(22)和(24),我們有以下
兩個推理實例:
「光滑性」和「右補光滑性」與「右單調性」存在特殊的關係,我們可以從這兩種性質分別推出「右遞增性」 和「右遞減性」,即
直觀地說,上述結果反映了如下事實:如要朝東(西)方移動,可以先向東北(西北)方移動一段適當距離,然後 向東南(西南)方移動同一個距離。現把本小節介紹的五種性質總結成下圖:

「單調性」與三種「布爾運算」(即集合論上的「并」、「交」、「補」和邏輯學上的「析取」、「合取」、「 否定」)存在微妙的關係,本小節首先討論與「并/析取」和「交/合取」有關的某些限定詞性質,這些性質統 稱為「加乘性質」(註7)。為簡化討論,以下筆者集中討論「右論元」的情況,惟請注意,以下介紹 的內容都可推廣至「左論元」。首先看以下定理:
| 定理4: | 以下命題等價: |
| (i) Q ∈ MON↑ | |
| (ii) 對任何A、B、B',Q(A)(B ∩ B') ⇒ Q(A)(B) ∧ Q(A)(B')。 | |
| (iii) 對任何A、B、B',Q(A)(B) ∨ Q(A)(B') ⇒ Q(A)(B ∪ B')。 |
| 定理5: | 以下命題等價: |
| (i) Q ∈ MON↓ | |
| (ii) 對任何A、B、B',Q(A)(B ∪ B') ⇒ Q(A)(B) ∧ Q(A)(B')。 | |
| (iii) 對任何A、B、B',Q(A)(B) ∨ Q(A)(B') ⇒ Q(A)(B ∩ B')。 |
以下僅證明「定理5」(「定理4」的證明大同小異)。首先證(i) ⇒ (ii),設(i)成立並且Q(A)(B ∪
B')。由於B ∪ B'是B和B'的母集,根據(i),必有Q(A)(B) ∧ Q(A)(B')。其次證(ii) ⇒ (iii),
設(ii)成立並且Q(A)(B) ∨ Q(A)(B')。由於B = B ∪ (B ∩ B'),根據(ii),我們可以從Q(A)(B)推
得Q(A)(B) ∧ Q(A)(B ∩ B'),由此又可推得Q(A)(B ∩ B')。同樣,由於B' = B' ∪ (B ∩
B'),我們也可以從Q(A)(B')推得Q(A)(B ∩ B')。綜合以上兩個推理,得到(ii) ⇒ (iii)成立。最後
用反證法來證明(iii) ⇒ (i),設(iii)成立並且Q(A)(B)和B' ⊆ B,但~Q(A)(B')。當B' ⊆ B時
,B' = B ∩ B'。而(iii)的逆否定命題為~Q(A)(B ∩ B') ⇒ ~(Q(A)(B) ∨ Q(A)(B')),由此可
推得~Q(A)(B) ∧ ~Q(A)(B'),但這與Q(A)(B)矛盾,至此定理得證。
為方便以下討論,首先定義下表所示的各種「基本加乘性質」(在以下定義中,Q為限定詞,A、B、B'
為集合):
| 名稱 | 代號 | 定義 |
|---|---|---|
|
|
||
從上表的定義以及「定理4」和「定理5」,我們有
由此可見,在上述八種「基本加乘性質」中,其中四種其實等價於「右遞增/遞減性」。現在我們把這四種「 基本加乘性質」跟其餘四種結合,從而得到四種「加乘性質」。下表列出這四種「加乘性質」的定義:
| 名稱 | 代號 | 定義 |
|---|---|---|
|
|
||
|
|
||
從上表的定義可見,各種「加乘性質」其實就是相應的「次加乘性質」和「超加乘性質」的結合,即
比較(44)-(47)與(42)、(43),我們也可看到「右可加/可乘限定詞」都是「右遞增」,而「右反加/反乘限
定詞」都是「右遞減」的,因此各種「加乘性質」其實都是「單調性」的次類。
根據限定詞的真值條件,我們可以確定自然語言中具有上述四種「加乘性質」的限定詞的例子,例如
其中"some"的「右可加性」可證明如下:首先設some(A)(B ∪ B'),由此我們有
| A ∩ (B ∪ B') ≠ Φ | |
| ⇔ | (A ∩ B) ∪ (A ∩ B') ≠ Φ |
| ⇔ | (A ∩ B) ≠ Φ ∨ (A ∩ B') ≠ Φ |
上面最後一行告訴我們some(A)(B) ∨ some(A)(B'),至此證明了"some"是「右可加」
的。
以下是上述結果的推理實例:
請注意並非所有「右遞增(遞減)限定詞」都具有「右可加/可乘(反加/反乘)性」,舉例說,「右遞減限定詞」 "(at most n)"便既非「右反加」亦非「右反乘」,這可以從以下兩個無效推理得到證實:
上面第一個無效推理的反例是,論域中共有四名學生A、B、C、D,其中只有A和B唱歌,並且只有C和D跳舞。在 此情況下,左邊的語句是假的,但右邊的語句卻是真的。第二個無效推理的反例則是,論域中共有四名學生A、 B、C、D,其中只有A、B、C唱歌,並且只有B、C、D跳舞。在此情況下,左邊的語句是真的,但右邊的語句卻是 假的。上述例子顯示,A-ADDr和A-MULTr是MON↓的真子集。同理,我們也不難找 到例子顯示ADDr和MULTr是MON↑的真子集。
在本小節,筆者首先介紹下表所示三種與「補/否定」有關的性質(在以下定義中,Q為限定詞,A、B為集合) (註8):
| 名稱 | 代號 | 定義 |
|---|---|---|
|
|
||
|
|
||
|
|
從上述定義可見,「右自對偶性」其實是「右協調性」與「右完備性」的結合,即
「右自對偶性」跟上一小節介紹的四種「加乘性質」存在以下關係:
| 定理6: | (i) ADDr ∩ SDr ⊆ MULTr |
| (ii) MULTr ∩ SDr ⊆ ADDr |
| 定理7: | (i) A-ADDr ∩ SDr ⊆ A-MULTr |
| (ii) A-MULTr ∩ SDr ⊆ A-ADDr |
| Q(A)(B ∪ B') | ||
| ⇔ | Q(A)(~(~B ∩ ~B')) | (根據「德.摩根律」) |
| ⇔ | ~Q(A)(~B ∩ ~B') | (根據SDr的定義) |
| ⇔ | ~(Q(A)(~B) ∨ Q(A)(~B')) | (根據A-MULTr的定義) |
| ⇔ | ~Q(A)(~B) ∧ ~Q(A)(~B') | (根據「德.摩根律」) |
| ⇔ | Q(A)(B) ∧ Q(A)(B') | (根據SDr的定義) |
由此證得Q ∈ A-ADDr。
把「右自對偶性」與各種「加乘性質」結合,便可定義下表所示的性質:
| 名稱 | 代號 | 定義 |
|---|---|---|
|
|
||
|
|
根據上表的定義和「定理6」,一個「右同態」限定詞Q具有「右可加性」、「右可乘性」和「右自對偶性」這
三種性質,即Q可把其第二論元上的「并」、「交」、「補」運算轉化為整個量化句的「析取」、「合取」、「
否定」運算,這就是「右同態」一名的由來(註9)。類似地,根據上表和「定理7」,一個「右反態」限定詞Q具
有「右反加性」、「右反乘性」和「右自對偶性」這三種性質,即Q可把其第二論元上的「并」、「交」、「補
」運算轉化為整個量化句的「合取」、「析取」、「否定」運算,這就是「右反態」一名的由來。
自然語言中是否存在「右同態」或「右反態」限定詞?答案是表示個體的限定詞"the (one)" (其後須
為單數名詞)是「右同態」的,這可以從以下推理實例中得到驗證:
如果我們把考慮的範圍擴大至「<−,1>型量詞」,那麼我們將發現單數專有名詞"John"等也是「
同態」量詞(註10)。
至於「(右)反態」量詞,則情況較為複雜。從邏輯上說,上述「(右)同態」量詞的否定都具有「(右)反態性」
。可是,自然語言似乎沒有"(not the (one))"這樣的否定限定詞。至於"(not John)"這樣的否
定專有名詞,其在日常語言中的使用似乎很受限制,儘管Zwarts在Three Types of Polarity一文中曾
舉出以下推理實例以驗證"not + 專有名詞"的「右反乘性」:
筆者在《廣義量詞系列:量詞的普遍性質與操作》中曾指出,我們可以把 二元「命題聯結詞」 "if" 、 "and" 、 "or" 、"without"等處理成「真值限 定詞」,例如"without"的真值條件是
把這些「命題聯結詞」看成限定詞,我們便可以研究它們的各種「加乘性質」。舉例說,我們有
如果我們把考慮的範圍擴大至一元「命題聯結詞」"not",那麼我們將發現這個「命題聯結詞」具有「
反態性」,證明如下:首先設not(p ∨ q),轉換為命題邏輯中的通常形式就是~(p ∨ q)。根據「
德.摩根律」,這等價於~p ∧ ~q,亦即not(p) ∧ not(q),由此證得"not"具有
「反加性」。其次設not(~p),轉換為命題邏輯中的通常形式就是~(~p),但這又可以轉換為
~(not(p)),由此證得"not"具有「自對偶性」。
現把本節介紹的各種性質與「右單調性」和「右連續性」的關係總結成下圖:

在本節,筆者將介紹「單調性」在「極性敏感詞」(Polarity Sensitive Item)上的應用。在語法學 上,「極性」(Polarity)是「肯定」和「否定」的統稱。以往的語法學家認為,自然語言中某些詞項的合法性 取決於句子的「極性」,故把這類詞項統稱為「極性敏感詞」。「極性敏感詞」可分為兩類,「負極性詞」 (Negative Polarity Item)只能出現於「否定語境」中,例如英語的"any"就是如此,試比較以下兩句:
反之,「正極性詞」(Positive Polarity Item)則被「否定」語境排斥,例如英語的"already"就是 如此,試比較以下兩句:
可是,後來有一些語言學家(例如Ladusaw)指出,「極性敏感詞」的合法性並非完全取決於「否定語境」,例如 下句雖然沒有否定詞,但"any"在下句中卻是合法的:
Ladusaw提出「極性敏感詞」的合法性乃取決於比「否定語境」範圍更廣的「遞減語境」。事實上,上述兩個包
含"any"的句子的共同點是兩者的"any"都處於「遞減語境」中,即否定詞"not"和「右遞減限定詞」"at most
three"為"any"提供了所需的「遞減語境」。
後來,有一些語言學家(例如Zwarts、van der Wouden等)進一步發現,「遞減語境」仍然不足以解釋「極性敏
感詞」的語法表現,這是因為每一個「極性敏感詞」在不同的「遞減語境」下可能有不同的語法表現。因此,
他們主張把「遞減語境」區分為三個「否定層級」,分別對應著三類性質。第一個層級稱為「經典否定」
(Classical Negation),對應著「反態性」,造成此一層級的詞項是典型的否定詞"not"。第二個
層級稱為「正規否定」(Regular Negation),對應著「反加性」,造成此一層級的典型詞項是限定詞
"no"。第三個層級稱為「極小否定」(Minimal Negation),對應著「遞減性」,造成此一層
級的典型詞項是限定詞"(at most n)" (註12)。
從上述分級可見,「經典否定」就是傳統的否定概念,其餘兩個層級則是對傳統否定概念的推廣。從「否定性」
(Negativity)的角度來看,「經典否定」的「否定性」最強,「極小否定」的「否定性」最弱,「正規否定」
則介乎兩者之間。
van der Wouden在Negative contexts: collocation, polarity and multiple negation一書中提出把 「極性敏感詞」分為「強」(Strong)、「中」(Medium)、「弱」(Weak)三個類別,這三個類別在上述三種「否 定層級」中各有不同的語法表現。下表是van der Wouden總結出來的結果(下表亦列出各類「極性敏感詞」的例 子以及造成各種「否定層級」的典型限定詞/命題聯結詞):
| 強負極性詞 "a bit" | 中負極性詞 "yet" | 弱負極性詞 "any" | 強正極性詞 "allerminst" | 中正極性詞 "een beetje" | 弱正極性詞 "al" |
|
|---|---|---|---|---|---|---|
| 極小否定 (at most n) |
| |||||
| 正規否定 no |
| |||||
| 經典否定 not |
上表中的「+」和「−」分別代表「合法」和「不合法」。上表顯示,只有「弱負極性詞」才可同時出現
於三種「否定層級」中,並且只有「強正極性詞」才同時被三種「否定層級」排斥,其餘各類「極性敏感詞」
的語法表現則介乎這兩個極端之間。以下提供上述六類「極性敏感詞」在各種「否定層級」中的例句,這些「
否定層級」都處於右論元中。在以下例句中,藍色粗體詞代表造成「否定層級」的詞項,紅色詞
則代表「極性敏感詞」。首先看「負極性詞」,全部例句都來自英語。
「強負極性詞」:
「中負極性詞」:
「弱負極性詞」:
其次看「正極性詞」,由於英語在這方面的表現不太典型,以下採用荷蘭語的例子:
「強正極性詞」:
|
| ||||
| =「最 多四顆星星一閃也不閃。」 |
|
| ||||
| =「沒 有人一點也不高興。」 |
|
| |||||
| =「老師不是一點也不高興。」 |
「中正極性詞」:
|
| ||||
| =「最多 四顆星星閃了閃。」 |
|
| ||||
| =「沒有人 感到有點高興。」 |
| =「老師不是有點高興。」 |
「弱正極性詞」:
|
| door | mensen | bezocht. | ||||
| =「最多七顆彗星已被人探訪過。」 |
| =「沒有人 已感到高興。」 |
| =「老師不是已感到高興。」 |
除了上述六類「極性敏感詞」外,van der Wouden其實還討論了少數兼有「正極性詞」和「負極性詞」特點的 「二極性詞」(Bipolar Item)以及只能出現於「反乘性」語境的詞項。由此可見,表5並未概括自然語言中的所 有「極性敏感詞」,這一課題還有待學者繼續深入研究。
在前面,筆者一直集中討論右論元上的「加乘性質」、「同態/反態性」以及「極性敏感」現象,但上述概念 和結果其實都可推廣至左論元。在本小節筆者無意重新介紹各種概念和結果,只想討論兩個較為特別的限定詞 -"every"和"without"。根據前面的討論,"every"和"without"都具有「右可 乘性」,所以「負極性詞」不能出現於它們的右論元位置。但若從左論元的角度考慮,則情況會大為不同。容 易證明,"every"和"without"都具有「左反加性」,其中"without"的「左反加性」可 證明如下:設without(p ∨ p')(q),由此我們有
| ~(p ∨ p') ∧ q | |
| ⇔ | ~p ∧ ~p' ∧ q |
| ⇔ | (~p ∧ q) ∧ (~p' ∧ q) |
上面最後一行告訴我們without(p)(q) ∧ without(p')(q),至此證明了"without"
是「左反加」的。
由此可知,"every"和"without"都可以在其左論元上造成「正規否定」語境,因此根據表5,其
左論元應容許「中負極性詞」、「弱負極性詞」和「弱正極性詞」並且排斥「強負極性詞」、「強正極性詞」
和「中正極性詞」。以下提供這兩個詞項與某些荷蘭語「正極性詞」共用的例句。首先看"every"的例
句:
| mager | zijn | worden | geslacht. | ||||
|
| |||||||
| =「所有連一點瘦肉也沒有的豬都會被屠宰。」 | |||||||
| vet | zijn | worden | geslacht. | ||||
|
| |||||||
| =「所有有點兒肥的豬都會被屠宰。」 | |||||||
| vet | zijn | worden | geslacht. | ||||
|
| |||||||
| =「所有已變肥的豬都會被屠宰。」 | |||||||
請注意上面各句都使用「關係分句」的形式把包含「正極性詞」的成分嵌入到左論元(即主語)中。其次看 "without"的例句:
|
| allerminst | verheugd | was. (註13) | |||
|
| 是 | |||||
| =「國王到達後該國並非沒有絲毫歡欣。」 | ||||||
| een beetje | schade aan | te richten. | |||
|
| |||||
| =「暴風雨過後並沒有造成一點損壞。」 | |||||
|
| het hele | geheim | te vertellen. | |||||
| =「國王提供了一個線索但並未透露整個秘密。」 | ||||||||
請注意由於"zonder"是一個介詞,它通常都出現於句中而非句首,所以其右論元常常被置於其前。換句話說, 我們要把上面各句的表層形式"q zonder p"理解成"without(p)(q)"。
註1:Glockner採用的概念是「非遞減」(Non-decreasing)和「非遞增」(Non-increasing),跟本文的概念略有 不同,因此以下對Glockner的定義略作修改。

