日常語言中的梯級推理

1. 引言

「推理」在一般人心目中似乎是一種學術味很濃，專屬於某些「智者」的活動，但根據當代語義-語用學家的研 究，「推理」其實是一般人日常語言中的必要元素。沒有「推理」，人們幾乎無法進行交談。在日常語言的各 種推理中，有一種頗為特別的「梯級推理」(Scalar Reasoning)，以往較少人作系統研究，但卻是一 種頗常見的推理，其應用涉及多個語言層面，本文將簡介這種推理。

本文的「梯級」(Scale)是指由一些詞項組成的「序列」(Sequence)，這些詞項的排序方式可以依照 各種各樣的理據，既可以是數學／邏輯／語義方面的理據，也可以是語用／修辭／慣用法方面的理據，因而便 產生不同類型的「梯級推理」。

2. 量詞的單調性推理

「單調性推理」(Monotonic Inference)是當代「廣義量詞理論」(Generalized Quantifier Theory) 研究的一種推理。簡言之，「單調性推理」是有關把某一真「量化句」(註1)中的「論元」換成其母集 (Superset)／子集(Subset)後，所得語句是否仍然為真的推理。舉例說，設以下兩個語句為真：

容易看到對於上面第一句，如果把其左論元(相當於「主語」)「小學生」換成其真母集「學生」，並把右論元 (相當於「謂語」)「跑步」換成其真母集「做運動」，所得語句仍然為真。至於第二句，如果把其左論元「小 學生」換成其真子集「小一學生」，並把右論元「跑步」換成其真母集「做運動」，所得語句仍然為真，即

上述結果不是偶然的，而是「有」和「所有」這兩個量詞的一種屬性，稱為「單調性」(Monotonicity)，「廣 義量詞理論」研究各種量詞的「單調性」。由於「所有」、「有」這些量詞有左、右兩個論元，每個論元可以 換成其真母集或真子集，相應地便有四種「單調性」。舉例說，我們可以定義「右遞增性」如下：設p和q為量 化句，我們說p的量詞是「右遞增」的當且僅當

類似地，我們也可定義「右遞減性」、「左遞增性」和「左遞減性」。據此，我們說量詞「有」是「左遞增、 右遞增」，而「所有」則是「左遞減、右遞增」的。

為清楚顯示量化句的內部結構，以下把量化句寫成「量詞(左論元)(右論元)」的標準形式，例如上面的(1)和 (2)便可分別寫成(下式略去副詞「在」和「都」)：

從集合論的角度看，我們可以把上式中的「小學生」和「跑步」看成兩個集合(這裡須把「跑步」理解為「跑步 者」的集合)，而量詞「有」和「所有」則是表達這兩個集合之間關係的「算子」(Operator)，其定義為：

即「有」表達一種「交集非空」關係，而「所有」則表達一種「子集」關係。

我們可以把「單調性推理」看成一種「梯級推理」，這是因為「子集-母集」可以構成一個「集合梯級」，例如 (1)的左論元便可構成如下「梯級」：

上述梯級構成一個「遞增」(即從小到大)的序列，序列中各項都是其右面各項的子集，而「單調性推理」的實 質就是把某一真「量化句」的論元換成該論元所處「梯級」上的其他元素後，所得語句是否仍然為真的推理。 「單調性推理」有豐富的內容，有興趣的讀者請參閱拙文《廣義量詞系列：單 調性推理原理》和《廣義量詞系列：單調性推理的擴展》。

3. 極性形容詞的單調性推理

3.1 基本概念

「極性形容詞」(Polar Adjective)是指可以用某種「度量」量度並以一對反義詞出現的形容詞，例 如如以「高度」作為「度量」，則有「高」和「矮」這對「極性形容詞」，其中「高」為「正向形容詞」 (Positive Adjective)，「矮」為「負向形容詞」(Negative Adjective)。至於如何界定何為「正」、何為「 負」，則要視乎形容詞與有關「度量」的正／反比例關係。舉例說，如果我們以「車速」作為「快／慢」的「 度量」，那麼由於「車速」與「快」成正比例關係，「快」和「慢」分別為「正向」和「負向」形容詞；但如 果我們以「車速」作為「安全／危險」的「度量」，那麼由於「車速」與「安全」成反比例關係，「安全」和 「危險」分別為「負向」和「正向」形容詞。

當代很多學者研究了「極性形容詞」的語義問題，提出了多種處理方案，本文採納Kennedy在On the Monotonicity of Polar Adjectives一文中的處理方案(略作修改)。Kennedy把「度量」表示為一條軸，並 區分軸上的兩種「範圍」(Extent)：「正向範圍」和「負向範圍」，前者為由軸的最低點到軸上某一點的範圍 ，後者為由軸上某一點到軸的最高點的範圍。利用上述概念，我們便可以用同一條軸表達「正向形容詞」和「 負向形容詞」的語義。試看下圖：

在上圖中，「6'5"」和「5'5"」為「高度」(以HEIGHT表示)軸上的兩點，每一點都把整條軸劃分為一個「正向 範圍」(帶下標「+」)和一個「負向範圍」(帶下標「−」)。此外，軸上還有兩點T和S分別代表「高」和 「矮」的某個標準，這兩個標準是參照「籃球員」(以BASKETBALL PLAYER表示)而定的，這是因為「極性形容詞 」的標準往往隨著被修飾的名詞而變化，例如「騎師」的高／矮標準便顯然有別於「籃球員」的標準。T和S也 分別把整條軸劃分為「正向範圍」和「負向範圍」，代表「高」、「不高」、「矮」和「不矮」這四個概念。 請注意由於「矮」相對於「高度」來說屬於「負向形容詞」，SHORT (BASKETBALL PLAYER)表現為一個「負向範 圍」。

根據上圖所述情況，以下兩句是真的：

現在如果我們把軸上的「範圍」看成集合，那麼我們可以把以上兩句表達為以下標準形式：

請注意在上式中，量詞「所有」的兩個論元必須同為「正向範圍」或「負向範圍」。使用上述表達法的優點是 ，我們可以利用量詞「所有」的「左遞減、右遞增」屬性來推導某些有趣的推理。舉例說，由於「騎師」(以 JOCKEY表示)的高度標準低於「籃球員」的高度標準而6呎7吋大於6呎5吋，我們有

利用(4)以及「所有」的「左遞減、右遞增」屬性，我們有以下推理：

Kennedy的理論還可以應用於「比較結構」，試看下圖：

上圖顯示兩個人－John和Mary的高度的「正向範圍」和「負向範圍」。利用上圖，可知以下推理是有效的：

我們可以把上述推理表達為以下標準形式：

請注意上述等價關係其實只是以下集合論定理的特例：

以上討論的推理都是顯而易見的，本文只是揭示這些日常推理背後的數學和語義學理據。

3.2 「太過」與「足夠」

Lobner在Phase Quantification: A Uniform Treatment of Some Quantifiers from Different Categories一文中討論了兩個副詞－「太過」("too")和「足夠」("enough")，並把這兩個詞的語義歸結為 某種量化現象。在本小節，筆者將使用Kennedy的理論框架表達Lobner的上述概念。我們可以把「太過」和「足 夠」表達為下圖中的「範圍」：

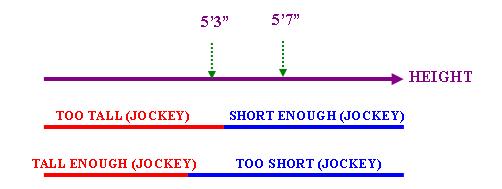
請注意上圖反映了Lobner提出的以下兩個相等關係(註2)：

參照上圖，我們可以使用上一小節介紹的方法來表達包含「太過」或「足夠」的語句。舉例說，以下兩句

便可以分別表達為(請注意根據上述相等關係，~TOO TALL (JOCKEY) = SHORT ENOUGH (JOCKEY)：

利用上式和量詞「所有」的「單調性」，容易得到以下推理：

此外，根據上圖，由於

我們亦有

3.3 廣義分式

以上討論的「極性形容詞」都只涉及一個「參項」(Parameter)，但在某些情況下，我們須考慮多個「參項」， 這時我們便要使用「分式」(Fraction)。舉例說，設我們使用完成工作件數(以JOB表示)、所需工人人數(以 WORKER表示)和完成工作所需日數(以DAY表示)這三個「參項」來衡量「有效率」(以EFFICIENT表示)這個「極性 形容詞」。那麼我們可以把EFFICIENT表達為下式：

請注意在上式中，JOB處於分子位置，這是因為JOB與EFFICIENT成正比例關係，而WORKER和DAY則處於分母位置 ，這是因為這兩個「參項」與EFFICIENT成反比例關係。利用上式和進行少許計算，我們便可得到以下推理：

在某些情況下，某些「極性形容詞」的「參項」並不以數值形式出現或不能進行計算。但即使如此，我們仍可 以對這些「極性形容詞」進行比較，在這種情況下，我們便要使用「廣義分式」(Generalized Fraction)的概念。設我們使用職級(以RANK表示)和達到某職級的年齡(以AGE表示)這兩個「參項」來衡量「叻」 (以SMART表示)這個粵語「極性形容詞」，其中RANK表現為以下梯級：

現在我們可以把SMART表達為以下「廣義分式」：

上式的理據是，一個人在越年輕時達到越高的職級便越「叻」。儘管我們不能對上式進行計算，但卻可比較兩 個分式之間的大小，關鍵是逐個「參項」進行比較，惟須注意位於分子和分母的「參項」在比較時有剛好相反 的方向，而且並非任何兩個「廣義分式」都可比較。舉例說，根據上式，我們有以下結果：

利用上面第一個結果，我們可得到以下推理：

在本小節，筆者引入了「廣義分式」的概念，這個概念其實只是某些「極性形容詞」與其「參項」的正／反比 例關係的濃縮表達式，以後讀者將會看到「廣義分式」在「梯級推理」中有很重要的作用。

4. 梯級隱涵

「隱涵」(Implicature)是Grice提出的概念，用來指語言中某些隱含的意思，亦即「言外之意」。Grice嘗試使 用一套「合作原則」(Cooperative Principle)及其下諸準則來把一般人在日常語言中表達和理解「言外之意」 的過程解釋為一種推理過程。後來，Horn發展了Grice的其中一條準則－「量準則」(Maxim of Quantity)，形 成「梯級隱涵」(Scalar Implicature)的理論。「梯級隱涵」的最顯著例子是以下推理：

上述推理是說，當某人說出「有小學生穿T恤」時，他實際隱含著「並非所有小學生都穿T恤」。上式中的下標 「P」代表上述推理是一種「語用推理」而非「邏輯推理」，「語用推理」的特點是可被取消，例如某人可以毫 不矛盾地說出以下這句：

現在讓我們看看語用學家如何解釋(5)的推導過程。首先，根據邏輯，對任何非空主語A和謂語B，均有

由此我們說，「所有」比「有」含有較高的「信息量」(Information Value)。我們可以把「所有」和「有」按 「信息量」從小到大排成以下「梯級」：

而Grice的「量準則」假設一個人在說話時會提供盡量多的信息，因此當一個人說出信息量較低的話語「有小學 生穿T恤」時，這意味著信息量較高的另一話語「所有小學生都穿T恤」不是真的，否則他便應說出後者而非前 者，由此得到(5)的推理。當然，上述「量準則」只是語用學家從日常語言中概括出來的一種常規，此一常規並 不總是成立，因此才有「梯級隱涵」的「可取消性」(Cancellability)。

我們可以把上述「梯級隱涵」推廣至否定的情況，這是因為對應於「肯定梯級」(6)，我們有以下「否定梯級」 ：

這個「梯級」告訴我們，「沒有」比「並非所有」含有較高的「信息量」，由此我們有以下「梯級隱涵」：

請注意從邏輯上說，「不是沒有」 = 「有」；不過從語用上說，兩者的語用功能略有不同，這裡不詳細討論。 繼Grice和Horn之後，其他學者(例如Levinson、Hirschberg等)還進一步擴展了「梯級隱涵」的理論，但由於他 們的理論涉及其他概念，本文不擬介紹。

現在讓我們總結一下以上介紹的內容。下圖列出「所有」("every")與「有」("some")之間推導 關係的各種可能性：

上圖使用「1」和「0」分別代表「真」和「假」，並且沿用邏輯學上常用的等式：~1 = 0和~0 = 1。在上圖左 面四個箭頭中，綠色實線和紫色虛線的箭頭分別代表有效的「邏輯蘊涵」(Logical Entailment)和「梯級隱涵」 。根據上圖，我們可以把「邏輯蘊涵」重新理解為：從信息量較高的真(假)命題必然地推出信息量較低的真 (假)命題；而梯級隱涵則是從信息量較低的真(假)命題推出信息量較高的真(假)命題的否定。

此外，上圖右面還有四個箭頭，其中紅色帶「×」號的箭頭代表完全違反邏輯的無效推導，例如從「所有 小學生都穿T恤」推出「沒有小學生穿T恤」便是不合邏輯的。藍色的箭頭則代表一種具有或然性的推導(這種推 導其實還要加上一個條件：截至說話時刻為止，並未觀察到使~every為真的事例)，例如從「有小學生 穿T恤」(加上以下條件：「截至說話時刻為止，並未觀察到有小學生不穿T恤」)，我們只能或然性地推出「所 有小學生都穿T恤」。由此可見，這最後一種推導其實就是現代邏輯學上的「歸納推理」(Inductive Reasoning)，即從「部分」推出「全部」的推理。由於「歸納推理」與本文的研究範圍並無直接關係，本文不 擬深入討論這種推理。

5. 梯級算子

5.1 基本概念

「梯級算子」(Scalar Operator)是指那些其語義涉及「梯級推理」的詞項。有關「梯級算子」的理 論是較近期才發展起來的，因此學界對「梯級算子」尚未有全面的研究，只有"even"(相當於漢語的「連／甚至 」)和"let alone / not to mention"(相當於漢語的「何況／別說」)有較系統的研究，本節將集中討論這兩個 詞項，並採用Kay在Even以及Fillmore等人在Regularity and Idiomaticity in Grammatical Constructions: The Case of Let Alone一文中提出的「梯級模型」(Scalar Model)作為分析框 架。

「梯級模型」是由一些具有相同「參項」的語句排成的陣列，現以以下命題函項為例說明「梯級模型」的概念 ：

上式包含兩個「參項」：代表「跳高選手」的JUMPER和代表「障礙」的OBSTACLE。現假設JUMPER的成員按其「 笨拙度」從低到高排成一個「梯級」，而OBSTACLE的成員則按其「難度」從低到高排成另一個「梯級」，這兩 個「梯級」共同構成一個二維陣列，如下圖所示：

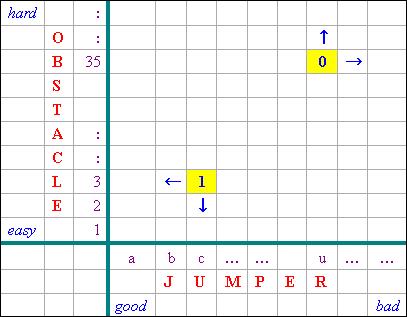
上圖中的每一個方格代表把JUMPER和OBSTACLE的成員代入(8)的兩個「參項」後所得的命題，1和0為該命題的真 值。以下把上圖中的每一個方格記作有序對(x, y)(例如上圖中標有「1」的黃色方格便可以記作(c, 3))，並且 把x和y分別稱為x坐標和y坐標。請注意上述「梯級模型」具有以下「梯級屬性」(Scalar Property)：

上述屬性其實反映了以下「梯級推理」(以下假設「豬肉榮」較「鬼腳七」笨拙，「3號障礙」較「2號障礙」難 )：

請注意上述推理只考慮了「選手笨拙度」和「障礙難度」這兩個因素，因此只有當「其他因素等同」(other things being equal)時，上述推理才成立。舉例說，一個跳高能力強的選手完全有可能因運氣、心情或其他因 素而跳不過比他差的選手所跳得過的障礙。

為了刻劃上述兩個「梯級算子」的語義，我們還需引入兩個概念：「文本命題」(Text Proposition，簡稱tp) 和「語境命題」(Context Proposition，簡稱cp)，前者是指含有「梯級算子」的語句在減去該「梯級算子」後 所得的命題，後者則是指存在或隱含於語境中與tp形成對比的另一命題(略去某些表達語氣的詞語)。例如在語 句

中，

請注意在上句中，cp被置於括弧中，這表示cp不一定要在實際說話中出現，而可以潛在於語境中。以下是Kay、 Fillmore等人總結出的「連／甚至」和「何況／別說」這兩個詞項的「恰當性條件」(Felicity Condition)(註 3)：

根據以上條件，可知「連」和「何況」的使用在以下兩句中是恰當的：

5.2 LIKELIHOOD函項

上述對「梯級算子」的分析無疑是很成功的，不過筆者認為我們還可以進一步把上述分析表達為「廣義分式」 的形式，從而把「梯級算子」的推理與「單調性推理」聯繫起來。首先，「梯級模型」上的命題可以看成為按 照「可能性」(Likelihood)排列，離原點越近的命題，其可能性越大，例如笨拙度最低的選手跳得過難度最低 的障礙，這是可能性最高的。換句話說，JUMPER的「笨拙度」和OBSTACLE的「難度」與(8)的「可能性」成反比 例關係，據此我們可以定義以下的LIKELIHOOD函項(註4)：

請注意我們可以從上式容易得到LIKELIHOOD("JUMPER跳不過OBSTACLE")的公式，只需把上式中的分子和分母對 調便行了。

我們還須把前述的「梯級屬性」(9)重新表達為LIKELIHOOD函項的屬性。這並不困難，因為我們可以把 LIKELIHOOD看成「極性形容詞」"likely"的度量，試看下圖：

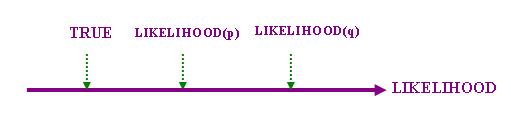
為簡化討論，上圖只標出LIKELIHOOD軸上的三個刻度而沒有繪出相應的「正／負向範圍」。上圖中的TRUE代表 在語境中的某個「真」的標準，所有LIKELIHOOD值達到或超過這個標準的命題都是真的。利用上圖，我們可以 把「梯級屬性」(9)重新表述為：設p、q為同一「梯級模型」中的命題，那麼

請注意(13)與前面第1節的「右遞增性」定義(3)具有非常相似的形式，由此可見「梯級屬性」與「單調性推理 」有密切的關係。我們也可以把前述的語用推理重新表述為

當然，最重要的是我們可以把前述的兩個「恰當性條件」(10)和(11)也重新表述為以下形式：

從以上兩式可見，「連／甚至」的作用就是透過確定一個可能性較cp低的tp來表達某種「意料之外」的意思， 這一點正符合很多學者對「連／甚至」的語義分析。讀者可自行把適當的元素代入(12)中的「參項」，並驗證 上述「梯級屬性」、推理和「恰當性條件」與上一小節討論的情況完全吻合。

6. 極大／極小詞

Israel在Polarity Sensitivity as Lexical Semantics一文中把「梯級模型」應用於「極性敏感詞」 (Polarity Sensitive Item)(即只能出現於肯定語境或否定語境的詞項)，用以解釋這些詞項的語法、語義、語 用、修辭問題。Israel的理論是有用和有系統的，但筆者認為「極性敏感詞」牽涉複雜的問題，使用Israel的 理論框架仍不能解釋很多現象；不過，如果我們把他的理論應用於「極大詞」(Maximizer)和「 極小詞」(Minimizer)，卻能解釋很多有趣的「修辭推理」(Rhetorical Reasoning)現象。事實上， Israel在後來的另一篇論文Minimizers, Maximizers and the Rhetoric of Scalar Reasoning中，便 已把注意力轉移到「極大詞」、「極小詞」和「修辭推理」方面。

「極大詞」和「極小詞」是指那些表達極大或極小數量，主要用於修辭的詞項，例如漢語的「百毒」、「一毛」 等。這些詞項的修辭功能大致上可分為「增強」(Emphatic)和「減弱」(Attenuating)兩種，以下筆者將改進 Israel的理論，分析這些詞項的這兩種修辭功能。以下把用於「增強」和「減弱」功能的「極大／極小詞」分 別稱為「增強型極大／極小詞」和「減弱型極大／極小詞」，請注意本文並不否定同一個詞項既可用於「增強」 功能，又可用於「減弱」功能。

6.1 增強型極大／極小詞

「增強型極大／極小詞」可用來加強句子的語氣，或達致誇張的效果，例如以下兩句中的「使鬼推磨」和「草木」：

我們沿用上一節介紹的LIKELIHOOD函項分析以上兩句的「恰當性條件」。首先考慮(16)，我們把該句抽象為以 下命題函項並以之構成一個一維的「梯級模型」：

在上式中，DIFFICULTY代表事情的難度。由於DIFFICULTY與上句的「可能性」成反比(難度越大便越不可能達成 )，我們可以定義以下函項：

由於「使鬼推磨」是難度極高的事情，把此一「參項值」代入上式中的DIFFICULTY，所得LIKELIHOOD的值將會 極低。根據前述的「梯級屬性」(13)，如果一個「可能性」極低的命題為真，那麼同一「梯級模型」內的幾乎 所有命題都為真，因此(16)實際上是要表達以下意思：

其次考慮(17)，我們把該句抽象為以下命題函項並以之構成另一個「梯級模型」：

在上式中，LIVELINESS代表事物的「生命度」。由於LIVELINESS與上句的「可能性」成正比(生命度越大的事物 越可能被驚慌的逃難者誤會為兵)，我們可以定義以下函項：

由於「草木」是生命度極低的事物，把此一「參項值」代入上式中的LIVELINESS，所得LIKELIHOOD的值將會極 低，根據類似推理，我們推知(17)實際上是要表達以下意思：

總結以上討論，我們可以把「肯定式增強型極大／極小詞」的「恰當性條件」確定為(在以下條件中，p為包含 「增強型極大／極小詞」的命題)：

請注意儘管(16)和(17)中的「使鬼推磨」和「草木」分別表達極大量和極小量，但由於DIFFICULTY和 LIVELINESS在相關的LIKELIHOOD函項中分別處於分母和分子位置，所以兩者都造成「LIKELIHOOD(p)極小」的結 果(註6)。

以上討論了肯定句，現在讓我們考慮否定句。試看以下例句：

請注意這裡應把「一毛」理解為「至少一毛」(註7)。我們首先把以上兩句轉化為相應的肯定句，然後把它們的 LIKELIHOOD函項定為

上述公式的理據是：金額(AMOUNT)越大，越難付出(反比例)；毒的數量(QUANTITY)越大，越容易侵襲人體(正比 例)。把極小的「一毛」和極大的「百」代入上式，便得到「LIKELIHOOD(p)極大」的結果。根據「梯級屬性」 (13)，如果一個「可能性」極高的命題為假，那麼同一「梯級模型」內的幾乎所有命題都為假，因此(19)和 (20)實際上是要表達以下意思：

總結以上討論，我們可以把「否定式增強型極大／極小詞」的「恰當性條件」確定為(在以下條件中，p為轉化 為肯定式後的命題)：

(18)和(21)反映了以下修辭策略：透過肯定一個可能性極低的語句或否定一個可能性極高的語句來達到加強語 氣或誇張的效果。

6.2 減弱型極大／極小詞

「極大／極小詞」亦可用來減弱句子的語氣，使說話留有餘地。與「增強」功能相比，「極大／極小詞」的「 減弱」功能較難分析，因為我們不能應用「梯級屬性」(13)對「減弱型」的語句作出邏輯推理。但筆者認為， 我們可以應用第4節介紹的「梯級隱涵」作出一些推導。先看以下肯定句：

沿用上文的分析框架，我們可以把上句的LIKELIHOOD函項定為：

其中DEGREE代表某人作出貢獻的程度，這個參項構成以下梯級：

把上述梯級中的極小項「有所」代入上面的LIKELIHOOD函項，所得函項輸出值將會極高。換句話說，(22)是一 個可能性極高的命題，因此具有極低的信息量。根據梯級隱涵的理論，一個信息量極低的肯定命題隱涵同一梯 級模型中另一個信息量極高的肯定命題的否定，因此(22)隱含著以下意思：

這說明了為何「有所」經常被用來減弱語氣，使說話留有餘地。總結以上討論，我們可以把「肯定式減弱型極 大／極小詞」的恰當性條件確定為：

其次考慮以下否定句：

把上句轉化為相應的中性肯定句並把「全」改為QUANTITY後，便得到命題函項「出QUANTITY力」，因此(24)的 LIKELIHOOD函項跟(22)的相同。把極大的「全」代入QUANTITY，所得LIKELIHOOD的值將會極低，亦即「盡全力 」的「信息量」極高。根據「梯級隱涵」的理論，否定一個「信息量」極高的命題隱含著否定同一「梯級模型 」中另一個「信息量」極低的命題的否定，因此(24)隱含著以下意思：

上述分析說明了為何(24)可用來減弱否定語氣，使說話留有餘地。總結以上討論，我們可以把「否定式減弱型 極大／極小詞」的「恰當性條件」確定為：

當然，由於「梯級隱涵」具有「可取消性」，上述分析結果不是放諸四海而皆準的。舉例說，在某些語境下， 「未盡全力」便可能含有較多責怪意味、較少留有餘地的意思。

下圖列出「增強型極大／極小詞」與「減弱型極大／極小詞」的各種可能「修辭推理」關係：

請注意上圖跟第4節的圖非常相似，這說明本文介紹的「修辭推理」與經典的「邏輯蘊涵」和「梯級隱涵」有相 通之處。上圖左面四個箭頭中，綠色實線和紫色虛線的箭頭分別代表「增強型極大／極小詞」和「減弱型極大 ／極小詞」的「修辭推理」，而右面的紅色和藍色箭頭則分別代表完全違反邏輯的無效推導和並無必然性的「 歸納推理」。其中藍色的箭頭告訴我們，修辭也須遵循某些規律，違反這些規律便達不到理想的修辭效果，例 如

便難以表達「有錢能做任何事情」的意思。

7. 主觀量副詞

7.1 基本概念

「主觀量」(Subjective Quantity)是近十多年才發展起來的漢語語法學課題。由於「主觀量」此一 概念為我們提供了解釋漢語某些虛詞語義的全新視角，因此頗引人注目。請看以下語句：

上面第一句只是客觀地陳述一個量(「三天」)，該句所表達的是「客觀量」(Objective Quantity)。與第一句 不同 ，第二和第三句則包含對量的大小的主觀評價，這種主觀評價是透過副詞「才」和「都」分別表達上述「 天數」為小量和大量，因此該兩句所表達的是「主觀量」。根據李善熙的博士論文《漢語"主觀量"的表達研究》 ，漢語用來表達「主觀量」的方法紛繁多樣，包括語音手段、詞綴、複疊以及各種詞匯，本文不可能一一細述 ，只擬集中討論「才」、「都」等幾個常用「主觀量副詞」。

李宇明在《漢語量範疇研究》一書中提出了「主觀量」的幾種類型，其中「異態型主觀量」與本文的主題有最 直接的關係，因此本文將主要討論「異態型主觀量」。「異態型主觀量」是相對於「期待量」而言的(註8)，「 期待量」是指說話者心目中預期的量，這個量可以實際出現於說話中，也可以隱含於語境中。當說話者談論的 量有別於「期待量」時，便會產生「異態型主觀量」。請注意上述概念正好與前面第5節介紹的cp、tp概念相通 ，所以筆者將沿用這兩個概念。以下把包含「異態型主觀量」的語句在減去「主觀量副詞」後所得的語句稱為 tp，把包含「期待量」的語句(略去某些表達語氣的詞語)稱為cp。例如在語句

中，

由於上面tp中的量(「三天」)少於cp中的量(「一星期」)，所以說話者使用「才」來表達「主觀小量」。

除了「異態型主觀量」外，李宇明還提出「感染型主觀量」的概念。試看以下例句：

在上句中，「才」標誌著其後的「一萬元」是「主觀小量」；「兩個人」本來沒有主觀性，但相對於「一萬元」 來說，卻有著「大量」的意味，因此李宇明說「兩個人」被感染成「主觀大量」。筆者認為這句其實反映了一 個比例的問題，如果我們把這句的量看成「平均收入」(以AVERAGE-INCOME表示)，那麼這個量與「賺錢人數」 (以PERSON表示)和「收入總數」(以TOTAL-INCOME表示)的關係可用下式表達：

上式顯示TOTAL-INCOME與PERSON成反比例關係，因此當「一萬元」具有「主觀小量」時，「兩個人」相對地便 具有「主觀大量」的意味。由於以下筆者將廣泛採用「廣義分式」來表達一句中多個數量詞語之間的關係，我 們無須區分「異態型主觀量」和「感染型主觀量」。

7.2 「就／便」與「才／只」

漢語副詞所能出現的位置紛繁複雜，為簡化討論，以下只集中討論在一種「標準」句式下的「主觀量副詞」， 這種句式就是「主觀量副詞」出現於謂語前的狀語位置。在這種句式中，「主觀量副詞」的左側和右側均可能 出現數量詞語，以下把這些詞語分別記作Q_l和Q_r，其中下標"l"和"r"分別代表「左」 和「右」。接著我們仿照前面第5節的做法，定義一個LARGENESS函項，以表示語句所表達數量的大小。舉例說 ，如果我們把語句(27)抽象為命題函項「Q_l人賺Q_r」，那麼我們可以把LARGENESS定 為

請注意上述「廣義分式」不僅適用於「Q_l人賺Q_r」此一句式，而是有普遍適用性，這 是因為處於「主觀量副詞」右側的數量詞語Q_r是句意的重點，而處於「主觀量副詞」左側的數量詞 語Q_l則起著與Q_r相對比的作用，與Q_r成反比例關係。因此我們可以把上式 推廣為以下一般形式：

利用上述函項，我們便可以把某些常用「主觀量副詞」的「恰當性條件」定為(註9)：

根據以上「恰當性條件」，我們可知以下兩句中「就」和「才」的使用是恰當的(以下例句中括弧的部分代表cp )：

「恰當性條件」(29)和(30)不僅適用於包含兩個數量詞語的句子(李宇明稱為「雙量式」)，還適用於只包含一 個數量詞語的句子(李宇明稱為「單量式」)和包含多個數量詞語的句子(以下稱為「多量式」)。首先考慮「單 量式」，如果我們採取廣義的觀點，把「梯級」也看成「量」，那麼某些表面上是「單量式」的句子也可被處 理成「雙量式」。試看以下句子：

我們可以根據(28)把上句的LARGENESS函項定為

其中Q_r代表以下梯級：

應用「廣義分式」的比較方法，容易看到(31)中「就」的使用是恰當的。

對於那些真正只含一個數量詞語的「單量式」，我們可以把沒有出現的數量詞語Q_l或 Q_r當作1。以(26)為例，我們可以把該句的LARGENESS函項定為

利用上式，容易看到(26)中「才」的使用是恰當的。

其次考慮「多量式」，我們可以把這些句子中出現於「主觀量副詞」左側或右側的多個數量詞語處理成「廣義 分式」中分母或分子上的乘積。試看以下句子：

在上句的tp中，「只」的左側有兩個數量詞語(以下記作Q_l1、Q_l2)，右側有一個數量 詞語(記作Q_r)，根據以上討論，我們可以把上句的LARGENESS函項定為

利用上式，容易看到(32)中「只」的使用是恰當的。

7.3 「都」與「還」

在李宇明著重研究的「主觀量副詞」中，「都」與「還」的情況較為特殊，因為在判斷這兩個詞的「恰當性」 時，我們不能光看句子中數量詞語相對於這兩個副詞的位置，而要看這些數量詞語與全句謂語的可能性的正／ 反比例關係，由此可見「都」與「還」與前面第5節討論的「連／甚至」很相似，都可以看作「梯級算子」。事 實上，如前所述，「連／甚至」是透過確定一個可能性較低的語句來表達某種「意料之外」的意思，而根據 《實用現代漢語語法》，「還」正好包含「意料之外」此一語義。此外，根據張亞軍的《「連」字結構的歷史 發展與「都」的功能演變》一文，「都」最初與「連」一起構成「連...都」結構，後來「連」逐漸虛化，變得 可有可無，「都」便承載了原來由整個「連...都」結構表達的意義，由此可見「都」在某些意義上與「連」根 本是相通的。

至於「都」與「還」何以能表達「主觀量」，這正與它們所表達的「意料之外」意思有關。如前所述，「異態 型主觀量」的成因是說話者談論的量與某種「期待量」出現差異，亦即說話者談論的量是一種「意料之外」的 量。由此可見，「都」與「還」所表達的「主觀量」其實是其「意料之外」意義的「副產品」，是一種「非典 型主觀量副詞」，因此它們的「恰當性條件」有別於「就／便」與「才／只」這類「典型主觀量副詞」。

基於以上討論，我們現在可以把「都」與「還」的「恰當性條件」確定為：

以下讓我們看上述「恰當性條件」的應用實例。首先考慮「都」，「都」可以出現於「單量式」和「雙量式」 中，但在出現於「單量式」時用法頗為複雜多樣，為簡化討論，以下暫只考慮形如「Q_l + 都 + 謂 語」的「單量式」。試看以下例句(註10)：

在「單量式」(34)中，由於重量(以WEIGHT表示)越大便越可能覺得累，所以WEIGHT與全句的謂語「覺得累」成 正比。在「雙量式」(35)中，由於時間(以TIME表示)越長越不可能做不完一定數目的題目，而題目(以 QUESTION表示)越多越可能做不完，所以TIME和QUESTION與全句的謂語「做不完」分別成反比和正比。根據上述 分析，我們可以把以上兩句的LIKELIHOOD函項分別定為

利用上述函項和「恰當性條件」(33)，我們便可推知「都」在(34)和(35)中的使用是恰當的。

「還」的情況跟「都」類似，不過「還」常常出現於疑問句中。試看以下例句：

在「雙量式」(36)中，由於錢(以MONEY表示)越多便越買得起一件商品，而牛仔褲的數量(以QUANTITY表示)越大 便越難買得起，所以MONEY和QUANTITY與全句的謂語「買得起」分別成正比和反比。在「單量式」(37)中，由於 價錢(以PRICE表示)越高便越難買得起，所以PRICE與全句的謂語「買得起」成反比。根據上述分析，我們可以 把以上兩句的LIKELIHOOD函項分別定為

利用上述函項和「恰當性條件」(33)，我們便可推知「還」在(36)和(37)中的使用是恰當的。

請注意「都／還」的情況與前面第6節介紹的「極大／極小詞」有點類似，儘管與「都／還」共現的數量詞語與 這兩個副詞可以成正比／反比關係，但我們可以用同一個「恰當性條件」(33)概括各種情況，這就是本文採用 「廣義分式」的優點。

8. 各種複合形式

8.1 梯級算子與極大／極小詞的複合

在第5至7節，筆者介紹了各種「梯級算子」、「極大／極小詞」和「主觀量副詞」的「恰當性條件」。這些詞 項不是孤立的，而是可以共現於同一句中，以下筆者簡介一些常見的複合形式並解釋其理據。為方便以下的討 論，現先把某些「梯級算子」和「極大／極小詞」的「恰當性條件」重列於下：

首先，從(14)和(15)可見，在「連／甚至」與「何況／別說」的「恰當性條件」中，tp與cp的比較關係具有相 反方向，因此在自然語言句子中，這兩個詞常可共現於同一個複句中，如下句所示：

請注意在上句中，「豬肉榮跳得過3號障礙」與「鬼腳七跳得過3號障礙」互為對方的cp。

其次，從(14)和(18)可見，「連／甚至」與「肯定式增強型極大／極小詞」的「恰當性條件」相容，因為如果 LIKELIHOOD(p)極小，那麼LIKELIHOOD(p)自然少於任何cp的LIKELIHOOD值，因此「連／甚至」一般可以與「肯 定式增強型極大／極小詞」共現。不過，由於「極大／極小詞」有很強的習語性質，它們不能任意加插詞項， 在與「連／甚至」共現時可能須把原來的語句大幅改寫才行，例如「草木皆兵」便要改寫為

同理，從(15)和(23)亦可見「何況／別說」與「肯定式減弱型極大／極小詞」在理論上可以共現。不過，正如 筆者在6.2小節中指出的，「減弱型極大／極小詞」的「梯級推理」具有「可取消性」，不是總是成立的。而且 由於「極大／極小詞」的習語性質，這些詞項與「何況／別說」共現的例子便更少見，以下是筆者自擬的例句 ：

8.2 框式主觀量副詞

在本小節我們討論「框式主觀量副詞」，即由「主觀量副詞」自身或與「梯級算子」、「極大／極小詞」組成 的框架。首先，第7節介紹的「主觀量副詞」往往可以互相組成一些框架，例如「只...就...」、「才...就... 」、「只...還...」、「才...還...」等。有趣的是，這些框架中最後一個副詞的「恰當性條件」就是整個「 框式主觀量副詞」的「恰當性條件」。換句話說，「框式主觀量副詞」所表達的「主觀量」由最後一個副詞決 定，其他副詞退居次要地位。舉例說，以下語句

的「恰當性條件」便等於「就」的「恰當性條件」，即

其中

讀者可自行驗證在上句中「只...就...」的使用是恰當的。

筆者在7.3小節沒有考慮形如「都 + (謂語) + Q_r」的句式，這是因為這類句式較難分析，其中的 「謂語」常可省去，例如

現在如果我們把這類句式看成隱含著某種「框式主觀量副詞」，便使分析變得較容易。事實上，上述句子不能 單獨成句，要在其後補上一句語義才能完整，例如下句：

這樣我們便把(38)改寫成包含「都...還...」的句子。根據前面的討論，這個框架的「恰當性條件」由其最後 一個副詞「還」決定，即

其中

上式的理據是，年紀越大(這裡只考慮完成發育之前的年齡)，越能挑得起重物；物件越重，越挑不起。讀者可 自行驗證在上句中「都...還...」的使用是恰當的。

其次，某些「主觀量副詞」可以與「梯級算子」組成框架，最常見的格式是「連／甚至...都／也...」。如前 所述，「連／甚至」與「都」在某些意義上是相通的，因此兩者經常同現，例句如：

此外，根據前述「連／甚至」與「何況／別說」的共現關係，我們還可以進一步得到更複雜的框架「連／甚至 ...都／也...何況／別說...」，例句如：

9. 單調性概念的推廣

9.1 恰當性算子的單調性

我們首先回顧「連／甚至」的「恰當性條件」：

從上式容易看到，如果我們把tp換成另一個LIKELIHOOD值更低的真命題tp'，那麼上述條件必然成立。舉例說， 設我們沿用第5節的例子，由於

如果「連／甚至豬肉榮都跳得過2號障礙」是恰當的，並且豬肉榮也跳得過3號障礙，那麼根據(14)，「連／甚 至豬肉榮都跳得過3號障礙」必然也是恰當的。上述結果不是偶然的，而是從「連／甚至」的「恰當性條件」導 出的必然結果，因此我們可以把「連／甚至」的「恰當性條件」改寫為(在以下條件中，p和q為命題)：

在上式中，「連／甚至」被寫成「算子」的形式(例如句子「連／甚至豬肉榮都跳得過3號障礙」可以被寫成「 連／甚至(豬肉榮跳得過3號障礙)」)，筆者把這種算子稱為「恰當性算子」(Felicity Operator)， 因為對於這些算子，我們關心的不是「真值條件」，而是「恰當性條件」(除了「連／甚至」和「何況／別說」 外，「極大／極小詞」和「主觀量副詞」也可被看成「恰當性算子」)。此外，請注意(39)跟以下量詞的「遞減 性」定義非常相似(在以下定義中，p和q為量化句)：

由此我們可以把量詞的「單調性」概念擴大至「連／甚至」這類「恰當性算子」，並把「連／甚至」看成「關 於LIKELIHOOD函項的遞減算子」。同理，我們亦可以把「何況／別說」看成「關於LIKELIHOOD函項的遞增算子」 。

上述概念還可以推廣至「主觀量副詞」。舉例說，「就／便」的「恰當性條件」便可以改寫為：

上述條件告訴我們，如果「我們兩個人就賺了一萬元」是恰當的，並且「他們」兩個人賺了二萬元，那麼「他 們兩個人就賺了二萬元」也是恰當的。請注意(41)跟量詞「遞增性」的定義非常相似，由此我們可以把「就／ 便」看成「關於LARGENESS函項的遞增算子」。同理，我們亦可以把「才／只」看成「關於LARGENESS函項的遞 減算子」以及把「都／還」看成「關於LIKELIHOOD函項的遞減算子」。

9.2 蘊涵梯級與恰當性梯級

在上一小節，筆者提出了「恰當性算子」的「單調性」概念，並指出此一概念與「量詞」的「單調性」概念有 密切的聯繫。其實，我們還可以從另一角度看「恰當性算子」與「量詞」之間的聯繫。為此，筆者首先提出 「蘊涵梯級」(Entailment Scale)的概念。一個「蘊涵梯級」就是由一組有相似語義內容和句法結構 的命題組成的梯級，梯級內的每一項蘊涵其右面各項，即如果某一項是真的，那麼其右面各項也是真的。舉例 說，根據「量化句」的「單調性推理」，我們可以構造以下「蘊涵梯級」：

類似地，我們亦可以定義「恰當性梯級」(Felicity Scale)，即由一個「梯級模型」內的命題組成的 梯級，在這梯級中，如果某一項是恰當的，那麼其右面各項只要是真的也都是恰當的。舉例說，利用第5節的「 梯級模型」，我們可以構造以下帶「連」的「恰當性梯級」：

上述概念還可以推廣至「主觀量副詞」。舉例說，沿用上一小節的例子，我們可以構造以下帶「就」的「恰當 性梯級」：

最後，讓我們考慮「極大／極小詞」。由於「極大／極小詞」一般具有習語性質，而且其語義和「恰當性條件」 都是有關極端情況，我們難以構造「極大／極小詞」的「恰當性梯級」。舉例說，我們不能從「一毛不拔」的 恰當性推出「半毛不拔」的恰當性，因為漢語中壓根兒沒有「半毛不拔」此一成語。即使同時存在兩個有數量 差距的「極大／極小詞」，我們也不能說其中一個比另一個更恰當。舉例說，儘管漢語有「寸步不讓」和「半 步不讓」這兩種說法，我們卻不能把這兩個「極小詞」排成「恰當性梯級」，只能說它們具有相同等級的恰當 性。

10. 總結

在本文中，筆者透過「梯級」、「廣義分式」、「單調性」等概念對「量詞」、「極性形容詞」、「梯級算子」 、「極大／極小詞」、「主觀量副詞」等進行了統一處理，所涉及的範圍橫跨語義學、語用學、修辭學、語法 學等領域，揭示了「梯級推理」在日常語言中的普遍性。從更廣的角度看，「梯級」的概念其實體現了數學上 「序」(Order)的概念，而「序」結構正是當代數學研究的三大結構(代數結構、序結構、拓樸結構)之一，由此 可見「梯級」概念在人類思維中的普遍性和重要性。

必須指出的是，本文涉及的某些課題是近期才提出來的，還在發展之中，因此本文只觸及這些課題的某個側面 ，遠遠談不上全面剖析。以「主觀量副詞」為例，這些詞項有很豐富的語義和複雜的用法，例如「才」可用來 表達時間關係，「都」則可用來表達總括，具有類似於「全稱量詞」的作用，等等。本文只是把「主觀量」與 「梯級推理」結合，從而討論這些詞項語義中的某個側面，如何把本文的框架推廣至其他側面，還有待深入研 究。不過，筆者相信本文已指出進一步研究上述課題的可行方向。

刊載本文的網頁

• 思想者-思想俱樂部

返回語言學專題