
筆者在《廣義量詞系列:單調性推理原理》中介紹了「單調性推理」的概
念,並總結出「單調性推理原理」。在該網頁中,筆者所討論的量詞全都是「<1,1>型量詞」(註1)。可是筆者
以往還介紹了多種其他類型的量詞和量化結構,一個自然的問題是,「單調性推理原理」是否也適用於這些量
詞和量化結構?本文將嘗試解答這個問題。
正如「<1,1>型量詞」包含著「模糊量詞」和「疑問量詞」等次類一樣,其他量詞和量化結構也包含著相應的次
類。不過,由於「模糊量詞」和「疑問量詞」涉及「隸屬度函數」和「可能世界集合」等複雜概念,為免使討
論過於複雜,本文將避免以這兩類量詞作為討論或舉例的對象。
我們首先從論元結構較「<1,1>型量詞」更簡單的「<−,1>型量詞」說起,這類量詞儘管也可以表達為「
三分結構」Q(A)(B)的形式,但它們的其中一個論元沒有真子集或真母集,因而只有「左/右單調性」。這類量
詞又可細分為「光桿名詞短語」和「第一類泛化量化結構」,本小節首先討論前者。
筆者在《廣義量詞系列:基本單式量詞》中介紹了三種「光桿名詞短語」:
「專有名詞」、光桿「類名詞」和光桿「抽象名詞」。這些名詞短語在表面上不含任何量詞,但其實隱含著全
稱語義,都可表達為「every(A)(B)」的形式,其中A為「單元集」(註2),例如「John是學生」便可表
達為
根據上式,可以推知這類量化結構應像"every"那樣具有「右遞增性」。不過,由於這類量化結構的左 論元A是「單元集」,沒有非空真子集,因此這類結構無「左單調性」可言。根據以上討論,我們有以下有效推 理:
筆者在《廣義量詞系列:時間量化結構》中介紹了兩類「泛化量化結構」, 「第一類泛化量化結構」的抽象形式為Q(U)(B),其中U代表「論域」。這類結構中的量詞都是「<−,1>型 量詞」,例如"everything"、"(nobody except John)"等。由於這類結構的左論元U相當於一個 常項,這類結構無「左單調性」可言。至於「右單調性」,則與相關的「<1,1>型量詞」的「右單調性」相同, 例如"everything"和"somebody"分別跟"all"和"some"一樣具有「右遞增性」; "nothing"跟"no"一樣具有「右遞減性」,而"(everything except God)"和 "(nobody except John)"則分別跟"(all except John)"和"(no except John)"一樣具 有「右非單調性」。以下是上述結構的一些有效及無效推理的實例:
「第二類泛化量化結構」是指英語的「存在句」,其抽象形式為Q(A)(U)。這類結構中的量詞可以是各式各樣的 量詞,最常見的是「<1,1>型量詞」。由於這類結構的右論元是論域U,這類結構無「右單調性」可言,但仍有 「左單調性」,此即結構中的量詞Q的「左單調性」。以下是這類結構的一些有效及無效推理的實例:
如前所述,「第二類泛化量化結構」中的量詞也可以是其他量詞。特別地,如果我們是以"something" 、 "nothing"等作為這類結構中的量詞(從而構成「第一、二類混合泛化量化結構」)的話, 那麼所得結構的抽象格式將為Q(U)(U),即兩個論元都沒有「單調性」可言,我們將無法進行任何「單調性推理 」:
不過,如果這類結構帶有「後續成分」,那麼由於這個「後續成分」可以有真母集或真子集,我們仍可以談論 這類結構的「單調性」,例見以下推理:
筆者在《廣義量詞系列:基本單式量詞》中介紹了三類「結構化量詞」,由 於這類量詞包含兩個以上的論元,我們不能再用「左」/「右」來標示這些論元,而必須把這些論元稱為「第1 論元」、「第2論元」...。相應地,我們也需要更一般的「單調性」定義。設有一個「n位量詞」 Q(A1, ... An),我們說Q是「第k論元遞增」(Increasing in the kth Argument)的當且僅當對所有集合A1, ... Ak, Ak', ... An 而言,若Ak ⊆ Ak',則有
至於「第k論元遞減」(Decreasing in the kth Argument)、「第k論元非單調」 (Non-Monotone in the kth Argument)等概念,也可作出相應定義。以下筆者將考察各類「結構化量詞」的「 單調性」,在以下的討論中,筆者將要多次使用以下定理(證明從略):
| 定理1: | 設A ⊆ B,則對任何集合C而言, | |
| (1) | |C ∩ A| ≤ |C ∩ B| | |
| (2) | C ∩ A ⊆ C ∩ B | |
| (3) | C ∪ A ⊆ C ∪ B | |
第一類「結構化量詞」是指包含兩個以上論元的「數量比較詞」,這類量詞可體現為<12,1>、
<1,12>和<12,12>這三種論元結構。由於在這三種結構中,
<12,12>型是最複雜的,而且其餘兩種可被視為第三種的特例,以下將主要討論
「<12,12>型結構化量詞」的「單調性」,其餘兩種結構類型的「單調性」可從這種結
構類型的「單調性」推導出來。
首先考察「<12,12>型量詞」"(more ... than ...)"的「單調性」,這個量詞
的真值條件為
根據上式,容易看到論元A是「遞增」的,這是因為若A ⊆ A',則根據「定理1(1)」,有|A' ∩ C| ≥ |A ∩ C|,因此
同理亦容易推斷其他論元的「單調性」。由於C跟A一樣位於(1)中「>」號的左方(以下稱為「多」方),這個論
元也應跟A一樣具有「遞增性」。反之,由於B和D位於(1)中「>」號的右方(以下稱為「少」方),這兩個論元應
具有「遞減性」。總括而言,上述量詞是「第1、3論元遞增,第2、4論元遞減」的。
接著考察「<12,1>型量詞」"(more ... than ...)"的「單調性」,這個量詞的真值條件為
跟(1)比較,上式中的A和B的位置不變,因此這兩個論元的「單調性」同前;但在上式中C的位置卻很特殊,它 同時出現於「多」方和「少」方中,由此可以推斷這個論元很可能是「非單調」的。事實上,不難找出一些反 例以證明C的「非單調性」。試看下圖:

在上圖中,C'分別是C的真子集和真母集,我們看到在上面兩圖中,
由此可見C是「非單調」的。總括而言,上述量詞是「第1論元遞增,第2論元遞減,第3論元非單調」的。
接著考察「<1,12>型量詞」"(more ... than ...)"的「單調性」,這個量詞的真值條件為
根據類似上面的推理,容易推斷上述量詞是「第1論元非單調,第2論元遞增,第3論元遞減」的。
我們可以從以上對"(more ... than ...)"的分析中總結出以下原理:
以下是上述原理的一些應用實例。試考慮量詞
| (at least n fewer ... than ...)(A, B)(C, D) | ⇔ |B ∩ D| − |A ∩ C| ≥ n |
| ⇔ |B ∩ D| ≥ n + |A ∩ C| |
根據上式,論元B和D處於「多」方,而A和C則處於「少」方,因此根據上面第2點,這個量詞是「第1、3論元遞
減,第2、4論元遞增」的。
其次考慮量詞
| (proportionally more ... than ...)(A, B)(C, D) | ⇔ |A ∩ C| / |A| > |B ∩ D| / |B| |
| ⇔ |B| × |A ∩ C| > |A| × |B ∩ D| |
根據上式,論元C和D分別處於「多」方和「少」方,而A和B則跨越「多」、「少」兩方,因此根據上面第2點, 這個量詞是「第1、2論元非單調,第3論元遞增,第4論元遞減」的(註3)。
第二類「結構化量詞」是指包含兩個以上論元的「同異比較詞」,這類量詞只能體現為<1,12>型的 論元結構。根據上述網頁的表7,這類量詞只有四個,所以我們可以逐一考察其「單調性」。首先考慮 "(different ... than ...s)",其真值條件為
由於這個量詞的真值條件跟"no"非常相似,容易看到這個量詞在三個論元上都是「遞減」的。其次考慮 "(whatever ... also ...)",其真值條件為
根據上式,論元B是「遞減」的,這是因為根據「定理1(2)」,若B' ⊆ B,則有A ∩ B' ⊆ A ∩ B,因此
同理也易見論元C是「遞增」的。至於論元A,則是「遞減」的,以下讓我們來證明這一點。設(3)成立並且A' ⊆ A,我們要證明
設x ∈ A' ∩ B,那麼根據「定理1(2)」,我們有x ∈ A ∩ B。根據(3),我們亦有x ∈ A ∩ C。至此我們有x ∈ A'和x ∈ C,即x ∈ A' ∩ C。由於x是任意的元素,我們證明 了(4)。總結以上推理,我們證明了
即A是「遞減」的。總括而言,上述量詞是「第1、2論元遞減,第3論元遞增」的。
看到這裡,有些讀者可能感到奇怪,為何在(3)中同時出現於「⊆」號左、右兩邊的A不是「非單調」的?
事實上,如果把(3)改為下式,那麼我們可以透過類似3.1小節的「溫氏圖」,證明下式中的A是「非單調」的:
這當中究竟有甚麼奧妙?其實,(3)和(5)存在以下關係:若(3)成立,則必有(5),但反之卻不一定成立。換句
話說,我們可以把(3)看成(5)的一種特殊情況。看到了這一點,上述現象便不難理解。由於(5)涵蓋多種不同情
況,並非在每一種情況下A都是「遞減」的,因此A在較狹窄的條件(3)下具有「遞減性」,但在較廣泛的條件
(5)下卻具有「非單調性」,這是不足為奇的;這一點跟二次函數f(x) = x2在較小的「定義域」x
≤ 0內具有「遞減性」,但在較廣泛的「定義域」−∞ ≤ x ≤ ∞內卻具有「非單調
性」是一樣的。
接著考慮"(the same ... as ...)",其真值條件為
由此可見,
根據與上一章介紹的「並列量詞」類似的推理(註4),我們可以推斷上述量詞是「第1論元遞減,第2、3論元非
單調」的。
最後考慮"(different ... than ...w)",其真值條件為
由於上式是(6)的否定,根據上一章對「算子否定」的討論,我們知道上述量詞是「第1論元遞增,第2、3論元 非單調」的。
第三類「結構化量詞」是指由較簡單的量詞通過「否定」、「合取」、「析取」等而得的複合結構,由此可見
,上一章所討論的「算子否定」和「並列量詞」其實都可看做這類量詞的特例。不過,第三類「結構化量詞」
並不限於由「<1,1>型量詞」構成的複合結構,而可以有多種複雜結構。由於這類量詞是派生性的,它們的「單
調性」一般都可以透過其組成部分的「單調性」推導出來,而無須逐一研究,所以這裡只抽選幾個較有代表性
的例子以作說明。
首先考慮以下這個由「<−,1>型量詞」構成的第三類「結構化量詞」:
我們只需考慮論元A的「單調性」。根據2.2小節,"everything"和"nothing"的唯一論元分別是
「遞增」和「遞減」的,因此它們的「析取」(「並列」的一種)應是「非單調」的。根據「算子否定」的特性
,我們知道上述量詞也是「非單調」的。
其次考慮以下這個「<14,1>型量詞」:
根據「定理1(3)」,若A' ⊆ A,則A' ∪ B ∪ C ∪ D ⊆ A ∪ B ∪ C ∪ D,
因此A是「遞減」的,此一推理亦適用於B、C和D。此外,根據"every"的「右遞增性」,易見E是「遞增
」的。總括而言,上述量詞是「第1、2、3、4論元遞減,第5論元遞增」的。
最後考慮以下這個<<1,12>,1>型量詞(在下式中,m、n和p都是自然數):
為方便分析,我們把這個量詞的真值條件改寫為:
運用筆者在3.1小節總結出來的原理以及有關「並列量詞」的原理,容易根據上式推斷上述量詞是「第1、4論元 非單調,第2論元遞增,第3論元遞減」的。
筆者在《廣義量詞系列:迭代量詞》中介紹了「迭代量詞」的概念,並指出 此一概念可用來表達那些以「及物動詞短語」、「雙及物動詞短語」以及其他複合動詞/形容詞/介詞結構作 為謂語中心的語句。因此,如果我們把「單調性」概念推廣至「迭代量詞」,便可發掘和解釋更多類型語句的 推理模式。在以下的討論中,筆者將要使用以下兩條定理(證明從略):
| 定理2: | 設P、Q為函項,則P(x) ⇒ Q(x)當且僅當{x: P(x)} ⊆ {x: Q(x)}。 |
| 定理3: | 設R(x1, ... xn+1)和R'(x1, ... xn+1)為n + 1元函項,則對任何y1, ... yn而言,有 |
| R ⊆ R' ⇒ {xn+1: R(y1, ... yn, xn+1)} ⊆ {xn+1: R'(y1, ... yn, xn+1)}。 |
由於「迭代量詞」是派生性的,即由較簡單的量詞通過「迭代」運算複合而成,這類量詞的「單調性」應能由 其組成部分的「單調性」推導出來,而無須逐一研究。舉例說,讓我們分析以下「迭代<1,1>型量詞」的「單調 性」:
首先考慮論元A,根據上式,容易看到A是「遞減」的。請注意此一結果其實反映了"every"的「左遞減
性」。
其次考慮論元B。設B ⊆ B',那麼容易看到
請注意上述結果其實反映了"some"的「左遞增性」。接著,根據「定理2」,有
由此得
即B是「遞增」的。
最後考慮論元C。設C ⊆ C' (其中C和C'均為二元函項),那麼根據「定理3」,我們有
由此得到
請注意上述結果其實反映了"some"的「右遞增性」。由於上式跟(7)非常相似,因此運用與上面分析B的
「單調性」類似的推理,容易推得C也是「遞增」的。總括而言,上述「迭代量詞」是「第1論元遞減,第2、3
論元遞增」的。換句話說,上述「迭代量詞」的「名詞性論元」A和B的「單調性」剛好分別等同於
"every" 和 "some"的「左單調性」,而「謂詞性論元」C的「單調性」則等同於"some"
的「右單調性」。
接著讓我們看一個更複雜的例子。試考察以下量詞的「單調性」:
首先考慮論元A,容易看到A是「非單調」的。
其次考慮論元B。設B' ⊆ B,那麼我們有
因此根據「定理2」,有
由此得
即B是「遞減」的。
接著考慮論元C。設C ⊆ C',那麼我們有
因此根據「定理2」,有
由此得到
由於上式跟(8)非常相似,因此運用與上面分析B的「單調性」類似的推理,可以推得C是「遞增」的。
最後考慮論元D。設D' ⊆ D (其中D和D'均為三元函項),那麼根據「定理3」,我們有
由此得到
由於上式跟(9)非常相似,因此運用與上面分析C的「單調性」類似的推理,可以推得D是「遞減」的。總括而言
,上述「迭代量詞」是「第1論元非單調,第2、4論元遞減,第3論元遞增」的。換句話說,上述「迭代量詞」
的「名詞性論元」A、B和C的「單調性」剛好分別等同於"most"、"no"和"~every"的「
左單調性」,而「謂詞性論元」D的「單調性」則等同於"~every"的「右單調性」。
從上述兩個例子我們可以總結出以下一般原理。設(Q1 ... Qn)(A1 ...
An)(B)為由n個「<1,1>型量詞」組成的「迭代量詞」,其中A1 ... An為
「名詞性論元」,B為「n元謂詞性論元」:
為方便應用上一小節介紹的一般原理,以下將借助筆者在《廣義量詞系列:時間 量化結構》中介紹的「迭代<1,1>型量詞」的「三分結構」來推導這類量詞的「單調性」。利用這種 「三分結構」,上一小節討論的「(most ... no ... every)(A, B, C)(D)」可以表達為:
現在我們可以沿用筆者在上一章介紹的「單調性推理原理」推斷上面各個論元的「單調性」,與上一章不同的
是,在上式中,某些論元處於多個量詞的「轄域」之內,而且相對於不同量詞,可能處於不同的論元位置。以
論元C為例,它便處於"every"、"no"和"most"的「轄域」之內,而且相對於這三個量詞
,C分別處於左論元、右論元和右論元位置。由此可見,處於愈內層的論元便愈可能受到「遞減性」、「非單調
性」或「否定性」的影響,但只要靈活運用「單調性推理原理」和「多重否定律」,我們總能推斷出「迭代量
詞」各論元的「單調性」,以下筆者舉一個例子以作說明。
以前述的"(most ... no ... every)"為例,首先,由於most ∈ −MON↑,論元
A是「非單調」的。其次,由於no ∈ ↓MON↓,我們可以把"no"看成一種「左、
右論元否定詞」,因此論元B相當於受到一重否定,因而是「遞減」的,而處於更內層的C和D也受到至少一重否
定。最後,由於every ∈ ↓MON↑,我們可以把"every"看成一種「左論元否定詞
」,這樣論元C便總共受到兩重否定,因此C是「遞增」的,而只受到一重否定的D則是「遞減」的。此一結果與
上一小節的分析完全一致。根據上述結果,我們知道以下推理是有效的:
請注意在上述兩句中,儘管動詞「推薦」出現於句中,但它作為「謂詞性論元」卻對應於(10)中的最後一個論
元D。
我們還可以進一步研究各種否定對(10)的影響。由於(10)含有七個部分(四個論元和三個量詞),相應地可以在
七個層面進行否定。我們不一定每次只對一個層面進行否定,而是可以同時對多個層面進行否定。現在假設我
們對量詞"most"和論元B進行否定,使(10)變為
由於量詞"most"位於最外層,對它的否定波及所有論元,而對B的否定則只影響B。不過由於論元A在 "most"影響下呈「非單調性」,它不受任何否定影響。至於論元B、C和D,則分別相當於受到三重、三 重和兩重否定,因此分別呈「遞減性」、「遞減性」和「遞增性」。根據上述結果,我們有以下有效推理:
請注意由於「三分結構」具有清晰簡潔的優點,即使對於一些結構複雜的「迭代量詞」,我們也能容易推導其 「單調性推理」模式。
「三分結構」也可用來分析「迭代<−,1>型量詞」的「單調性」,唯一不同之處是這類量詞沒有「名詞性 論元」,因此只需考慮其「謂詞性論元」的「單調性」。現在讓我們研究以下量詞的「單調性」:
根據前面對「光桿名詞短語」和「第一類泛化量化結構」的處理,這個量詞可以表達為以下「三分結構」:
在上式中,儘管"every"相當於一個「左論元否定詞」,但由於論元A相對於兩個"every"都是處 於右論元位置,所以不受任何否定影響,因而是「遞增」的。以下推理是上述結果的一個實例:
筆者在《廣義量詞系列:時間量化結構》中還介紹了「迭代結構化量詞」的 「三分結構」,其優點是簡潔地顯示了各個論元相對於各個量詞的「轄域」和論元位置,因此也可用來確定這 些論元的「單調性」。舉例說,以下量詞
可以表達為以下「三分結構」:
根據"more"的定義,我們可以把"more"的第一和第二論元分別看成「多」方和「少」方。根據 筆者在3.1小節總結出的規律,由於論元E跨越兩方,它是「非單調」的。由於論元B和D處於「少」方,它們受 到至少一重「遞減性」(即「否定性」)影響。由於論元D又處於"no"的「轄域」之內,它再受多一重否 定,因此B和D分別相當於受到一重和兩重否定,因而分別呈「遞減性」和「遞增性」。至於論元A和C,由於它 們處於「多」方,而且"some"並無任何「遞減性」或「非單調性」,所以它們都是「遞增」的。總括而 言,上述量詞是「第1、3、4論元遞增,第2論元遞減,第5論元非單調」的。以下推理是上述結果的一個實例:
我們還可以把上述推理方法推廣應用於含複雜定語的語句,首先考慮含有「定語分句」的句子,以下僅以一例 說明如何用「三分結構」推斷含「定語分句」的句子的「單調性」。試看以下句子:
上句可以表達為以下「三分結構式」:
上式顯示論元BOY、GIRL和LOVE都處在"every"的左論元位置上,由於"every"相當於一個「左論 元否定詞」,這三個論元都受到至少一重否定。由於"some"並無任何「遞減性」或「非單調性」,所以 處在其「轄域」內的GIRL和LOVE跟BOY一樣只受到一重否定,都呈「遞減性」。MOST-HAPPY則處在 "every"的右論元位置上,不受任何否定影響,所以呈「遞增性」。根據上述結果,我們有以下有效推 理:
其次考慮含有複雜「所有格結構」的句子。根據《廣義量詞系列:特殊單式量詞 》,我們可以把語句
表達為以下「三分結構式」:
從上式容易看到論元MEMBER、CAR和RED都呈「遞減性」,因此我們有以下推理:
由於這類語句包含多個量詞,當不同「單調性」的量詞組合在一起時,可能會令某些論元呈「非單調性」,試 看以下語句:
根據上述網頁,上句可表達為以下「三分結構式」:
從上式容易看到論元BOY和FIERCE都呈「遞增性」,至於DOG,則由於這個論元同時出現於"some"和 "every"的左論元位置,它受相反的「單調性」影響,結果它是「非單調」的。事實上,以下兩個推理 是無效的:
上面第一個推理的無效性是容易看到的,至於第二個推理之所以無效,是因為假如該推理的前件是真的,那麼 必有男孩擁有狗,但這並不蘊涵有男孩擁有黑狗,因而後件中的"some boys' black dogs"可能根本不存在,從 而使後件假。
筆者至今討論的「單調性推理」都只集中於「個體論域」上的量詞,但正如筆者在以往一再強調的,量化是自 然語言中的普遍現象,因此「單調性推理」也應適用於「個體論域」以外的論域。在本節筆者將把「單調性推 理原理」推廣應用於其他論域,從而解釋大量推理現象。不過由於並非筆者以往介紹過的每一種量化結構都有 合適的「母集-子集」概念(例如「程度」便沒有這樣的概念,我們難以定義何謂「xx程度的真子集」),所以以 下的討論只局限於某些論域。
在眾多論域中,「時間論域」與「個體論域」最相似,「個體論域」中的多種量詞在「時間論域」中都有相應 的表現形式,因此上文提到的各種「單調性推理」模式可推廣應用於「時間論域」。舉例說,設集合A為「昨天 」,B 為「John穿著紅色T恤的時間」。那麼~A就是「昨天以外的時間」;而語句「John 在昨天以外的小部分 時間不穿紅色的T恤」則可表達為
現在研究這語句各論元的「單調性」。根據上一章的討論,(a minority of) ∈ −MON↓,因此在上式中,論元A具有非單調性,而B則相當於受到雙重否定,應該呈「遞增性」。由 此我們有以下有效推理:
筆者在《廣義量詞系列:時間量化結構》中曾指出,某些表達時間的語句可 被分析成含有「結構化量詞」或「迭代量詞」的句子,例如以下兩句
便可以分別表達為以下「三分結構式」(在下式中,HAVING-MEAL和PRAYING分別代表「John進餐」和「John祈禱 」的事件組成的集合):
現在讓我們推斷以上兩式中各論元的「單調性」。首先,根據(12),由於Time(PLAY-TV-GAME(j))和 Time(READ-BOOK(j))分屬"more"的「多」方和「少」方,而yesterday(X')則跨越兩方,上述三個論元 分別為「遞增」、「遞減」和「非單調」的。由此我們有以下有效推理:
其次,根據(13),由於HAVING-MEAL和PRAYING分別位於"every"的左論元和右論元位置,這兩個論元分 別為「遞減」和「遞增」的。由此我們有以下有效推理:
筆者在《廣義量詞系列:模態量化結構》中曾指出,「相對模態句」(即各 種「條件句」)與「個體論域」上的量化句存在著對應關係。舉例說,以下五個抽象句式
可分別表達為以下「三分結構式」:
根據"every"、"some"、"only"、"(no except World(p)"和"(all except World(p)"的「單調性」以及「單調性推理原理」,容易知道以下推理是有效的(以下沒有關於"if and only if"和"except when ... otherwise"的推理,因為與這兩個連詞對應的量詞是「左、右非單調」的):
對於「絕對模態句」,我們也能進行「單調性推理」,這是因為這類語句可以表達為「第一類泛化量化結構」 ,例如
由此可知以下推理是有效的:
筆者在上述網頁中還曾指出,「無人稱動詞句」可以表達為一種「模態量化句」。舉例說,語句「(現在)下雨 了」便可以表達為
由於上式中的wACTUAL相當於「可能世界論域」中的專有名詞,根據上面2.1小節的討論,可以推知 以下推理是有效的:
筆者在上述網頁亦指出,借助「命題論域」,我們可以把「p真和q真」以及「p真或q真」分別表達為以下「三 分結構式」:
我們首先研究以上兩式的「左單調性」,根據"every"的「左遞減性」和"some"的「左遞增性 」,我們得到以下有效推理:
上述兩個推理分別正是「命題邏輯」中的「合取消去律」和「析取引入律」。
接著我們還可以研究以上兩式的「右單調性」。根據當前邏輯學和形式語義學的分析,有一類「生成世界的謂
詞」稱為「事實謂詞」(Factitive Predicate),包括"know"、"regret"等。這類謂詞的語義特點是,當它們與
任一命題p連用後,便預設該命題是真的,即對任何命題而言,
從「命題論域」的角度看,這等於說BILL-KNOW、BILL-REGRET、~BILL-KNOW和~BILL-REGRET是TRUE的真子集。 把上述結果應用於「單調性推理」中,我們便有以下有效推理模式:
用日常語言表達,這就是
筆者在上述網頁還曾指出,可以把混合了「合取」/「析取」的複合命題表達為「迭代三分結構」,現在我們 看如何用「單調性推理原理」推導一些有趣的結果。舉例說,命題(p ∧ q) ∨ (r ∧ s)可以表達為
儘管上式像前面介紹過的「迭代三分結構」那樣包含兩層「三分結構」,但各層之間沒有變項聯繫,無法應用 前面的「定理2」和「定理3」,所以各層論元的「單調性」只受該層量詞影響,例如{p, q}和{r, s}的「單調 性」只受"every"影響,不受"some"影響。因此在分析各論元的「單調性」時,只需逐層各自分 析,無須應用「多重否定律」。現在我們考慮上式中內層的兩個集合{p, q}和{r, s},它們的「單調性」受 "every"影響。由於"every"是「左遞減」的,我們可以從這兩個集合中各去掉至少一個元素, 所得結果仍將為真。其次,考慮外層的集合{every({p, q})(TRUE), every({r, s})(TRUE)}, 這個集合的「單調性」受"some"影響。由於"some"是「左遞增」的,我們可以在這個集合中隨 意加入任何元素(例如命題t),所得結果仍將為真。由此,我們可以得到以下有效推理:
上式不是唯一有效的推理結果。事實上,根據以上討論,我們至少還可以有以下推理結果:
請注意上述推理結果完全可以根據以下等式並綜合運用「合取消去律」和「析取引入律」得到:
上述結果再一次顯示,利用「量化結構」的概念,我們可以把「命題邏輯」中的很多結果解釋成某個統一框架 下的特例。
筆者在《廣義量詞系列:相關詞與度量結構》中曾指出,「最高級」和「 比較級」分別與量詞"every"和"some"存在某種對應關係,因此原則上我們也可以對「比較結 構」進行「單調性推理」。試看以下語句及其「三分結構式」:
由於"every"和"some"都具有「右遞增性」,而且
容易得到以下有效推理:
在考察「比較結構」的「左單調性」時,則存在一個問題,這就是「最高級」和「比較級」語句一般帶有預設 ,例如上面的例句便預設了John是語句中所提到的那一「班」(即上式中的集合CLASS)的一分子。以往筆者在討 論這類結構的「直接推理」和「三段論推理」時,只要規定有關語句是有關同一個集合CLASS,通常不會產生問 題。可是,由於「單調性推理」涉及到真母/子集的問題,便可能產生不符合預設的問題。由於
所以「比較級」語句的「左遞增推理」不會引致不符合預設的問題,例如以下推理:
但由於
所以「最高級」語句的「左遞減推理」可能會引致不符合預設的問題,例如以下推理(假設John是男生):
不過,上述推理的問題只是由於「最高級」的預設問題。如果我們改用另一種不帶上述預設的方法表達上面推 理中的後件,上述問題便不再存在,例如:
筆者在上述網頁中還指出了一般「序數詞」與「例外量詞」的對應關係,即「序數詞」"nth"對應著「例外量詞 」"(all except n − 1)"。由於在上一章中,筆者已證明上述形式的「例外量詞」具有「左、右 非單調性」,我們可以推斷以下推理的無效性:
不過,上述論斷不適用於"first"和"last"這兩個極端「序數詞」。由於這兩個「序數詞」分別對應著量詞 "every"和"no",它們具有與這兩個量詞相似的推理模式,例如:
筆者在上述網頁中亦介紹了「不可數名詞」和「部分-整體關係」,並指出可以使用「整體」的概念表達這兩類 結構。舉例說,以下兩句
便可以分別表達為(在下式中,RIVER代表正在談論中的那條河的河水):
接著讓我們分析以上兩句的「單調性」,首先考慮(14)。儘管(14)中的「⊆」是「整體論」下的關係,但 容易驗證此一關係具有與集合論下的「包含」關係相同的性質,因此該句具有與「全稱量化句」相似的推理模 式,例如
其次考慮(15)。有些人可能覺得由於(15)表現為一個等式,該句似乎具有「非單調性」。但回顧上述網頁, (15)原來的形式是
只是由於在上式中,「⊆」左邊的集合是右邊的集合的母集,根據集合論的原理,我們才把上式改寫為 (15)。事實上,不論是根據上式還是根據「全」字的語義,「John全身濕透」都應被理解為一個「全稱量化句」 ,因此應具有以下推理模式:
我們可以用反證法來證明即使根據(15),上述推理仍是有效的。首先把(15)中「=」號兩端的集合分解為兩個互 斥的集合(分別代表John的上、下半身):
並假設(16)的後件不成立,即
那麼基於(15)、(17)-(19),必有
但這是不可能的,由此證明(16)的後件必真,即該推理是有效的。
「單調性推理」在本質上是有關集合的推理,但其原理其實與某些數學原理有相通之處。筆者在3.1小節總結出 的一般原理便對應著以下有關數值比較的事實:
以下是上述原理的一些推理實例:
我們可以把上述原理應用於某些「量化結構」的推理中,這是因為在某些情況下,我們需要直接對「量化結構」 的數值進行推理。舉例說,筆者在《廣義量詞系列:時間量化結構》中曾指 出,表達「絕對時間量」的「三分結構式」Q(A)(B)中的Q和A、B應分別採取數學運算符和數值(可能含有計量單 位)的形式,例如:
由於「John睡覺的時段集合」是「John熟睡的時段集合」的母集,「John贏得頭獎的事件集合」則是「John得 獎的事件集合」的子集,而母集的基數必然不少於子集的基數,我們有以下有效推理:
我們可以綜合運用前述的各種原理,推斷「混合量化結構」的「單調性」,以下僅舉一例以作說明。語句
涉及「可能世界論域」、「個體論域」和「時間論域」,可以表達為以下「三分結構式」(在下式中,TIME(a) 代表「該節目的頒獎環節所佔去的時段」):
現在讓我們分析上式中各論元的「單調性」。由於"every"相當於「左論元否定詞」,而CHAMPION位於 兩個"every"的左論元位置上,這個論元相當於受到雙重否定,因而是「遞增」的。SONG和SING則位於 外層"every"的左論元和內層"every"的右論元位置上,這兩個論元相當於受到一重否定( "(at least 1)"沒有「否定性」),因而是「遞減」的。上式中的
則表達了一個數值比較關係,根據5.6小節的討論,我們可以把這個「不等式」中的「|Time(a)|」和「1 h」分 別換成較大和較小的數字而不影響「不等式」的有效性。基於以上分析,我們有以下有效推理:
在上一節筆者沒有討論「空間論域」,這是因為「空間關係詞項」(包括表達空間關係的介詞以及少數動詞/形
容詞,如"overlapping"等)有其獨特的「單調性」概念。事實上,Zwarts和Winter在Vector Space
Semantics: a Modeltheoretic Analysis of Locative Prepositions一文中為這類詞項定義了兩種「單調
性」,本節將介紹這些概念。
筆者在《廣義量詞系列:空間量化結構》中曾指出,我們可以採取兩種方式
處理「空間關係詞項」。以"above"為例,我們既可以把它處理成以一個點集合為輸入值,並輸出一個向量集合
的一元函項ABOVE,也可以把它處理成以兩個點集合為輸入值,並輸出一個真值的二元函項above,例如
語句「A在B之上」便可以有以下兩種表達法:
以下介紹的兩種「單調性」將分別用到上述兩種表達方式,為清楚區別這兩種方式,以下將沿用上述網頁的辦 法,用大寫正體字母表示「空間關係一元函項」(例如ABOVE),並用小寫斜體字母表示「空間關係二元 函項」(例如above)。
如前所述,我們可以把某些含有「空間關係詞項」的語句表達為「三分結構」Q(A)(B)的形式,其中Q是「空間
關係二元函項」,A和B則是點集合。這樣我們便可以把「<1,1>型量詞」的「單調性」概念推廣應用於「空間關
係二元函項」,從而得到「點單調性」(Point Monotonicity)的概念(註5),其中「左/右遞增/遞
減/非單調」等概念的定義跟「<1,1>型量詞」的相應概念大致相同,這裡不再贅述。惟須注意的是,為區別於
下文要介紹的另一種「單調性」,本文使用「PMON」作為「點單調性」的代號,例如↓PMON↑便代表
具有「左點遞減性、右點遞增性」的「空間關係詞項」組成的集合。
正如筆者在以往指出的,「空間關係詞項」"inside"、"outside"和"overlapping"分別
與量詞"every" 、 "no" 和 "some"存在對應關係,所以這三個「空間關係二元函項」
也分別具有與上述三個量詞相似的「左、右點單調性」,即
以下是上述結果的推理實例:
除了上述三個最基本的「空間關係二元函項」外,其他「空間關係二元函項」大多數是「左、右點非單調」的 。現以"above"為例作出說明,請看下圖:

在上圖中,B' ⊆ B ⊆ B''。我們發現儘管「A在B之上」是真的,但「A在B'之上」卻是假的,這是因
為B'某些以A的點為「終點」的「外部最近向量」(例如圖中的v)與垂直線的夾角大於45°,不符合
筆者在上述網頁介紹的"above"的定義(該定義要求|vup| >
|v⊥up|)。同樣,上圖亦顯示「A在B''之上」也是假的,因為事實上A是在B''之內。
總上所述,"above"是「右點非單調」的,同理亦可以證明"above"也是「左點非單調」的。對
於其他表達空間位置的介詞,也可以用相似的方法證明其「左、右點非單調性」。
表達距離的「空間關係詞項」的情況則有所不同。首先考察"(far away from)",筆者在
《廣義量詞系列:三段論推理的革新》的(15)中實際上證明了
由此可見,"(far away from)"是「右點遞減」的。基於相同原理,也易證"(far away from)" 是「左點遞減」的,即
根據對稱性,"(far away from)"的反義詞"near"似乎應該屬於↑PMON↑。但根據定義 ,「near(A)(B)」成立的必要條件是A與B不重疊。可是,當我們把A或B換成其真母集A'或B'時,無法保 證A與B'不重疊,或A'與B不重疊。由此可見,"near"實際上屬於−PMON−。基於相同理由, 表達極短距離的"on"也屬於−PMON−。
正如上一小節所述,自然語言中大多數「空間關係詞項」都是「左、右點非單調」的,因此儘管「點單調性」 的概念相當直觀,但似乎是一個沒有太大適用性的「單調性」概念。為此,Zwarts和Winter又引入了「向 量單調性」(Vector Monotonicity)的概念。在介紹此一概念前,我們需要「左向量序」(Left Vector Order)和「右向量序」(Right Vector Order)的定義(註7):對任何一對具有相同「起點」的 向量v、v'而言,我們說v ≤l v'當且僅當存在一個實數r ≥ 1使得v' = r • v。對任何一對具有相同「終點」的向量v、v'而言,我們 說v ≤r v'當且僅當存在一個實數r ≥ 1使得v' = r • v。上文定義中「≤」的下標「l」和「r」分別代表「左向量序」和「右向量序」。以下兩圖直觀地 顯示「左向量序」和「右向量序」的概念:

有了上述概念,我們便可以作出如下定義:設P為「空間關係一元函項」,A、B為點集合。我們說P是「左 向量遞增」(Left Vector-Increasing)的當且僅當
P是「左向量遞減」(Left Vector-Decreasing)的當且僅當
P是「右向量遞增」(Right Vector-Increasing)的當且僅當
P是「右向量遞減」(Right Vector-Decreasing)的當且僅當
有關「左/右向量(非)單調」的概念類似「<1,1>型量詞」的相應概念,這裡不予贅述。類似上文,以下使用「
VMON」作為「向量單調性」的代號。
以下以「空間關係一元函項」ABOVE為例闡明上述概念,這個函項是「左、右向量遞增、遞減」的(註8),即
以下四圖可驗證ABOVE滿足(20)-(23)的條件:
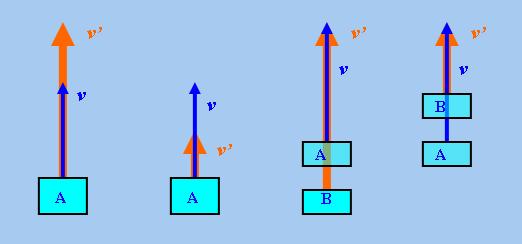
我們可以把上述結果應用於某些日常推理中。舉例說,從上面最左圖,我們可以得到以下「左向量單調性推理」 (以下把A理解為某幢房子的屋頂,並把v和v'分別理解為某架飛機和某隻鳥兒在某一時刻相對於 屋頂的位置向量):
| 前提1: | 鳥兒在屋頂之上。 |
| 前提2: | 鳥兒介於屋頂與飛機之間。 |
| 結論: | 飛機在屋頂之上。 |
請注意基於上面對「向量序」的定義,我們在這裡必須把「X介於Y與Z之間」理解為「X在Y與Z的某條連線的某
一中間點上」,而不能是前述網頁中介紹的較寬鬆的空間關係BETWEEN。比較上面的「前提1」和「結論」,可
以看到上述推理涉及語句「above(A)(B)」中左論元A的變化,故稱為「左向量單調性推理」。
同理,從上面最右圖,我們可以得到以下「右向量單調性推理」(以下把A和B分別理解為山頂和雲層,並把
v和v'分別理解為某架飛機相對於山頂和雲層的位置向量):
| 前提1: | 飛機在山頂之上。 |
| 前提2: | 雲層介於山頂與飛機之間。 |
| 結論: | 飛機在雲層之上。 |
請注意上述推理涉及語句「above(A)(B)」中右論元B的變化,故稱為「右向量單調性推理」。
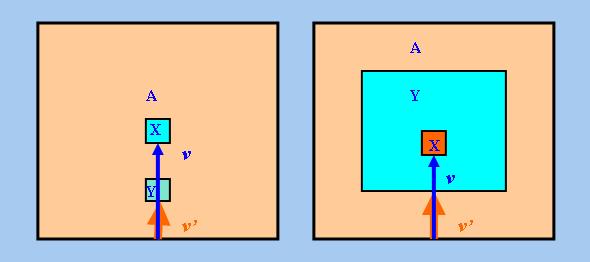
容易看到,大多數表達空間位置的詞項都具有ABOVE那樣的「向量單調性」(註9),不過也有少數例外。INSIDE
便是一個顯著的例子,儘管這個詞項是「左向量遞減」的,但卻不是「左向量遞增」的,這是因為把點集合A的
某一個「內部最近向量」延長後,所得結果不一定仍是A的「內部最近向量」(該向量的「終點」可能不再在A
內)。至於「右向量單調性」,以下兩圖顯示,儘管v'是B的「邊界向量」,但卻不一定是B的「內部最
近向量」:

由此得到
以下是上述結果的推理實例:
| 前提1: | X在A之內。 |
| 前提2: | Y介乎X與A之間。 |
| 結論: | Y在A之內。 |
惟請注意,由於INSIDE在語義上的特殊性,上面「前提2」中的「Y介乎X與A之間」代表著與前面所述很不同的 情況,至少可包括以下兩種情況:
最後討論表達距離的「空間關係詞項」。容易看到,
這是因為當我們把一個本來大於某長度標準s的向量朝箭頭或箭尾方向延長後,所得向量的長度也必大於s;但 在把這個向量縮短後,所得向量的長度卻不一定仍大於s。基於相同原理,與FAR-AWAY-FROM相反的NEAR以及表 達極短距離的ON應具有相反的「向量單調性」,即
「單調性推理」是當代廣義量詞理論提出的新推理模式,但它與古典推理卻有一定的聯繫。Hoeksema在 Monotonicity Phenomena in Natural Language一文中便指出「單調性推理」與古代的「曲全公理」 (Dictum de Omni et Nullo)有相通之處(註10),而「曲全公理」又是「三段論推理」的普遍依據,由此可見「 單調性推理」與「三段論推理」的聯繫。事實上,我們可以把某些「三段論推理」的有效格式重新詮釋為當代 的「單調性推理」。以「AAA-1式」為例,其抽象格式可以表達為
| 大前提: | every(A)(B) |
| 小前提: | every(A')(A) |
| 結論: | every(A')(B) |
請注意我們可以把上述推理模式重寫為
上式正是"every"的「左遞減性」的定義,由此我們可以把傳統「三段論推理」的「AAA-1式」看成 "every"的「左單調性推理」的古典版本,其餘某些「三段論推理」的有效格式也可以作類似的詮釋。 由此可見,我們可以把當代的「單調性推理」看成把某些「三段論推理」有效格式從"every"、 "some"和"no"推廣至更多量詞的嘗試。
到目前為止,筆者所討論的「左/右單調性」的定義都是把「三分結構」Q(A)(B)中的Q固定而讓A/B變化。現
在的問題是,如果我們把A和B固定而讓Q變化,能否得到一種新的「單調性」定義?本小節嘗試探討這個問題。
根據筆者在《廣義量詞系列:直接推理的革新》提出的「對當方陣一般模
式(第二形式)」,給定「單向蘊涵關係」:
便可構造以下「對當方陣」:
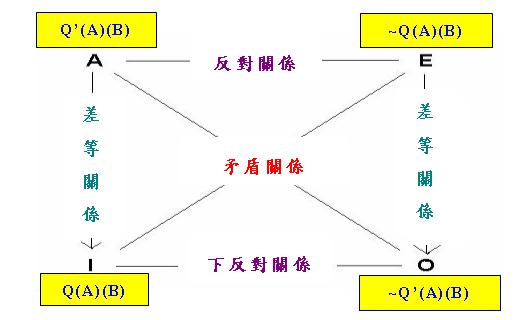
現在讓我們從另一個角度看上圖的「差等關係」。根據集合論,兩類事物之間的關係可理解為由「集合有序對」 組成的集合。由於「<1,1>型量詞」表達兩個集合之間的關係,它們可以被看成「集合有序對」的集合,例如 "every"便可以定義為
這樣,語句「Q(A)(B)」便可以重新表達為 (A, B) ∈ Q,而前述的(24)則可以改寫為
但上式正是「真子集」的定義,即
這樣我們便把量詞重新理解為集合,並把量詞之間的「差等關係」重新理解為集合之間的「真包含關係」。同 樣,量詞之間的「蘊涵關係」也可以重新理解為集合之間的「包含關係」:
舉例說,根據「古典對當方陣」,我們有(假設「主語存在預設」成立):
把量詞看成集合(一種「高階集合」)後,我們便可以定義作用於這些集合的「高階算子」。由於在廣 義量詞理論下,量詞被視為語句(即命題)的核心,作用於量詞的算子就是作用於命題的算子,即「命題聯結詞」 ,因此我們可以把「命題聯結詞」看成「高階算子」。下表列出一些常用「高階算子」的真值條件(在下表中, A、B、C、D為集合)(註11):
| 論元結構 | 真值條件 |
|---|---|
請注意在上表中,"not"被定義為「高階一元算子」,它以一個量詞作為其論元,把
"not"作用於量詞Q後,所得結果"not(Q)"相當於一個「<1,1>型量詞」(它以兩個集合作為其論
元);"if"(以及其餘四個算子)則被定義為「高階二元算子」,它以兩個量詞作為其論元,把
"if"作用於量詞Q和Q'後,所得結果"if(Q)(Q')"相當於一個「<<1,1>,<1,1>>型量詞」(它以四
個集合作為其論元,這四個集合又分成兩組)。
接著讓我們考察「高階一元算子」"not"的「高階單調性」(Higher Order Monotonicity)。
根據上述「對當方陣」以及表1的定義,我們有
把上述結果與筆者以往提出的「遞減性」的定義比照一下,可以看到上述結果其實反映了一種「遞減性」。事 實上,一般地,給定「高階一元算子」O1,我們可以把「遞減性」定義為
利用(25),我們可以進一步把上述定義化簡為
現在容易看到,(26)與(27)具有相同的形式。由此我們得到以下結果(在下式中,HMON代表「高階單調性」):
仿照上面的處理方法,我們可以定義「高階二元算子」的「左、右單調性」如下:設O2為「高階二 元算子」,那麼O2的「左遞減性」可定義為
其他「單調性」概念也可以作出類似定義。舉例說,"if"就是「左遞減」的,以下讓我們來證明這一點 。設Q' ⊆ Q和[if(Q)(Q'')]((A)(B))((C)(D)),那麼根據(25)和表1,我們分別有
根據「假言三段論」,我們有
而根據表1,上式等同於
由此可見,"if"滿足(28)的條件,即"if"是「左遞減」的。類似地,我們也可以證明 "if"是「右遞增」的,即
以下是上述結果的一個推理實例:
基於相同原理,我們也可以證明其他「高階二元算子」的「高階單調性」:
請注意普通的「單調性推理」是同一個量詞下的推理,通過「高階單調性」的概念,我們可以得到不同量詞之 間的推理模式,而這正是「對當關係推理」的特點,由此我們看到了傳統「對當關係推理」與當代「單調性推 理」的聯繫。
註1:其實上述網頁也討論了「<1,1,1>型疑問量詞」,不過由於「<1,1,1>型疑問量詞」在本質上只是在「 <1,1>型陳述量詞」的原有論元結構上加上一個「解答論元」後形成的量詞,所以我們可以把「<1,1,1>型疑問 量詞」看成「<1,1>型陳述量詞」的變體。

