本題是純數學上常見的「存在性問題」(Existential Problem),即探討某一對象(本題為所需的推銷員路線)
是否存在的問題。存在性問題的解答只有兩個,要麼存在要麼不存在,但兩者的證明方式卻有很大差異。一般
而言,要證明某一對象存在,我們有兩種選擇,直接證明和間接證明。直接證明又稱「構造性證明」(
Constructive Proof),即直接構造出所要求的對象或講出構造這對象的方法。例如要證明二次方程x2
+7x+12=0存在實數解,我們只需舉出x=3和x=4這兩個解,並證明它們的確滿足上述二次方程便行了。有
時直接證明法很難進行,我們便惟有借助間接證明法,即採用各種數學方法間接證明所求對象確實存在,但卻
不說出這對象是甚麼。例如在解上述二次方程時,我們也可利用它的「判別式」(Discriminant),即72
- 4 x 1 x 12 = 1 > 0,從而證明該二次方程存在兩個實數解,至於這兩個實數解是甚麼,則不必求
出來。
如要證明某對象不存在,一般只能借助間接證明法(除非該問題所涉及的對象很少,可以逐一考察所有對象)。
請注意,不能因為你已用盡現時所知的所有方法也找不到所求對象便說該對象不存在,因為現時沒有適當的方
法藉以找到所求對象,並不代表永遠都沒有適當的方法。或許將來會發展比現時好得多的方法,從而解決現時
解決不了的問題。因此,要證明某對象不存在,便必須證明此對象的存在是與某種已知的事實相矛盾。由於數
學不容許矛盾存在,這便可間接證明該對象是不可能存在的了。
現在讓我們來看看這度題的解答。相信各位讀者在作出多番嘗試後也找不到所要求的路線;不過你不能就此說
這條路線是不存在的,你必須證明這條路線的存在與某些已知事實相矛盾。如何找出這些矛盾?讓我們跟著
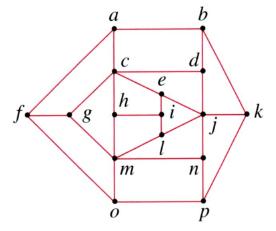
提示做。以下分述(a)部分和(b)部分的解答。為方便讀者參考,以下重複顯示本題的附圖。
(a) 根據提示,我們要刪去圖中的線段,使每一點只與另外兩點相連。先看點d,該點與另外三點相連
,即c、e、g。我們必須刪去其中一條線段。不過由於點c和e本來就只與另外兩點相連,所以在點c和e上的線
段不能動(否則點c或e便會成為只能進不能出的點,構不成一條循環路線),因此我們便只能刪去連接d與g的線
段。同理,點b與點a、c、g相連,也須刪去其中一條線段。但由於點a和c上的線段不能動,所以只能刪去連接
b與g的線段。接著看點g,現在它與點f、h、i、j相連,所以必須刪去其中兩條線段。可是在f、h、i、j這四
點上本來就只有兩條線,沒有一條線可以動。於是我們陷入了一個矛盾,在點g上的線必須刪去其中兩條,但
沒有一條可以刪。此一矛盾間接證明了我們不可能找到所需的路線。

請注意在上述推理過程中,我們不是隨意選擇要刪除的線段,而是選擇那些「非刪不可」的線段。因為只有這
樣才使得以上導出的矛盾具有「無可避免性」,從而證明所需的推銷路線不可能存在。
(b) 本題的答案跟上題一樣,但由於本題的圖較上題複雜得多,不宜採取上題那種選擇「非刪不可」線段的方
法。不過本題所用的原理仍是跟上題一樣。概言之,本題是從兩個不同角度計算圖中「非刪不可」線段的數目
,指出從這兩個角度所得的計算結果互相矛盾。首先,我們注意到這幅圖共有16個點和27條線段。由於所求的
路線須經過每一點剛好一次(起點和終點除外),因此所求的推銷員路線須有16條線段。這即是說我們必須在原
圖中刪去27 - 16 = 11條線段,不多也不少。這是從第一個角度計算「非刪不可」線段的數目。接著讓我們考
察圖中的點。請注意這幅圖雖然看似複雜,但其結構其實很有規律。在16個點中,有3個點(c、j、m)有5條線
段,其餘13個點均各有3條線段。首先考慮c、j、m這三點。由於在這3點上各有5條線段,我們必須從每點刪去
其中3條線段,即總共刪去3 x 3 = 9條線段。請注意這9條線段是「非刪不可」的,至於是哪9條線段,我們可
以不管。接著考慮不與c、j、m任何一點連接的點,這樣的點共有4個,即b、f、i、p。由於在這4點上各有3條
線段,我們必須從每點刪去其中1條線段。另外,又由於這4點不與c、j、m任何一點連接,因此從這4點刪去的
線段必定不屬前述「非刪不可」的那9條線段。總括而言,我們必須從這圖中刪去至少9 + 4 = 13條線段(這裡
說「至少」13條線段是因為圖中還有7個點我們尚未考慮,我們可能還要刪去這些點上的某些線段),可是這樣
卻跟前面從「第一個角度」計算的結果相矛盾,此一矛盾間接證明了我們不可能找到所需的路線
。