猜謎題，學推理


本網頁收集筆者所曾看過值得向大家推介的謎題，這些謎題的共同點是可以啟發你的邏輯思維。每道題都附有 作者的解答，詳細解釋答案。此外，每題均標明「學習重點」，點出你可以從該道題學習到的東西。 惟請注意，筆者提供的解答不一定是唯一的解題方法，也未必是最簡潔的解答，歡迎讀者提供其他謎題和更佳 的解答。

(1) 特難算術題

學習重點：「特殊化」的解題技巧

試求1 + 1 x 2 + 1 x 2 x 3 + 1 x 2 x 3 x 4 + ...... + 1 x 2 x 3 x 4 x ...... x 1958這個數的個位數 。

解答(1)



(2) 握握手，做個好朋友

學習重點：抽絲剝繭式的推理

陳先生和太太出席晚宴，和另外三對夫婦會面。他們見面後互相握手。假設他們不會跟自己握手，也不會跟自 己的配偶握手，而且不會跟同一個人握手多於一次。在大家握完手後，陳先生詢問每一個人(包括他的太太， 共7個人)的握手次數，7個人的答案都是不同的。

(a)請問陳先生握了多少次手？
(b)陳太太又握了多少次手？

解答(2)



(3) 戴帽子

學習重點：反證法

有6頂帽子，其中三頂是紅色，兩頂是黃色，一頂是藍色。現把其中4頂戴在4個人的頭上。這4個人站在一條直 線上(不妨把他們稱為「1號」、「2號」、「3號」和「4號」，數字較小的站在前)，站在較後的可以看到較前 位置的人的帽子，但不能看見較後位置的人的帽子，也不能看見自己戴的那頂帽子。假設這4個人都有推理能 力，不會瞎猜，而且能夠聽見我跟他們每個人的對話。現在我問4號是否知道他戴的帽子的顏色，他望望站在 前面的3個人的帽子，想了想後答曰：「不知道」。接著我問3號同樣的問題，他也望了望前面兩個人的帽子， 分析一下剛才4號的答案，然後答曰：「不知道」。同樣我又問2號，他也是答「不知道」。最後當我問1號時 ，他便答：「知道」。請看附圖。




(a) 請問1號戴的帽子是甚麼顏色？
(b) 假如4個人都答「知道」，那麼他們戴的帽子分別是甚麼顏色？

解答(3)



(4) 推銷路線

學習重點：「存在性問題」的證明技巧、圖論的知識

(a) 假設下圖的點(a - j)代表某市鎮10間店鋪的位置，各線段代表連接這些店鋪的道路。某推銷員想設計某 條推銷路線，這條路線須為一條循環路線，即終點須與起點相同，且須經過每間店鋪剛好一次，不多也不少( 起點和終點除外)，但不得重複走任何道路。請問你能否替他找到這條路線？如能，請畫出這條路線。如不能 ，請解釋為何不能。




(b)假如換了以下的市鎮店鋪位置圖，答案又如何？




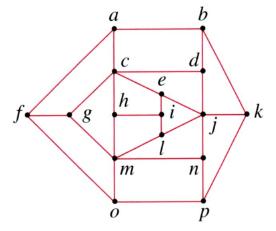
提示：本題是數學上有名的「推銷員問題」(Travelling Salesperson Problem)，所求的路線 稱為「漢密爾頓回路」(Hamiltonian Cycle)。讀者在解答本題時，可以採取以下思路：首先我們須注意到， 如果原圖共有n個點，那麼所要求的路線便須剛好有n條線段(請讀者想想為何是這樣)，因此我們可以把求推銷 員路線視為刪除線段的過程。由於所求路線須經過每一點剛好一次，因此每一點均只能與另外兩點相連，如某 點與超過兩點相連，便須刪去其中某些線。例如在(a)圖中d點與三個點相連(c、e、g)，因此必須刪去其中一 條線。總括而言，解答本題的策略是，把圖中某些線段刪去，使圖中每點均只與另外兩點相連，那麼所剩下的 線段便是所要求的路線。如在刪線過程中出現矛盾，則表示不可能找到所求的路線。

解答(4)



(5) 木星人和火星人排隊

學習重點：排列和組合問題的破解技巧

(a) 現有5名木星人和3名火星人排在一條直線上。假設每位木星人和每位火星人是一模一樣的，換句 話說，可以用5個字母J來代表木星人和3個字母M來代表火星人。如果不許任何兩名火星人站在一起，(舉例說 ，MJJMJMJJ是「合格」的排法，而JMMJJJMJ則是「不合格」的排法)，問總共有多少種「合格」的排法？

(b) 假如5位木星人和3位火星人是各不相同的，換句話說，應用J1、J2、J 3、J4、J5和M1、M2、M3來分別代 表5名木星人和3名火星人，那麼又有多少種「合格」的排法？

提示：鑑於解答本題須應用有關排列(Permutation)和組合(Combination)的知識，這裡有必要 簡介這方面的基礎知識。

典型的「排列」問題是從n個物件中任意抽r個出來排列，並求有多少種排列方法，數學上把此數值記為P(n,r) 。請注意求排列時，是要考慮物件的次序的，因此AB跟BA是不同的，應分別計算。例如從4個物件A、B 、C、D中任意抽2個出來排列，共有12種排法，即P(4,2)=12。這12種排法是AB、AC、AD、BA、BC、BD、CA、CB 、CD、DA、DB、DC。P(n,r)的公式是n!/(n-r)!。這裡n!是n的「階乘」(Factorial)，n! = n(n-1)(n-2)..... 3x2x1。例如4! = 4x3x2x1 = 24。(但如n=0，則定義為0!=1)套用此公式求P(4,2)得4!/(4-2)! = 4!/2! = ( 4x3x2x1)/(2x1) = 12。

典型的「組合」 問題則是從n個物件中任意抽r個出來，並求有多少種抽法，數學上把此數值記為C(n,r)。 請注意求組合時，無需考慮物件的次序，因此AB和BA沒有分別，不應重覆計算。例如從4個物件A、B、C、 D中任意抽2個出來，共有6種抽法，即C(4,2)=6。這6種抽法是AB、AC、AD、BC、BD、CD。C(n,r)的公式是n!/( r!(n-r)!)。套用此公式求C(4,2)得4!/(2!(4-2)!) = 4!/(2!2!) = (4x3x2x1)/(2x1x2x1) = 6。

解答(5)



(6) 海盜分鑽石

學習重點：「逆向思維」方法

現有5名海盜和100顆鑽石，他們協議了以下的方法來分配這些鑽石。

他們首先抽籤決定各人的編號(1至5號)。接著由他們輪流提出分配鑽石的方案，首先由1號提出方案，然後交 大家表決(1號自己也可投票)。他的方案必須取得半數或半數以上(即3名)海盜的贊成方可獲通過，否則他會被 投入海中餵鯊魚。假如1號死掉，則順次由2號提出方案並由大家表決。同樣他的方案也必須取得餘下4人中半數 或半數以上(即2名)海盜的贊成方可獲通過，否則他也會被投入海中餵鯊魚。如此類推。

假設5名海盜都有很高的智慧，在衡量過得失後才作決定。他們均以保存性命為第一條件，同時亦盡量爭取對 自己最有利的結果。此外，本題亦假設這5名海盜都是非常重實利的，即假如他們當中任何一人有兩個方案可供 選擇，而其中一個方案可令他獲得較多利益，他必定會選擇這一方案；但假如該兩個方案能令他獲得相同利益 ，那麼便不能保證他必定選擇任何一個方案。現在問這五名海盜最終會如何分配那些鑽石？有沒有人會死？

解答(6)



(7) 三個質數

學習重點：數論和極值問題求解方法

試求三個質數A、B、C使得A + B + C = 100並且A x B x C的值最大。

規則：不可採用「窮竭法」(即找出A、B、C所有可能的值然後相乘，求其最大值)解答這題。

解答(7)



(8) 天文數字

學習重點：質因數分解法和「floor函數」的應用

試求1 x 2 x 3 x ... 100(在數學上，這樣的算式稱為「階乘」Factorial，可簡記為100!)這個數的末尾有多 少個連續的零。

接著試求1013!這個數的末尾有多少個連續的零。

解答(8)



(9) 五名屋主

學習重點：圖表解題技巧、選言推理方法

有五間房子排成一列，所有房屋的顏色都不一樣，五個屋主來自不同國家，各自飼養不同的寵物、喝不同的飲 料和抽不同的煙，並假設以下條件成立：

  1. 英國人住在紅色的房子裡。
  2. 瑞典人養狗。
  3. 丹麥人喝茶。
  4. 綠色的房子在白色的房子的左邊。
  5. 綠色房子的屋主喝咖啡。
  6. 抽Pall Mall香煙的屋主養鳥。
  7. 黃色房子的屋主抽Dunhill香煙。
  8. 位於最中間的房子的屋主喝牛奶。
  9. 挪威人住在最左邊的房子。
  10. 抽Blend的人住在養貓人家的隔壁。
  11. 養馬的屋主的隔壁是抽Dunhill的。
  12. 抽Blue Master的屋主喝啤酒。
  13. 德國人抽Prince。
  14. 挪威人住在藍色房子隔壁。
  15. 只喝水的人家住在抽Blend的人的隔壁。

現在問，誰養魚呢？

解答(9)



(10) 地下情

學習重點：命題之間的相同、反對和矛盾關係

M小姐氣質高雅，是辦公室中9個男性(A、B、C、D、E、F、G、H、I)心目中共同的偶像，而且在這9人之中，有 一個人正偷偷地和M約會著。下面分別是這9個男人的談話，事後得知只有4個人說的話是真的。那麼，從下面的 對話中，你能推斷出誰是M的情人嗎？

提示：請注意命題之間「反對關係」和「矛盾關係」這兩者的分別。兩個命題是「反對」命題， 如果它們不能同真(但卻可能同假)。例如，上述H和I的說話便是反對命題，它們不能同真，但卻可能同假。兩 個命題是「矛盾」命題，如果它們的關係是如果其中一個真，則另一個必假。例如「J是M的情人」和「J不是M 的情人」便是一對矛盾命題，只要證明了其中一個命題真，則可知另一個命題假。反之亦然，即只要證明了其 中一個命題假，則可知另一個命題真。

解答(10)



(11) 真假難分

學習重點：在推理中靈活運用「正負得負，負負得正」的原理

(a) 在你前往「生命之國」的最後一段旅途中，你來到了一個分岔口。你知道這分岔口上的兩條路其中一條是 通向「生命之國」，而另一條則是通向「死亡之國」。在分岔口上站著兩個人，其中一個人專講真話，另一個 專講假話。你不知道哪條路是「生命之路」，也不知道那兩人中的哪一個專講真話；但那兩人知道哪條路是「 生命之路」，也互相知道對方的特性。現在你可以向其中一人問一條問題，你應如何發問，從而找出「生命之 路」？

(b) 在一個島上住著三個人，一個永遠說真話(姑稱之為T)，一個永遠說假話(姑稱之為F)，一個則有時說真話 ，有時說假話(他說真話或假話的可能性完全是隨機Random的，姑稱之為R)。這三個人互相知道對方的特性，但 只有R才知道自己接下來會說真話還是假話。現在你可以問三條是非問題(即以「是」或「否」回答的問題)，每 條問題均只准向其中一人發問。這三人都懂得你的語言，但他們只會用"da"或"ga"回答你。這兩個詞其中一個 代表「是」，另一個代表「否」，但你不知哪一個是「是」，哪一個是「否」。如果你問了一個他們不知道答 案的問題，他們就會不回答。你應如何發問，從而確定這三個人的身份呢？

注意：

  1. 這三個人智力正常，具有一般人的常識。他們會盡其所知回答你的問題。
  2. F和R在說假話時會「誠實」地說假話，即剛好與其知識相反的答案。
  3. 你可以「隨機應變」地發問，即你所問的問題以及發問的對象可視乎被問者的答案而變化。


解答(11)



(12) 死亡命令

學習重點：當且僅當命題

在一個神秘國度中住著兩類人，一類人有兩隻眼，另一類人有三隻眼。他們沒有鏡子或其他方法知道自己屬於 哪一類人，也不知道這兩類人的總人數，但他們知道確實存在這兩類人。他們全部人每天早上都必定會到市集 聚會。他們全部視力正常，能看到其他人有多少隻眼，而且每天都會見到所有其他人，但卻從不會以任何方式 告訴對方他的身份(這是國家的法律啊)。有一天下午國王發了一道命令，要所有三眼人自殺。國王的命令當晚 便傳達至所有人民。

命令下達後第二天早上，他們如常來到市集，發覺沒有人自殺。第三天早上也發現沒有人自殺。如是者到了第 九天早上，兩眼人發現所有三眼人消失了(他們全部自殺了)。請問這個國家共有多少個三眼人呢？

注意：所有人都是有高度推理能力和絕對服從國王命令的人，每天去完市集回家後便會根據當 天所見作出判斷。如果肯定自己是三眼人的話，便會於當晚自殺。

解答(12)

返回周家發的數學網頁