
ЗАКОНИ ЗА ОТРАЖЕНИЕТО И ПРЕЧУПВАНЕТО,
ОТРАЗЯВАЩА СПОСОБНОСТ НА ПОВЪРХНОСТ
Закони за отражението и пречупването - закон на Снел (Снелиус);
Пълно вътрешно отражение;
Обяснение на отражението и пречупването според принципа на Хюйгенс-Френел. Оптична плътност на веществата.
Отразяваща способност на повърхност,
отражение от диелектрици и метали
Подобно на пропускливостта на веществата t, се определя и отразяващата способност r на дадена повърност.

Ако монохроматичен (едноцветен) светлинен сноп, с дължина на вълната l (представен с лъча L) и с начална интензивност I0, попада върху повърхност под ъгъл a спрямо вертикалата (нормалата) към нея, то интензитетът I на отразената светлина (лъчът L') под ъгъл a' = a, ще бъде поне малко по-слаб, поради поглъщане от материала. Отношението r = I/I0 изразява отразяващата способност на повърхността към съответната дължина на вълната. Най-често отразяващата способност се упоменава в проценти: r% = I/I0*100.
Както и при пропускливостта, за много материали отразяващата способност е различна за различните дължини на вълната. Примерно червена повърхност ще отразява слабо или ще поглъща изцяло синята светлина, както би сторил това червен светофилтър. Среброто, традиционно използвано за нанасяне на огледални покрития, отразява едва 4% от ултравиолетовата светлина с l = 325 nm.
Отразяващата способност зависи и от ъгъла на падане на светлината a (това особено добре личи при диелектриците). Най-слабо отражение имаме при отвесно или почти отвесно падаща светлина - при a от 0 до 30°. С нарастване на ъгъла, отразяващата способност бързо расте и достига 1 при a = 90°. Затова коефициентът на отражение r на дадена повърхност се определя при ъгъл 0° или в границите от 0 до 30°.
Отразяващата способност зависи и от електропроводимостта на отразяващия материал. Колкото с по-висока електропроводимост е той, толкова по-добре отразява. Диелектриците отразяват най-слабо. Например непокрита стъклена повърхност отразява около 4% от светлината. С по-добра отразяваща способност са полупроводниците, а с най-добра - металите. Например качествено полирано просребрено огледало отразява до 98% от светлината. Алуминизирано огледало - до 96%. Метали и сплави като златото, бронза и месинга отразяват най-силно жълтите лъчи и значително по-слабо останалите. Медта - най-силно червените и т.н.
Съществува връзка между показателя на пречупване n на веществото и отразяващата способност на повърхностите на телата, изработени от него. Диелектриците с по-нисък показател на пречупване, отразяват по-слабо.
Някои диелектрични повърхности обаче, покрити с тънки слоеве (до над 10 на брой) от диелектрични материали с голяма разлика в показателите си на пречупване, могат да имат необичайно висока отразяваща способност! Такива са огледалата с нанесени няколко слоя от ZnS и MgF2, с показатели на пречупване съответно 2.3 и 1.43. Такава повърхност има почти 100% отразяваща способност в диапазона от 470 до 650 nm. Висока отразяваща способност и голяма твърдост имат огледалата от няколко слоя ZrO2 и SiO2, с показатели съответно 2.05 и 1.48 - близо 99%, в диапазона от 530 до 570 nm.
Често срещан е обратният случай - чрез нанасяне на тънки (около l/4) диелектрични слоеве върху повърхностите на прозрачни оптични детайли - лещи, призми и др., се постига намаляване на интензитета на отразената от тях светлина чрез интерференчно погасяване на вълните, до около 1 - 2%, а понякога почти до 0! Това са т. нар. антирефлексни покрития или просветляване на оптиката.
Отразената от диелектрична повърхност светлина е отчасти или в голяма степен поляризирана.
Закони за отражението и пречупването
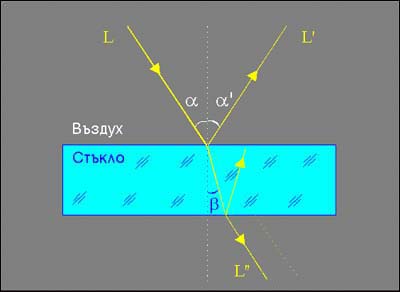
Отражение и пречупване в пластинка от диелектрик (стъкло)
Лъчът L, разпространяващ се във въздушна среда със скорост c1, попада върху повърхността диелектрична (стъклена) плоско-паралелна пластинка, под ъгъл a. Част от светлината навлиза в пластинката, като се пречупва на ъгъл b и продължава с по-ниска скорост c2 през нея, а друга част се отразява от повърхността на ъгъл a'. Падащият, пречупеният и отразения лъч лежат в една равнина, перпендикулярна на повърхността (първи закон за отражението и пречупването), Тази равнина съдържа и перпендикуляра (нормалата) към повърхността, представен в схемата с пунктир, спрямо който са отчетени всички ъгли.
Ъгълът на отражение a' е равен на ъгъла на падане a (втори закон за отражението).
След като премине през пластинката, пречупилия се лъч отново излиза във въздушна среда (при което част от светлината се отразява вътрешно на границата стъкло-въздух), като възстановява първоначалното си направление - L", т.е. L" е успореден на продължението от падащия лъч L (представено с лек пунктир).
Ъглите на падане и пречупване a и b са свързани в следната зависимост (закон на Снел, открит през 1625 г., наречен в чест на Уйлеброрд Снел, 1591-1626):

n21 = n2/n1 = n2/1 = n2
т.е. остава съществен само показателят на пречупване на стъклото n2, който за удобство по-нататък ще бележим само с n.
Пълно вътрешно отражение
Ако светлинен лъч, разпространяващ се в прозрачен диелектрик, достигне границата между него и друга оптична среда с по-нисък показател на пречупване (например стъкло-въздух) под ъгъл a и ако този ъгъл е по-голям от определен граничен ъгъл aгран., се наблюдава пълно вътрешно отражение. Тогава интензивността I на отразената светлина е почти равна на интензивността I0 на светлината, достигаща граничната повърхност, т.е. след отражението, тя изцяло се връща в същата среда, в която се е разпространявала преди. Стойността aгран. на граничният ъгъл зависи от показателите на пречупване на двете среди (от техните оптични плътности).
Да разгледаме случая по-подробно:
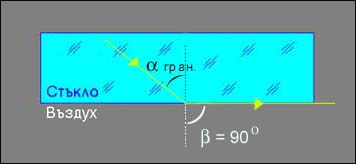
Пречупване при граничен ъгъл на попадащия лъч.
Нека първо светлинния лъч, разпространяващ се в стъклото, достига под ъгъл aгран. границата с въздуха. От двете среди стъклото е с по-висок показател на пречупване (с по-висока оптична плътност). Ъгълът b, на който ще се пречупи лъчът в този случай ще бъде 90°, т.е. пречупеният лъч ще се "плъзга" по повърхността стъкло-въздух (вижте схемата). Тъй като показателят на пречупване на въздуха nвъздух е около 1, според закона на Снел ще имаме:
sin aгран./sin b = sin aгран./sin 90° = sin aгран. = 1/nстъкло
или
nстъкло = 1/sin aгран.
т.е. получаваме абсолютният показател на пречупване nстъкло на средата с по-висока оптична плътност. При различните марки стъкла, граничният ъгъл aгран. спрямо въздуха е около 41° 50'. За водата спрямо въздуха той е 48° 30'.
За пръв път тези ъгли били експериментално установени и описани от Клавдий Птолемей (II в. от н.е.) в неговия труд "Оптика".
Ако повишим ъгъла на падане a, т.е. при a > aгран., светлината ще се отразява изцяло от граничната повърхност в същата оптична среда - ще имаме пълно вътрешно отражение.
Принципа на пълното вътрешно отражение се използва широко в оптиката. Например призмите, изправящи обърнатия образ в биноклите са с пълно вътрешно отражение. Рефрактометърът на Абе, с който се определят показателите на пречупване на захарни разтвори и на различни други вещества, работи на същия принцип. Светловодите (светлинните влакна и кабели) провеждат светлината на дълги разстояния чрез многократни отражения в многослойните си вътрешни повърхности.

Вътрешно отражение на светлина в призма
Обяснение на отражението и пречупването според принципа на Хюйгенс-Френел
Оптична плътност на веществата
По-горе описвахме пречупването и отражението на светлината чрез хода на лъчите, т.е. имахме предвид само геометричните посоки и ъгли. Светлината обаче е електромагнитна вълна и разпространявайки се в дадена среда, тя взаимодейства с нея според принципа на Хюйгенс-Френел.

Успореден светлинен сноп с диаметър d попада върху плоска стъклена повърхност под ъгъл a спрямо нормалата. Разглеждаме една от плоските му светлинни вълни, движеща се със скорост c1 във въздушната среда, единият край на фронта на която в момента t1 достига стъклената повърхност в точка A1. Изобщо в момента t1 положението на нейния фронта е A1B1 (пример a от схемата).
В един следващ момент t2, до повърхността достига и другият край на фронта (в точка B2 - пример b) след като е изминал разстоянието l за интервал време dt = t2-t1 = l/c1. Според принципа на Хюйгенс обаче, точката A1 от стъклената повърхност, в която в момента t1 бе попаднал първият край на фронта, е станала източник (център) на елементарни сферични вълни - една разпространяваща се със същата скорост c1 във въздушната среда и втора, разпространяваща се с по-малка скорост c2 в оптично по-плътното стъкло.
В момента t2, първата елементарна сферична вълна вече има радиус r', докато тази в стъклото - по-малък радиус r". В същия момент t2, допирателната (тангентата) към първата сферична вълна, свързваща точка А2' от нея с точка B2, формира плосък фронт на вълна от отразената светлина, разпространяваща се според втория закон за отражението под ъгъл a' = a спрямо нормалата (разгледайте еднаквите триъгълници A1A2' B2 и A1B1B2, в които ъгъл a' = a). Пак в същия този момент, допирателната към сферичната вълна, разпространяваща се в стъклото, която съединява точка А2" от нея с точка B2, формира плосък фронт на вълна от пречупената светлина, разпространяваща се под ъгъл b спрямо нормалата, съгласно закона на Снел.
Вижда се, че отражението и пречупването на светлината под съответните ъгли се дължи на неедновременното взаимодействие на фронта на падащата вълна със стъклената повърхност, поради ъгълът на падане a и (при пречупването) поради различните скорости c1 и c2 на разпространение на светлината в двете среди. Тези скорости на свой ред се определят от оптичните плътности на средите, които пък зависят от плътностите r на веществата (в kg/m3). Затова по-тежките породи стъкла имат по-високи оптични плътности (те са с по-високи показатели на пречупване).
В момента t2, радиусът r' на елементарната сферична вълна, разпространяваща се във въздуха ще бъде A1B2*sin a' = dt*c1. Аналогично, в същия момент радиусът r" на сферичната вълна в стъклото ще бъде A1B2*sin b = dt*c2. Синусите на двата ъгъла се отнасят помежду си както скоростите на светлината в двете среди:
sin a/sin b = c1/c2
Поради по-малката скорост на разпространение на светлината в оптично по-плътната среда, дължината l на светлинната вълна леко се скъсява.
Вижте също:
Показатели на пречупване на различни марки оптични стъкла и на някои прозрачни вещества;
Коефициенти на поглъщане, пропускливост и екстинкция на вещество;
Поляризация на светлината и въртене на равнината на поляризацията;