Integer
Exponents
![]() Rules for Working with Exponents
Rules for Working with Exponents
Negative Exponents
![]()
Negative exponents are defined as reciprocals.
So
![]()
![]()
The point of the above example is that the exponent rules apply
no matter what the exponents are. Whether the exponents are simple numbers
or complicated expressions with symbols and variables in them, the exponent
rules
apply, they are true.
When you multiply powers to the same base, you add the exponents.
Period. No exceptions!
The Divide Rule
![]()
When you divide powers to the same base, you subtract the exponents.
You always do the exponent on the top minus the exponent on the bottom.
Always!
![]()
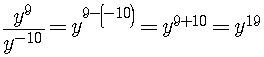
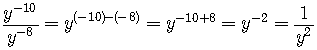
![]()
When you divide powers to the same base, you subtract the exponents.
How big the exponents are is not important, you always do the exponent
on the top (the numerator of the fraction) minus the exponent on the bottom
(the denominator of the fraction).
Again, Look at the examples above, that is what you always do in each example.
The Power Rule
![]()
When you raise a power ![]() to a power m you multiply the exponents,
to a power m you multiply the exponents,
so you get ![]() for
the answer.
for
the answer.
![]()
![]()
![]()
![]()
The Product Raised to a Power Rule
![]()
When you raise a product to a power, you raise each factor
of the product to that power.
![]()
Everything thing that is multiplied is a factor, including the number ![]()
which is multiplying ![]() , so
, so ![]() must also
be raised to the 2nd
must also
be raised to the 2nd
power just like the other factors in the product.
To finish the problem, use the Power Rule,
![]() .
.
Write the final answer using positive exponents only, so
![]() .
.
Here's another example
![]()
Remember that
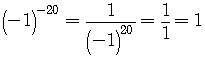 .
.
So
![]()
is the final answer.
The Fraction Raised to a Power Rule
![]()
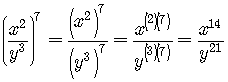
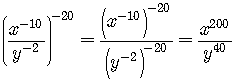 .
.
See Examples 1 - 4, pages 43 - 47.
In particular, look at Example 4, where a complex fraction
is written with negative exponents.
top
next Rational
Exponents