Absolute Value in Equations and Inequalities

The absolute value of a quantity is always greater than or equal to zero.
The absolute value is never negative.

Definition
                     
                                   
Note that if    is negative,   is positive.

Geometrically, we can think of the absolute value of a quantity
as the positive distance from the origin of the quantity.

         = the distance of from the origin =

     = the distance of from the origin =

See Examples 1 - 2, pages 109 - 110.


Equations
Variable appears only on one side of the equation
Solve
            .

Geometrically, we are interested in all the points that are exactly three units
away from the origin of the real number line.
Because the quantity inside the absolute value sign can be positive or negative,
the equation is equivalent to two equations without the absolute value sign,

       
or
       .

Solving each equation, we get the solutions

      
or
     .
In set-builder notation, the solution set is
                         .

Variable appears on both sides of the equation
Solve
                .

The expression inside the absolute sign may be positive or negative
We must look at two cases:

Case 1)      .

For this case,
                             is the range of acceptable values,
and
               ,
so the equation becomes
              

whose solution is
                     
which lies in the range of values acceptable for .


Case 2)     .

For this case,
                          is the range of acceptable values,
and
            ,

so the equation becomes
         
whose solution is
                    
which lies in the range of values acceptable for .

The solution set consists of two numbers

              .


Inequalities
Case 1)     The inequality sign is "less than",   .
Solve
                 .

Geometrically, we are interested in all the points that are within 1 unit of the origin
or exactly one unit away from the origin.
We must rewrite the inequality so that it does not have the absolute value sign, 

      .
These is an inequality with three sides.

     

                  

                 

                  

The solution set is
                                .

The graph of the solution set consists of all the points between the endpoints
and  , including the endpoints.
The solution set is one solid piece.


Case 2)     The inequality is "greater than",    .
Solve
                 .
Geometrically, we are interested in all the points that are farther away
than two units from the origin.
We must rewrite the inequality so that it does not have the absolute value sign.

       
or
        .

These are two independent inequalities, each of which we solve separately.
The first inequality is
       .
The goal is to isolate .
       
or
         

                dividing by a negative number
                                       changes the direction of the inequality

                  .

The second inequality is
         .
The goal is to isolate .

       

          

             dividing by a negative number
                                    changes the direction of the inequality

             

The solution set consists of the numbers less than or the lass greater than ,
                         .


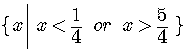Note that this set consists of two disjoint chunks,
the chunk of numbers    or the chunk of numbers  .

The solution set is made up of two separate pieces.

See Examples 3 - 6, pages 111 - 116.


                       top
                       next     Complex Numbers