Complex Numbers

Definition of the Imaginary Unit
                           
                           
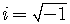
Complex numbers are entities of the form ,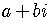
where 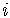is the imaginary unit.
This is the standard form in which the final answer of any calculation
involving complex numbers must be written.

See Examples 1 - 7, pages 121 - 128.

Square roots of negative numbers must be written in terms of  .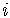
If 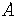is positive, then
            .

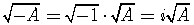See Example 7, pages 127 - 128.


The Arithmetic of Complex Numbers
Addition, subtraction, multiplication, division of complex numbers
obey the usual rules of algebra. Final answers must be written in the form
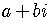. Powers of 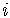   must be simplified.

Powers of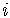
Using the exponent rules,
                
                
                

If the exponent is a negative integer,
                  

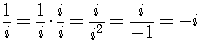
For any integer power of ,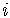
                 .

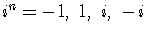Fractions of complex numbers must be rewritten in the standard form  .
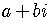The process involves multiplying the top and bottom of the fraction
by the complex conjugate of the bottom.
The conjugate of 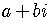   is 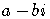   and vise versa.

This works because
     
                                  

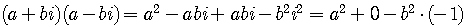
The result of the multiplication does not involve 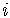, it is a real number.

For example,

     

                   


The final answer is written in standard form.

See Examples 2 - 7, pages 122 - 128.


                       top
                       next     Quadratic Equations