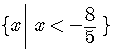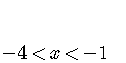Linear Inequalities

Inequality relations, interval notation, union and intersection,
see pages 99 - 103, and examples 1 - 2, pages 100 - 104.

Solving Linear Inequalities
is just like solving linear equations.
To get the solution set for the indicated variable we add, subtract, multiply,
and divide all sides of the inequality until we get the indicated variable alone
on one side of the inequalities.

Some differences:
A) Finite vs. Infinite Set
Let us compare the solution set of the equation  
and solution set of the inequality                        .
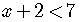The solution set of the equation is the finite set
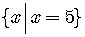       consisting of a single point.
The solution set of the inequality is the infinite set
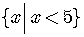       consisting of all the points to the left of 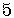, excluding .

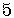B) Multiplication or Division by a Negative Number
Multiplying or dividing an inequality by a negative quantities changes
the direction of the inequality.
Look at
     .
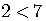Multiply both sides by a positive number.
     
            

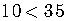
The relation was 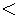   before the multiplication and remained  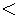  after
the multiplication by a positive number.

Now multiply both sides by a negative number.
     
              

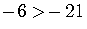
The relation was 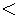before the multiplication and after
the multiplication by a negative number.
If the relation was    before the multiplication, it would be 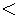   after
the multiplication by a negative number.

This change in the direction of the inequality happens ONLY
when you multiply or divide by a negative number.


Inequality with two Sides
Solve
                      .
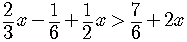If we want to get rid of the fractions, multiply the inequality
by the lowest common denominator of the fractions, .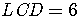

     
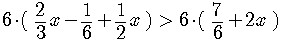
There is no change in the direction of the inequality
because we multiplied by a positive number.

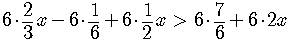          by the distributive property.

            

                     

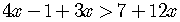
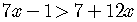
Let's start moving the 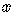, all to the left side of the inequality.

          

                   

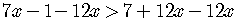
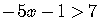
Now, let's move all the numbers to the right side.

          

                        
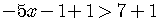
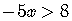
To isolate 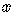  , divide both sides of the inequality by the factor  .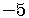
This division by a negative number changes the direction of the inequality.

                     

                         

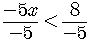
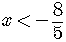
To put the answer in final form we must write it using set-builder notation.

                

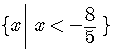
This is read: The set of all 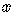  such that 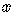   is less than   .
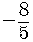The vertical slash translates as "such that".

See Examples 3 - 4, pages 103 - 104.


Inequality with Three Sides
Solve
           .

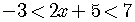As usual, the goal is to isolate the variable .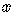
Work at the same time on all side sides - left, middle, and right - of the inequality.

     

                  

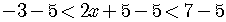
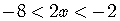
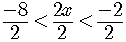                      Dividing by a positive number,
                                 so there is no change in the direction of the inequality.
                    


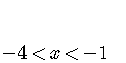
The final answer always is given in set-builder notation,
           .

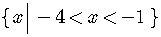See Example 5 - 6, pages 105 - 106.


                      top
                      next     Absolute Value in Equations and Inequalities