Polynomial and Rational Inequalities

The method, illustrated in the following examples, applies to all polynomial
and rational inequalities.

Polynomial Inequalities
Solve
     .

Get on ones of the inequality. Set the polynomial equal to .
Solve the resulting equation to find the x-intercepts of the polynomial.
In our problem, is already on one side of the inequality.

Look at the graph of   .
                               
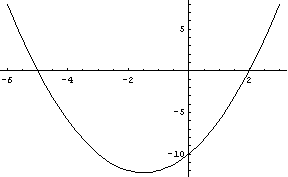
The graph of the function is displayed only to motivate what we are going
to do, so we can see what is going on. It is not a step in the method itself.

Any point on the plane is given by two coordinates, the x-coordinate giving
the horizontal displacement of the point and the y-coordinate giving the vertical
displacement of the point,
     .
To find the x-intercept (where the graph intersects the x-axis) of the function
      ,
we set
      .
We must solve the equation
      .
Factor the left side, so we can use the Zero Product Principle.
     
     
and
      
The x-intercepts are the points    and   .

Look at the points indicated on the graph above.
For all values of   , the corresponding points on the graph
are all above the x-axis, their vertical displacements from the x-axis
are positive :
For points    on the graph,
                                                        implies   .

For all values of    that lie between the x-intercepts,   ,
the corresponding points on the graph are all below the x-axis, their vertical
displacements from the x-axis are negative :

                                                  implies   .

For all values of     , the corresponding points on the graph are all above
the x-axis, their vertical displacements from the x-axis are positive :

                                                            implies    .

All these information can be summarized by drawing a horizontal number line
on which the x-intercepts are indicated as well as the signs of the coordinate
on each subinterval of the line.



We see that the x-intercepts, -5 and 2, divide the number line into three subintervals.


Now, let's get back to the method itself after this attempt at motivating it :
To determine the sign of   in each of these subintervals, it is not necessary
to draw the graph. All we have to do is find the value of      at a single,
arbitrary point in each of these subintervals.
If the value of     is positive (negative) at that point, it is positive (negative)
for all values of     in the subinterval.

Okay, let's see how these works:
In the subinterval    , choose   .
Any value of will do, it is totally arbitrary.

     
          

        is positive at this one point, so it is positive for all  
 in the subinterval  .
      Why?
Well, if   were negative at some other point in the subinterval, that means
that the graph at that point lies below the x-axis and so the graph must intersect
the x-axis at some point in the subinterval, have another x-intercept.
     But wait - !
We found all the x-intercepts of the graph. There are only two of them,
at    and   . There can not be a third x-intercept!
Conclusion:
If the graph is above the x-axis (  ) in the subinterval, it forever must remain
above the x-axis (   ) in the subinterval.
Similarly, if it is below the x-axis (  ) in the subinterval, it must forever remain
below the x-axis ( ) in the subinterval.

To finish the problem, just look at the number line.

The problem was to find the values of for which
                  ( ).
Less than zero means negative.
Where do you see the negative sign on the line?
The middle subinterval, that is the answer. The solution set is
           .
At the endpoints   and   , the value of   
so these endpoints are not included in the solution set.

If the problem were
               ( ),
to find the answer just look at the number line.
Where do you see the positive sign?
The subintervals on the left and on the right.
The solution set is
         .

At the endpoints and , the value of  
so these endpoints are included in the solution set.

An outline of the method is on page 155.
See the example on pages 153 - 154, and Example 1, pages 155 - 157.


Rational Inequalities
To solve a polynomial inequality,  ,
we solve the equation
       .

To solve a rational inequality,   ,
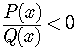we must solve the equations
     
and
      .

Note that in both cases we must put the inequality in standard form,
namely, one side must be .


Solve
     .

First, put it in standard form.