Basic
Tools: Circles
A mathematical relationship
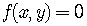
is often geometrically visualized (graphed) by plotting
an appropriate number of points,
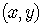 ,
,
on the rectangular Cartesian coordinate system.
How many points must be plotted?
The honest answer is, as many points as necessary for us to be perfectly
sure we know what the graph looks like. Two points may be enough, or
three points, or a hundred points or ...?
See Examples 1 -2, pages 176 - 178.
The task of graphing is easier if a graph is symmetric with respect to the x-axis
or the y-axis or the origin.
See Figure 8 on page 179, and Example 3, pages 180 - 182.
The Distance Between Two Points 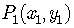 and
and 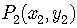 is
is
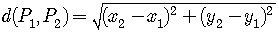 .
.
See Example 4, page 183.
Circles
How might we define a circle to a person blind from birth?
It is not enough to say it is round. Shapes like a pear, apple, or football
are round but not circles. A definition precise enough so we can get a
mathematical equation from it is, a circle is the path of a point moving so
that the point is always the same distance from a fixed point called the
center. The "same distance" is called the radius of the circle.
The circle is composed of an infinite number of points.
Let the center 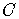 be given by the coordinates
be given by the coordinates 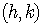 .
.
Let 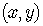 be any other
point on the circle.
be any other
point on the circle.
The distance between 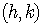 and
and 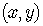 is just the
radius,
is just the
radius, 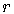 , of the
circle
, of the
circle
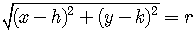 .
.
To get the standard form of the equation of the circle, square both sides
of the equation,
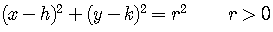 .
.
If the center is at the origin 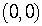 of the coordinate system, the equation becomes
of the coordinate system, the equation becomes
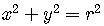 .
.
Single Point
Note that if 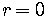 , the graph consists of the single point
, the graph consists of the single point 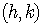 .
.
No Graph
If 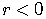 , there is no graph at all since the solutions of
, there is no graph at all since the solutions of
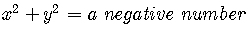
involve imaginary numbers which can not be graphed
on the Cartesian coordinate system.
For example,
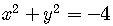 .
.
If 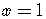 ,
then
,
then
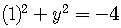
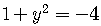
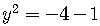
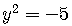
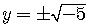
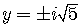 an imaginary number.
an imaginary number.
When the equation of a circle is given in standard form,
we can simply read out the coordinates of the center and the radius.
For example,
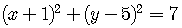 .
.
Do a simple rewrite so it looks exactly like
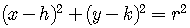 .
.
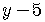 is already in the form
is already in the form 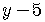 ,
,
so the y-coordinate of the center is 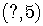 .
.
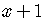 is not in the form
is not in the form 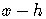 ,
but we can rewrite
,
but we can rewrite
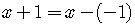 ,
so the center is at
,
so the center is at 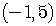 .
.
The number on the right side of the standard form is not the radius
but the square of the radius, 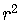 .
.
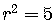
The radius is positive, so 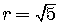 .
.
Throw away the negative solution of the quadratic equation.
When the equation of a circle is not given in standard form,
use the process of completing the squares to rewrite the equation in standard
form.
For example,
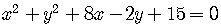 .
.
Group the 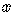 and
the
and
the 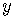 , and transpose
the constant
, and transpose
the constant
to the other side of the equation,
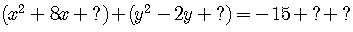
Now complete the squares for the 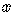 terms and the
terms and the 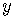 terms.
terms.
For the 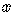 , take
one-half of the coefficient of the linear term
, take
one-half of the coefficient of the linear term
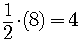
and square it, 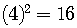 is the number to add inside the parentheses
is the number to add inside the parentheses
around the 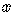 terms
in order to get a perfect square trinomial
terms
in order to get a perfect square trinomial
(that is the goal of completing the squares).
Remember to add the 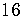 to both sides of the equation!
to both sides of the equation!
Do the same thing for the 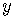 terms.
terms.
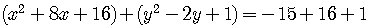
This the same as
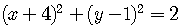 .
.
The center is at
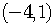 .
.
The radius is
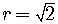 .
.
See Examples 5 - 6, pages 185 - 186.